МІНІСТЕРСТВО ОСВІТИ І НАУКИ,

МОЛОДІ ТА СПОРТУ УКРАЇНИ

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ

Лабораторний практикум з дисципліни

«Прикладна математика»

для студентів напряму підготовки

„Видавничо-поліграфічна справа”

денної форми навчання

Укладачі: Макарова Г. В.

Відповідальний за випуск Малярець Л. М.

Харків, Вид. ХНЕУ, 2011

Затверджено на засіданні кафедри вищої математики.

Протокол №8 від 28.03.2011 р.

Лабораторний практикум з дисципліни «Прикладна математика» для студентів напряму підготовки „Видавничо-поліграфічна справа” денної форми навчання / Укл. Г. В. Макарова – Харків: Вид. ХНЕУ, 2011. – 94 с. (Укр. мов.)

Пропонується цикл практичних лабораторних робіт на персональних комп’ютерах в середовищах МАТLAB та MS Excel з дисципліни «Прикладна математика». Рекомендовано для студентів напряму підготовки „Видавничо-поліграфічна справа” денної форми навчання

 Харківський державний

економічний університет, 2011

Вступ

Дисципліна „Прикладна математика” є нормативною дисципліною природничо-наукового циклу, яка є важливою складовою структурно-логічної схеми, передбаченої освітньо-професійною програмою підготовки напряму „Видавничо-поліграфічна справа”.

Метою вивчення даної дисципліни є формування в майбутніх спеціалістів необхідних знань та навичок щодо розв’язання теоретичних і практичних задач з технології електронних мультимедійних видань та комп’ютеризованих технологій і систем поліграфічних виробництв, побудови математичних моделей цих задач та їх математичного дослідження. Цієї меті служить включеня в курс «Прикладна математика» лабораторних практичних занять, які проводяться на ОЦ з використанням різних пакетів прикладних програм, таких як МАТLAB, MathCAD та MS Excel.

Комп’ютеризація навчального процесу підготовки фахівців є важливою складовою умовою досягнення майбутніми магістрами та спеціалістами з вищою освітою високого рівня професіоналізму та загального рівня освіти.

Метою проведення занять на ПК є закріплення набутих теоретичних знань та практичних навичок, отриманих на лекційних та практичних заняттях у поєднанні з оволодінням основними засобами символьної математики середовища МАТLAB у процесі розв’язання типових задач, передбачених робочою програмою.

Структура розробленого практикуму така:

• тема лабораторного практичного заняття;

• мета його проведення;

• порядок виконання роботи;

• методичні рекомендації (вони включають постановку задач, алгоритми іх розв’язання та демонстраційні приклади);

• питання для захисту роботи;

• варіанти для самостійної роботи студента, які треба виконати у відповідності до умов даної лабораторної роботи.

1. Лабораторна практична робота №1

Тема: Ознайомлення з середовищем MatLab.

Основні функції MatLab. Абсолютна та відносна погрішності

1. Мета роботи

Сформувати у студентів знання, уміння і навички роботи з пакетом прикладних програм MatLab та розглянути методи роботи цього пакету з наближеними числами при застосуванні формул погрішностей елементарних дій і функцій.

1.2. Порядок виконання роботи

1. Вивчити теоретичну частину (лекційний матеріал) : означення абсолютної та відносної погрішностей, способи їх розрахунку та основні положення роботи з пакетом прикладних програм MatLab. Виконати завдання, що відповідають номерові Вашого варіанта.

2. Оформите звіт по лабораторній роботі, що повинний містити:

• Формулювання завдання (варіант завдання вибирається відповідно до номера в журналі).

• Роздруківку послідовності виконання команд у програмному середовищі MatLab, що відповідає своєму завданню.

• Результати виконання програми (у разі потреби варто привести проміжні результати, а також графіки)

• Висновки (інтерпритація отриманих результатів).

1.3. Методичні рекомендації

1.3.1. Знайомство із середовищем MatLab

Запуск MatLab приводить до відкриття робочого середовища, зображеного на рис. 1.1. (виражаю свою вдячність за дані наробітки Резніку Е. В. та Тижненко О. Г.)

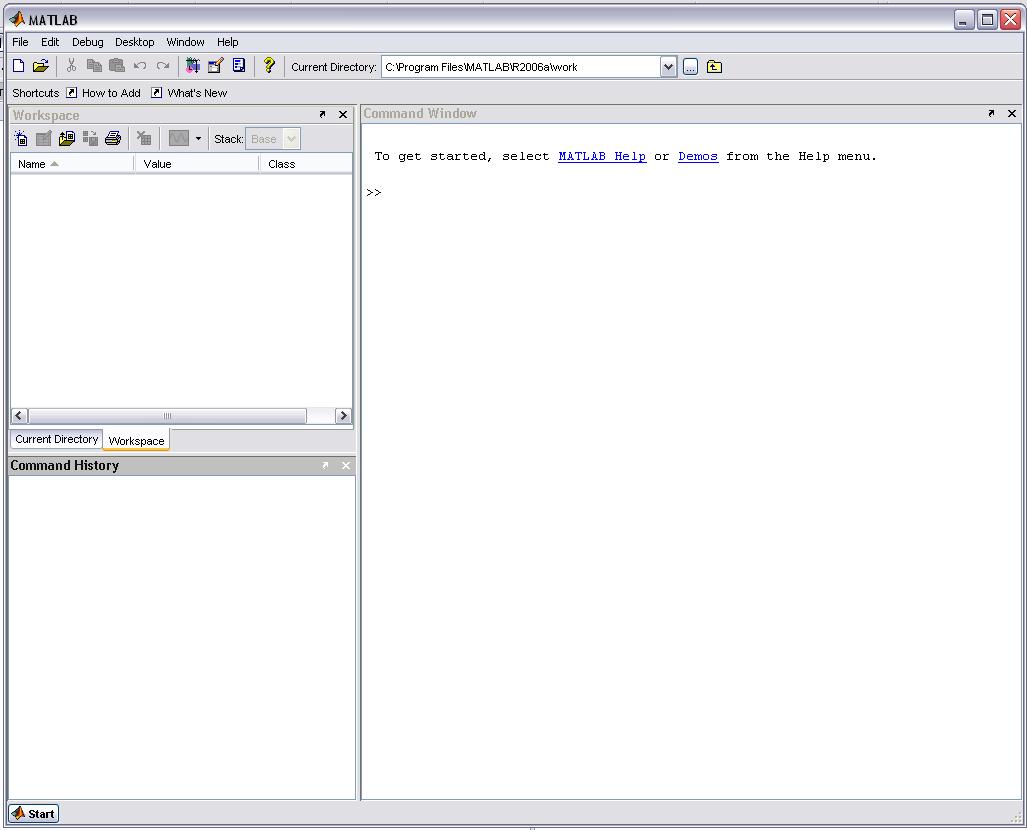
Рис.1.1. Вікно робочого середовища MatLab

Робоче середовище MatLab включає в себе наступні елементи:

• меню;

• панель інструментів з кнопками й списками, що розкриваються;

• вікно з вкладками Launch Pad (засіб для отримання швидкого доступу до різних модулів пакетів розширення (Toolboxes) MatLab), Command Window(усі розрахунки виконуються у ньому), Current Directory (використовується для встанови поточної директорії), Workspace(зберігаються змінні, що були отримані під час розрахунків) Command History (використовується для розгляду та повторного виклику раніш введених команд);

• рядок стану.

За бажанням користувача вид середовища може бути змінений за допомогою пункту меню Вид (View). Усі команди слід набирати у командному вікні, яке містить командний рядок. Командний рядок починається з символу ">>", що позначає запрошення до вводу команди.

1.3.2. Розрахунки в MatLab

Обчислення математичних виразів у системі MatLab проводяться за допомогою елементарних функцій (таблиця 1.1).

Таблиця 1.1. Внутрішні елементарні функції MatLab

Тригонометричні функції	sin(x), cos(x), tan(x), cot(x) , sec(x), csc(x) – синус, косинус, тангенс, котангенс, секанс
Зворотні тригонометричні функції	asin(x), acos(x), atan(x), acot(x), asec(x), acsc(x) – арксинус, арккосинус, аркангенс, арккотангенс, арксеканс, арккосеканс змінної x
Гіперболічні функції	sinh(x), cosh(x), tanh(x), coth(x), sech(x), csch(x) – гіперболічні синус, косинус, тангенс, котангенс, секанс, косеканс змінної x.
Зворотні гіперболічні функції	asinh(x), acosh(x), atanh(x), acoth(x), asech(x), acsch(x) – гіперболічні арксинус, арккосинус, аркангенс, арккотангенс, арксеканс, арккосеканс змінної x.
Експоненц. ф-ція	exp(x)
Логарифми	log(x), log10(x), log2(x) – логарифми натуральний, десятинний та за основою два відповідно змінної x . Якщо потрібно обчислити логарифм за іншою основою, то можна скористатися формулою переходу до нової основи: . За нову основу b можна взяти основу натурального логарифма. Тому для обчислення можна використати наступний вираз: log(x)/log(a)
Обчислення квадратного кореня	sqrt(x)
Функції для роботи з комплексними числами	- abs(z), angle(z) – модуль та аргумент(в радіанах від - до ) комплексного числа z. - complex(a,b) – конструює комплексне число по його дійсній (a) та мнимій (b) частинах (або можна записати: z=a+i*b ) - conj(z)– повертає комплексно-спряжене число - imag(z)– повертає мниму частину комплексного числа z - real(z)– повертає дійсну частину комплексного числа z
Округлення і залишок від ділення	- fix – округлення до найближчого цілого за напрямком до 0 - floor, ceil - округлення до найближчого цілого за напрямком до - або + - round – округлення до найближчого цілого - mod(a,b) - залишок від цілочисленного ділення a на b (із знаком) - sign - функція знаку числа (повертає -1 для від’ємних чисел, 1 для невід’ємних та 0 для 0)

Приклади використання операцій та функцій системи MatLab

>>sin(3*pi)+cos(pi/2)/tan(pi/3)

ans =

4.0275e-016

>>exp(-2.5)*log(11.3)^0.3-sqrt((sin(2.45*pi)+cos(3.78*pi))/tan(3.3))

ans =

-3.2105

Набір будь-якої команди чи виразу повинен закінчуватись натискуванням клавіші <Enter>, для того щоб ця команда була виконана. Відповідь виводиться у командне вікно. Слід також указати на одну особливість при наборі команд у командному рядку, а саме про випадок, коли математичний вираз виявляється настільки довгим, що для нього не вистачає одного рядка. Тоді вираз може бути перенесеним в новий рядок за допомогою знака багатокрапки "..." (3 чи більше), наприклад:

>>sin(2*pi/3)-log2(16)+(123-sqrt(196))/(2^3-cos(3*pi/7)^(-1/3)) ...

+log(1+exp(-2))

ans =

14.1589

Якщо не має необхідності виводити результат у командне вікно, то відповідну команду слід закінчити символом крапки з комою(;).

>>sin(2*pi/3)-log2(16)+(123-sqrt(196))/(2^3-cos(3*pi/7)^(-1/3)) ...

+log(1+exp(-2));