Завдання третього рівня:

Завдання 1.

Написати програму, яка визначає, чи належить точка з координатами (x,y) заштрихованій області D, зображеній на заданому малюнку (номер малюнку співпадає з номером варіанту).

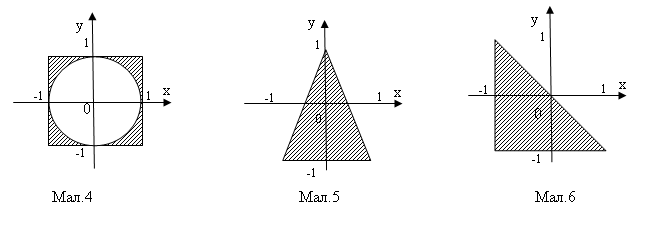
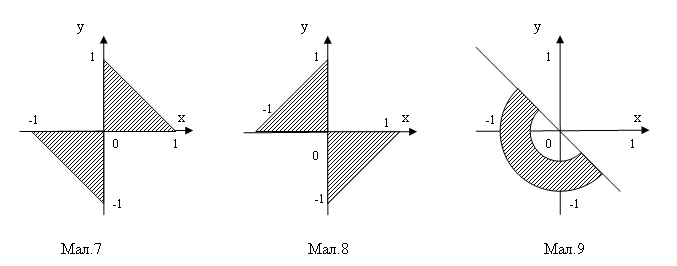
Завдання 2.

1. Визначити кількість і суму цифр у введеному натуральному числі. Введене натуральне число вивести як єдине число, розташувавши цифри в зворотньому порядку.

2. Надрукувати в зростаючому порядку всі тризначні числа, в десятковому записі яких немає однакових цифр.

3. Скласти програму, яка перевіряє чи є дане число досконалим. Досконалим вважається число, яке дорівнює сумі всіх своїх дільників, що не перевищують самого числа. Наприклад, 6=1+2+3.

4. Дано натуральне число N. Визначити, чи є воно автоморфним. Автоморфне число N дорівнює останнім розрядам квадрату цього числа. Наприклад, числа 5, 6, 25, оскільки 5²=25, 6²=36, 25²=625.

5. Перевірити, чи є введене ціле додатнє число простим. Простим називається число, яке має тільки два дільники (одиницю і саме це число).

6. Перевірити, чи є два введених цілих додатних числа взаємно простими. Взаємно простими називаються числа, найбільший загальний дільник яких дорівнює 1.

7. Вивести всі дільники заданого натурального числа.

8. Натуральне число з n цифр є числом Армстронга, якщо сума його цифр, зведених в n-ю ступінь, дорівнює самому числу (як, наприклад, 153= 1³+5³+3³). Отримати всі числа Армстронга, що складаються з двох, трьох і чотирьох цифр.

9. Знайти найбільший загальний дільник і найменше загальне кратне двох введених натуральних чисел.

10. Знайти число з даного проміжку, яке дорівнює кубу суми всіх своїх цифр. Наприклад, 512=(5+1+2)^3.

11. Дано натуральне число n. Отримати всі пифагорові трійки натуральних чисел, кожне з яких не перевищує n, тобто всі такі трійки натуральних чисел а, b, с, що а²+b²=с² (а≤b≤с≤n).

12. Дано натуральне число N. Визначити, чи є воно паліндромом. Число-паліндром можна читати справа наліво і зліва направо однаково. Наприклад, 4; 88; 121; 767767.

13. Серед всіх шестизначних чисел перевірити і порахувати кількість “щасливих” квитків.

Завдання 3.

Скласти програму для обчислення суми нескінченного ряду з погрішністю ε=10^-3

.

Процес підсумовування припиняється, як тільки виконається нерівність ε, де -поточний член ряду підсумовування, а - попередній член ряду.

Номер варіанту	Сума ряду	Точність обчислень
1.		ε=10-3
2.		ε=10-3
3.		ε=10-4
4.		ε=10-4
5.		ε=10-3
6.		ε=10-3
7.		ε=10-3
8.		ε=10-3
9.		ε=10-3
10.		ε=10-3
11.		ε=10-4
12.		ε=10-4
13.		ε=10-4