
3.2. Алгебраїчний метод
Суть
цього методу полягає в послідовному
застосуванні основних аксіом і законів
булевої алгебри. Найчастіше для спрощення
формул використовуються закони:
склеювання![]() та поглинання
та поглинання
![]() ,
де
,
де
![]() – змінна в прямій або інверсній формі.
– змінна в прямій або інверсній формі.
Приклад 3.1. Мінімізувати функцію
 ,
,
де нижні індекси показують номери доданків, які являють собою мінтерми.
Розв’язання. Легко бачити, що можна виконати операцію склеювання таких пар мінтермів: 1 і 2 за змінною А; 2 і 3 за змінною С; 2 і 4 за змінною В; 3 і 5 за змінною В; 4 і 5 за змінною С;
В
результаті виконання операцій склеювання
отримаємо скорочену формулу![]() ,
в якій можна провести склеювання
доданків: 2 і 5 за змінною В;
3 і 4 за змінною С.
При цьому отримаємо формулу
,
в якій можна провести склеювання
доданків: 2 і 5 за змінною В;
3 і 4 за змінною С.
При цьому отримаємо формулу
![]() ,
яка містить два одинакові доданки, що
дає можливість остаточно записати
функцію у вигляді
,
яка містить два одинакові доданки, що
дає можливість остаточно записати
функцію у вигляді
![]() .
.
Приклад
3.2.
Мінімізувати функцію
![]() ,
задану
в ДНФ.
,
задану
в ДНФ.
Розв’язання.
Для розв’язання поставленої задачі
доцільно спочатку перетворити до ДДНФ.
Скориставшись аксіомою
![]() ,
запишемо:
,
запишемо:
![]() .
.
Після
розкриття дужок та врахування аксіоми
![]() ,
дістанемо ДДНФ вигляду:
,
дістанемо ДДНФ вигляду:
 .
.
Застосовуючи до одержаних мінтермів закон склеювання дістанемо наступні дві мінімальні форми:
якщо склеїмо 2-й з 3-м за змінною С, 1-й з 5-м за змінною А та 4-й з 6-м за змінною В, то
 ;
;якщо склеїмо 2-й з 6-м за змінною А, 1-й з 3-м за змінною В та 4-й з 5-м за змінною С, то
 .
.
Одержані мінімальні форми є мінімальними за всіма вище введеними критеріями простоти.
3.3. Метод Квайна
При
мінімізації за методом Квайна в базисі
![]() вважають, що функція задана в ДНФ і
використовується поняття первинної
або простої імпліканти .
вважають, що функція задана в ДНФ і
використовується поняття первинної
або простої імпліканти .
Метод
Квайна полягає в застосуванні до
імплікант, які входять в ДНФ функції f
закону поглинання ![]() .
.
Використовуючи операцію поглинання вдається знизити ранг термів. Ця процедура продовжується до тих пір, поки не залишиться жодного терму, який допускає поглинання з яким-небудь іншим термом. Терм над яким було здійснено поглинання відмічаються. Не відмічені терми представляють собою первинні імпліканти.
Метод Квайна виконується в декілька етапів.
Продемонструємо метод Квайна на прикладах.
Приклад
3.3.
Нехай потрібно мінімізувати функцію
![]()
Застосовуючи
операцію склеювання дістанемо: ![]()
Тут за допомогою нижніх індексів вказані номери імплікант, в результаті склеювання яких, одержується відповідна імпліканта нижчого рангу.
В
результаті таких перетворень одержимо
скорочену форму
![]() .
.
Оскільки подальше спрощення неможливе, то одержана форма є тупиковою, а отже, і мінімальною.
А тепер приступимо до реалізації методу Квайна.
Етап1. Знаходження первинних імплікант. Перш за все складається таблиця (табл. 1) і знаходяться імпліканти третього і другого рангу, тобто знижується ранг членів, які входять в ДДНФ.
Таблиця 1
-
Початкові терми





+

1


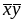
+

1
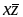
+

1
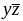
+

1
+

1
В табл.1 і нижче символом “+” позначені терми (імпліканти), до яких застосовувався закон поглинання.
Таблиця 2
-





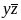
+

1

+

1
1
+

1
+
1
Після цього складається таблиця (табл. 2), яка включає всі терми, які не брали участь у поглинанні (таких немає), а також первинні імпліканти другого рангу. В загальному, складання таблиць продовжується до тих пір, поки можна застосувати закону поглинання.
Складаємо наступну таблицю, яка включає усі терми, які не підлягають поглинанню на попередніх кроках (таким термом в даному випадку є терм ), а також імпліканти 1-го рангу.
У розглядуваному прикладі можна дійти до первинних імплікант першого рангу (табл. 3).
Таблиця 3
-

1
1
В
результаті етапу 1 одержуємо дві первинні
імпліканти:
![]() і
і
![]() .
.
Етап2. Розставлення міток. Складається таблиця (табл. 4), число рядків, якої дорівнює числу первинних імплікант, а число стовпців співпадає з числом мінтермів (конституент одиниць) ДДНФ функції f. Якщо в деякий мінтерм ДДНФ входить яка-небудь із первинних імплікант, то на перетині відповідного стовпця і рядка ставиться мітка (символ “*”).
Таблиця 4
-
Первинні імпліканти
1
2
3
4
5





*
*
*
*
*
*
Етап
3. Знаходження
істотних імплікант.
Якщо
в деякому стовпці таблиці знаходиться
лише одна мітка, то первинна імпліканта
у відповідному рядку є істотною, оскільки
без неї не буде можливості одержати усю
множину заданих мінтермів. У даному
випадку такою імплікантою є
![]() .
Стовпці, які відповідають істотним
імплікантам, із таблиці викреслюються.
У даному випадку такими імплікантами
є
.
Стовпці, які відповідають істотним
імплікантам, із таблиці викреслюються.
У даному випадку такими імплікантами
є
![]() і
і
![]() .
Завдяки імплікації
в табл. 4 можна викреслити стовпці 1,2,3
5, а завдяки імплікації
– стовпець 4. Зауважимо, що в першу чергу
розглядаємо імплікацію, яка більше
покриває конституент одиниці. В результаті
такої дії приходимо до результату, коли
покриті усі конституент одиниці, а
оскільки імпліканти
і
є первинні, то можна записати мінімальну
форму у вигляді
.
Завдяки імплікації
в табл. 4 можна викреслити стовпці 1,2,3
5, а завдяки імплікації
– стовпець 4. Зауважимо, що в першу чергу
розглядаємо імплікацію, яка більше
покриває конституент одиниці. В результаті
такої дії приходимо до результату, коли
покриті усі конституент одиниці, а
оскільки імпліканти
і
є первинні, то можна записати мінімальну
форму у вигляді
![]() .
.
У загальному випадку можуть бути наступні етапи.
Етап 4. Викреслювання лишніх стовпців. Після третього етапу в результаті викреслювання стовпців може одержатись таблиця, в якій є два стовпці, в яких є мітки в однакових рядках. Тоді один з них викреслюється. Покриття конституенти одиниці стовпця, який залишився буде здійснювати відкинутий мінтерм. У випадку, якщо таких рядів більше, то викреслюються всі, крім одного.
Етап 5. Викреслювання лишніх первинних імплікант. Якщо після викреслювання стовпців на етапі 4 в таблиці появляються рядки, в яких немає жодної мітки, то первинні імпліканти, які відповідають цим рядкам, вилучаються із подальшого розгляду, оскільки вони не покривають мінтерми, які залишились для розгляду.
Етап 6. Вибір мінімального покриття. В одержаній після попередніх етапів таблиці вибирається така сукупність первинних імплікант, яка включає мітки у всіх стовпцях принаймні по одній мітці в кожному стовпці. При декількох можливих варіантах такого вибору віддається перевага варіанту покриття з мінімальним сумарним числом букв в імплікантах, які здійснюють покриття.
Приклад
3.4.
Задану
функцію від чотирьох змінних![]() ,
яка на вказаних наборах дорівнює одиниці,
мінімізувати, користуючись методом
Квайна.
,
яка на вказаних наборах дорівнює одиниці,
мінімізувати, користуючись методом
Квайна.
Етап1. Знаходження первинних імплікант. Складаємо таблиці (табл.5, 6) і знаходяться імпліканти третього і другого рангу, тобто знижується ранг членів, які входять в ДДНФ до 3 і 2.
Таблиця 5
Початкові терми
1
1
1
1
1
1
1
1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таблиця 6
Первинні імпліканти рангу
3
1
1
– +
1
– +
1
1
– +
1
1
1
– +
1
![]()
В
результаті етапу 1 одержуємо шість
первинних імпліканти:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
,
,![]() .
В табл.6 символом “+” позначено імпліканти,
які брали участь в операції склеювання.
.
В табл.6 символом “+” позначено імпліканти,
які брали участь в операції склеювання.
Етап2. Розставлення міток. Складаємо табл.7, число рядків, якої дорівнює числу первинних імплікант, а число стовпців співпадає з числом мінтермів ДДНФ функції f. Символ “*” ставиться на перетині рядка і стовпця, якщо відповідна первинна імпліканта рядка входить мінтерм стовпця.
Таблиця 7
Первинні імпліканти
1
2
3
4
5
6
7
8
Початкові терми
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Етап 3. Знаходження істотних імплікант. У даному випадку такою імплікантою є . Викресливши стовпці, які відповідають даній імпліканті, (у даному випадку такими стовпцями є 2,3,7 і 8), одержимо табл. 8, за допомогою якої будемо шукати мінімальне покриття.
Таблиця 8
Первинні імпліканти
1
4
5
6
Початкові терми
*
*
*
*
*
*
*
*
Оскільки для даного випадку етапи 4 і 5 відсутні, то переходимо до етапу 6.
Етап 6. Вибір мінімального покриття. Неважко переконатись, що мінімальне покриття дають первинні імплікант і (табл.9).
Таблиця 9
Первинні імпліканти
1
4
5
6
Початкові терми
*
*
*
*
Таким
чином, мінімальна форма заданої функції
складається з суми істотної імпліканти
(етап 3) і первинних імплікант
і
![]() (етап 6), які покривають мінтерми, що
залишилися:
(етап 6), які покривають мінтерми, що
залишилися:
![]() .
.
Приклад 3.5. Користуючись методом Квайна, мінімізувати функцію, яка задана у досконалій диз’юнктивній нормальній формі
![]() .
.
В
результаті виконання етапу 1 одержимо
табл.10, з якої одержуємо чотири первинні
імпліканти рангу 2:
,
,![]() ,
,![]() .
.
Таблиця 10
Початкові терми
![]()
![]()
![]()
Результат розставлення міток наведено в табл. 11.
Таблиця 11 Таблиця 12
3
2
*
3
*
1
2
3
4
5
1
*
*
2
*
*
3
*
*
4
*
*
Викресливши
істотні імпліканти
,![]() (етап 3), одержимо результат, який наведено
в табл.12.
(етап 3), одержимо результат, який наведено
в табл.12.
Оскільки
первинні імпліканти
![]() і
і
![]() накривають той самий мінтерм
,
то це дає можливість одержати дві
мінімальні форми:
накривають той самий мінтерм
,
то це дає можливість одержати дві
мінімальні форми:
![]() або
або
![]() .
.
Приклад
3.6.
Користуючись
методом Квайна, мінімізувати функцію
від трьох змінних, яка на наборах 0, 2, 3,
4, 5, 7 приймає значення 1, на інших – 0,
тобто
![]() .
.
В
результаті виконання етапу 1 одержимо
табл.13, з якої одержуємо шість первинні
імпліканти рангу 2:
,
,![]() ,
,![]() ,
,![]() ,
.
,
.
Таблиця 13
Початкові терми
1
1
1
1
1
1
![]()
![]()
![]()
![]()
![]()
![]()
Результат розставлення міток наведено в табл. 14.
Таблиця 14
*
*
*
*
*
*
*
*
*
*
*
*
Неважко переконатись, що мінімальне покриття (етап 6) можна виконати двома способами, наведеними в таблицях 15, 16
Таблиця 15
*
*
*
*
*
*
Таблиця 16
*
*
*
*
*
*
З таблиць 15, 16 можна записати дві мінімальні форми:
![]() і
і
![]() .
.
