КОМП’ЮТЕРНА ЛОГІКА

Розділ 3. МІНІМІЗАЦІЯ ЛОГІЧНИХ ФУНКЦІЙ

3.1. Основні поняття та означення

З попередніх розділів відомо, що логічну схему, яка реалізовує задану логічну функцію можна побудувати безпосередньо за допомогою логічного виразу, поданого у вигляді ДДНФ або ДКНФ. Однак, одержана при цьому схема, як правило, не є оптимальною з точки зору її практичної реалізації, тобто містить елементи, які можна виключити при синтезі схеми.

Рис. 3.1

а)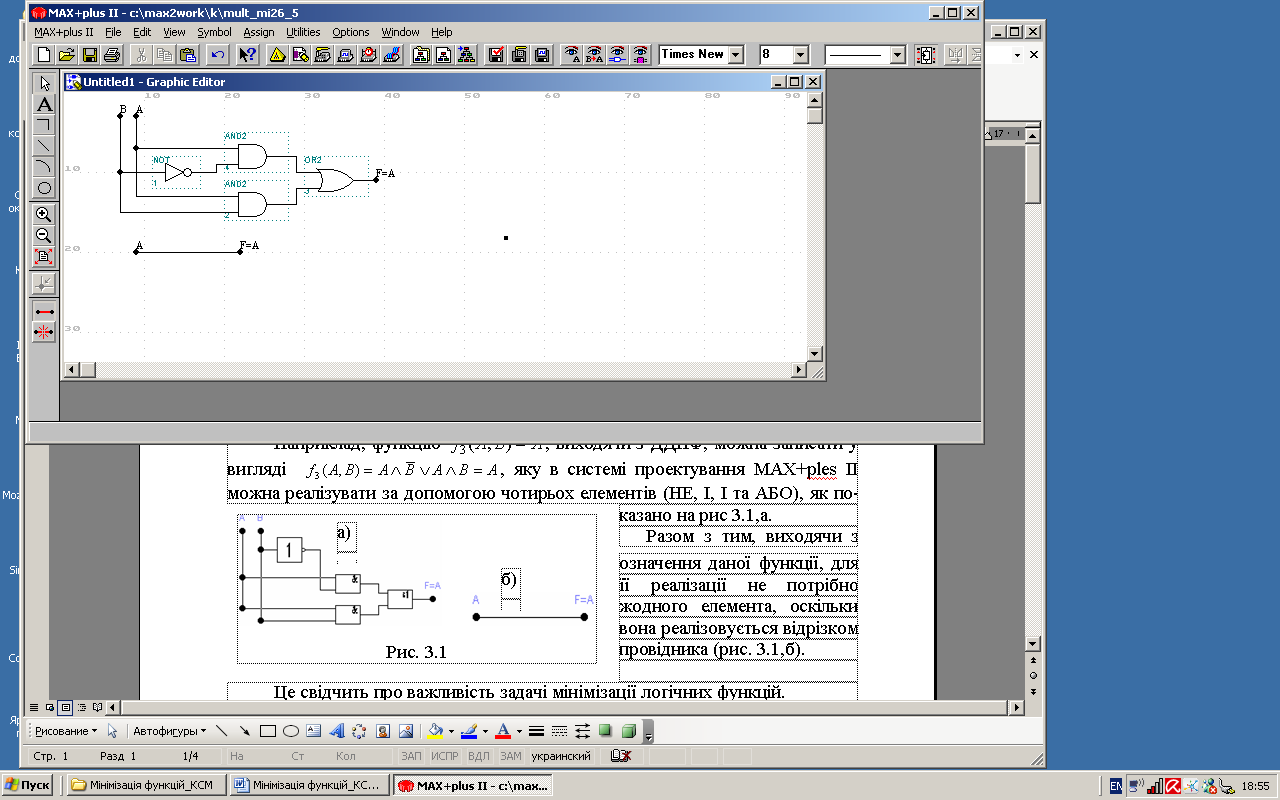

Наприклад, функцію , виходячи з ДДНФ, можна записати у вигляді , яку в системі проектування MAX+ples II можна реалізувати за допомогою чотирьох елементів (НЕ, І, І та АБО), як показано на рис 3.1,а.

Р

б)

азом з тим, виходячи з означення даної функції, для її реалізації не потрібно жодного елемента, оскільки вона реалізо-вується відріз­ком провідника (рис. 3.1,б). Це свідчить про важли­вість задачі мінімізації логічних функцій.

Метою мінімізації логічних функцій є спрощення комбіна-ційних схем, які реалізовують ці логічні функції. Мінімізацію функцій можна виконувати у різних алгебрах. Ми займемося вивченням методів знаходження мінімальних форм функцій, які задані в диз’юнктивних формах булевої алгебри, оскільки на практиці вони більш поширені.

У загальному випадку мінімізацією логічної функції прийнято називати процес відшукання найменшого за складністю аналітичного зображення даної функції у вигляді суперпозиції функцій, які належать деякій функціонально повній системі.

Методи мінімізації розробляються стосовно кожної функціонально повної системи елементарних логічних функцій. Найдокладніше такі методи розроблено для випадку, коли функціонально повна система елементарних логічних функцій складається з диз’юнкції, кон’юнкції та заперечення. При цьому мінімізація логічної функції зводиться до визначення такої її форми, яка має найменший індекс (коефіцієнт) простоти, що характеризує складність ДНФ.

Індексом простоти зображення функції у вигляді ДНФ (ДКФ) називається таке найменше число L, для якого існує формула, що зображає дану функцію і має точно L відповідних елементів, які покладено в основу мінімізації.

Найчастіше вживаються такі типи індексів простоти:

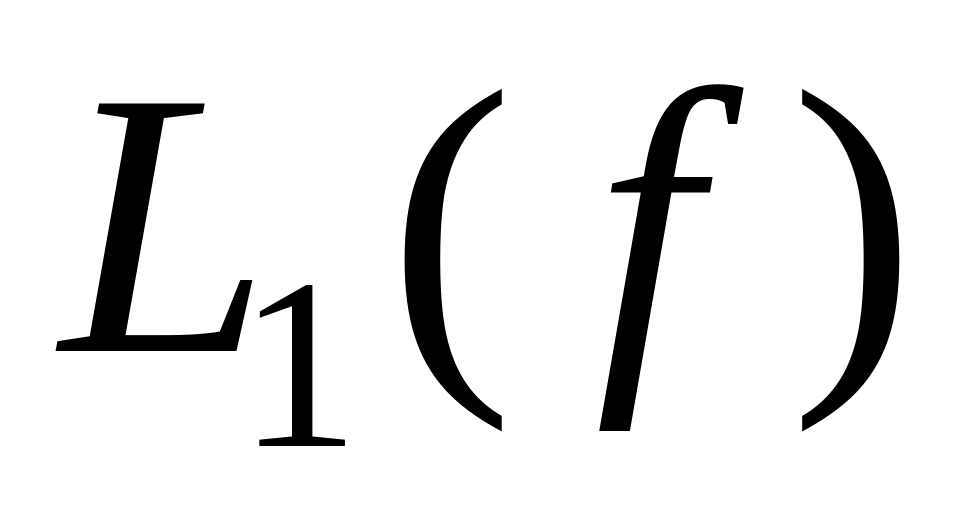• – сумарна кількість букв, (а не змінних), що до неї входять;

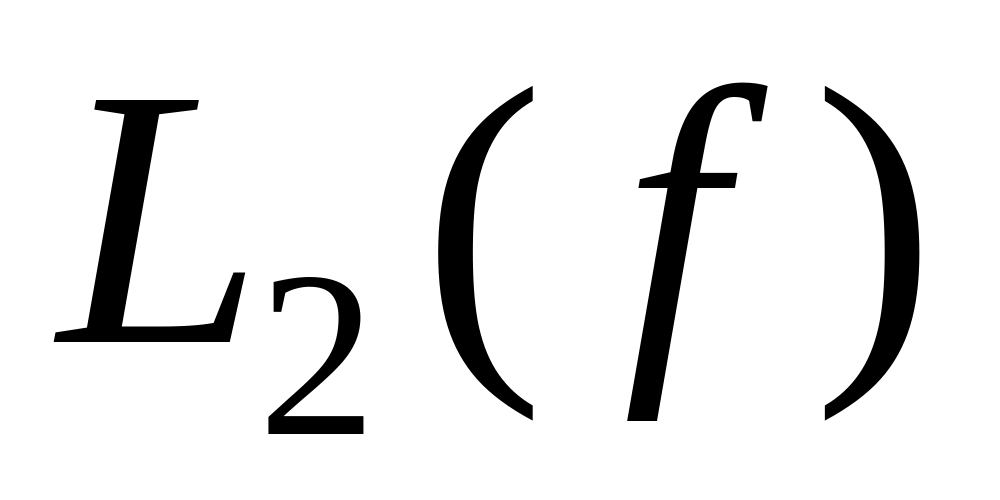• – число елементів диз’юнкції (кон’юнкції), що входять в формулу;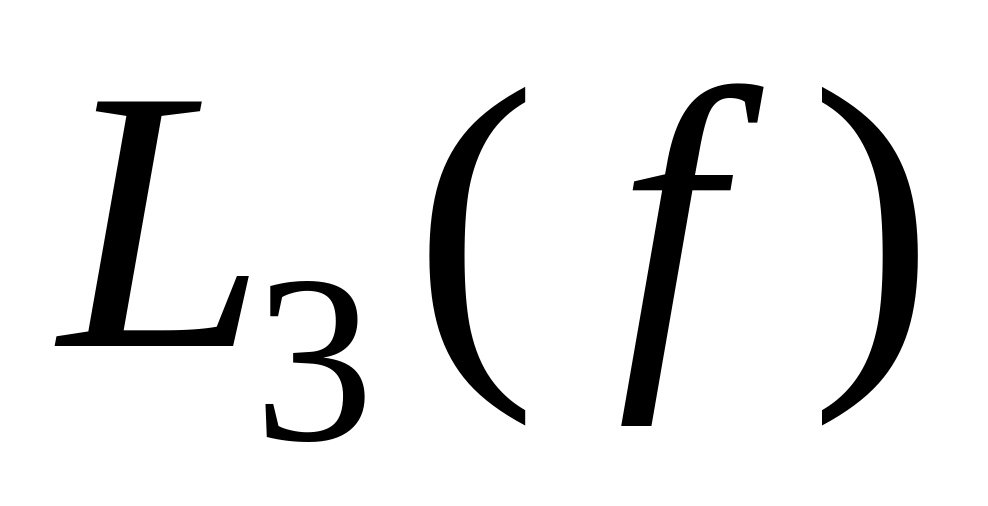

• – число символів інверсії, які зустрічаються в записі ДНФ.

Наприклад, для еквівалентних функцій

і

індекси простоти мають значення:

; ; .

З наведених індексів простоти на практиці найчастіше використовується індекс простоти , тобто найменша кількість букв.

При розв’язанні задачі мінімізації істотну роль відіграють поняття імпліканти та простої імпліканти.

Наприклад ДДНФ елементарної функції (імплікації ) має вигляд

.

Кожен із добутків (як мінтерм) накриває тільки одну одиницю функції. Проте елементарна кон’юнкція накриває одиницями дві одиниці функції у двох наборах: 00 та 01; так само елементарна кон’юнкція y – у двох наборах: 01 та 11; та y спільно накривають одиницями всі одиниці функції , яка внаслідок цього може бути подана як

.

Розглянемо дві повністю визначені функції і . Функція визначена на множині одиничних наборів і множині нульових наборів , а функція визначена на множині одиничних наборів .

Логічна функція називається імплікантою логічної функції , якщо множина одиничних наборів функції збігається або є підмножиною множини одиничних наборів функції , тобто .

Легко переконатись, що логічна функція є імплікантою функції

,

оскільки множину складають набори 011 і 111, які входять у множину 000, 001, 011, 111.

Простою імплікантою функції f називається будь-яка елементарна кон’юнкція g, яка є імплікантою цієї функції та має ту властивість, що ніяка її власна частина уже не є імплікантою даної функції.

Наприклад, для вище наведеної функції f, функція є простою імплікантою, оскільки ні y, ні z, які є її частинами, не є імплікантами. Справді, на множині наборів функції від трьох змінних, елементарна кон’юнкція y, приймає значення 1 на наборах: 010, 011, 110, 111, два із яких 010 і 110, не входять в множину одиничних значень функції f. Аналогічні висновки можна зробити відносно елементарної кон’юнкції z.

З визначення імпліканти випливає, що диз’юнкція будь-якого скінченого числа імплікант функції f є також імплікантою функції f.

Якщо при цьому імпліканти сукупно накривають усі одиниці функції f, то має місце рівність . Таку систему імплікант прийнято називати повною.

Диз’юнкцію всіх простих імплікант логічної функції називається скороченою диз’юнктивною нормальною формою СДНФ. Наприклад, для логічної функції

простими імплікантами є: ; ; , а СДНФ цієї функції має вигляд

.

Знаходження скорочених ДНФ є першим етапом знаходження мінімальних форм булевих функцій. Як уже відмічалось, в скорочену ДНФ входять усі прості імпліканти булевої функції. Іноді із скороченої ДНФ можна вилучити одну або декілька простих імплікант, не порушуючи умови еквівалентності вихідній булеві функції. Такі прості імпліканти називаються лишніми. Вилучення лишніх простих імплікант із скороченої ДНФ – другий етап мінімізації.

Система простих імплікант логічної функції називається зведеною, якщо ця система повна, а будь-яка її частина є неповною системою імплікант цієї функції.

Диз’юнкцію простих імплікант, які складають зведену систему імплікант логічної функції, називається її тупиковою диз’юнктивною нормальною формою – ТДНФ.

Наприклад, для логічної функції

ТДНФ має вигляд

.

Логічна функція може бути подана однією або декількома ТДНФ.

Мінімальною диз’юнктивною нормальною формою МДНФ функції f називається така ДНФ, яка зображає дану функцію і містить найменшу кількість букв порівняно з усі іншими еквівалентними їй ДНФ. Побудова тупикових і знаходження мінімальних ДНФ є третім етапом мінімізації.

Зауважимо, що для розглянутої вище функції МДНФ співпадає з ТДНФ.

Слід відмітити, що існують функції, які мають декілька мінімальних форм.

Таким чином, у загальному випадку, схема мінімізації логічних функцій складається з таких етапів: знаходження простих імплікант, побудови скороченої ДНФ функції, побудові тупикових ДНФ, з яких вибираються мінімальні.

Розглянемо ряд методів, які дають можливість виконати мінімізацію логічної функції за критерієм .