1. Определение главных компонент

Будем предполагать, что исследуемые наблюдения X₁, Х₂, ..., ,... Х_n извлечены из некоторой р-мерной генеральной совокупности (т.е. совокупности всех мыслимых наблюдений), определяемой соот­ветствующей вероятностной мерой. Однако для приводимых здесь поня­тий из всех характеристик исследуемой генеральной совокупности су­щественное значение имеет лишь ковариационная матрица , где

Здесь a⁽ⁱ⁾ компоненты вектора a средних значений признаков x⁽ⁱ⁾. Поскольку, как легко видеть, элементы , матрицы не изменятся при замене признаков x⁽ⁱ⁾ признаками (— произвольные постоянные числа), то будем в дальнейшем считать, что вектор средних значенийа = 0, чего всегда можно добиться, рассмат­ривая в качестве исходных признаков x⁽¹⁾, x⁽²⁾, …,x^(p) не сами из­мерения (v = 1, 2, ..., п), а их отклонения от своих выборочных средних значений, т.е. полагая

где (4.1)

Назовем первой главной компонентой исследуемой генеральной совокупности наблюдений такую нормированную линейную комбина­цию p исходных признаков x⁽¹⁾, x⁽²⁾, …,x^(p),

(4.2)

(здесь , причем ), которая среди всех прочих нормированных линейных комбинаций x⁽¹⁾, x⁽²⁾, …,x^(p) обладает наибольшей дисперсией.

И вообще, i-й главной компонентой исследуемой генеральной сово­купности (i = 2,3, ..., р) будем называть такую нормированную линей­ную комбинацию р исходных признаков x⁽¹⁾, x⁽²⁾, …,x^(p),

(4.3)

которая среди всех прочих линейных нормированных комбинаций, некоррелированных со всеми предшест­вующими главными компонентами y⁽¹⁾, y⁽²⁾, …,y^(I-1) (т.е. cov (y⁽ⁱ⁾, y^(j)) = M(y⁽ⁱ⁾y^(j))) = 0 для j<i), обладает наибольшей дисперсией.

Из определения следует, что, во-первых, главные компоненты y⁽¹⁾, y⁽²⁾, …,y^(p) занумерованы в порядке убывания их дисперсий, т.е. D y⁽¹⁾ D y⁽²⁾ … D y^(p), причем легко подсчитать

(4.4)

и, во-вторых, вектор, определяющий преобразование пере­хода от x⁽¹⁾, x⁽²⁾, …,x^(p) к y⁽ⁱ⁾ является так называемым i-м собствен­ным вектором ковариационной матрицы , т.е. его компоненты l_i1 ,l_i2 ,…,l_ip определяются как нормированное решение системы уравнений

(4.5)

где — i-й по величине корень уравнения

(4.6)

Под подразумевается определитель матрицы М, под I—так назы­ваемая единичная матрица, а под  — неизвестное число. Из сопоставления (4.4), (4.5) и (4.6) вытекает, что

(4.7)

Таким образом, ковариационная матрица _Y главных компонент y⁽¹⁾, y⁽²⁾, …,y^(p) будет иметь вид

(4.8)

Опираясь на то, что преобразование

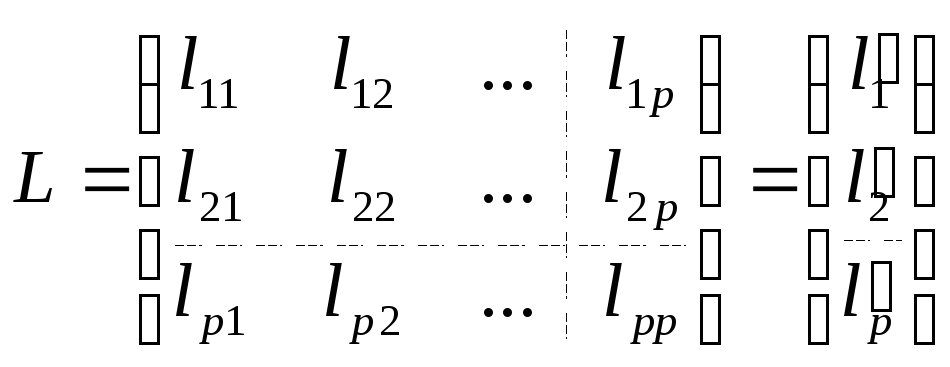
с помощью которого осуществляется переход от исходных компонент Х к главным компонентам У (Y = LX), является ортогональным, нетрудно выразить исходные переменные x⁽¹⁾, x⁽²⁾, …,x^(p) через глав­ные компоненты

(4.9)

(в матричной записи Х = L'Y), а также показать, что обоб­щенная дисперсия и сумма дисперсий (Dy⁽¹⁾ + D y⁽²⁾ + … + D y^(p)) главных компонент равны обобщенной дисперсии и сумме дисперсий (Dx⁽¹⁾ + D x⁽²⁾ + … + D x^(p)) исходных признаков.

Это дает исследователю некоторую основу, опорную точку зрения, при вынесении решения о том, сколько последних главных компонент можно без особого ущерба изъять из рассмотрения, сократив тем самым размерность исследуемого пространства.

Действительно, анализируя изменение относительной доли дис­персии

(4.10)

, вносимой пер­выми р' главными компонен­тами, в зависимости от числа этих компонент, можно разум­но определить число компо­нент, которое целесообразно оставить в рассмотрении- Так, при изменении q (р'"), изобра­женном на рис. 4.2, очевидно целесообразно было бы сокра­тить размерность пространст­ва с р = 10 до р' = 3, так как добавление всех осталь­ных семи главных компонент может повысить суммарную характеристику рассеяния не более чем на 10%.

Рис. 4.2. Изменение относительной доли суммарной дисперсии исследуемых признаков, обусловленной первыми p’ главными компонентами, в зависимости отр’(случайр=10)

Замечание 1. В ре­альных задачах точное зна­ние ковариационной матрицы  является скорее исключе­нием, чем правилом. Поэтому в тех случаях, когда  неиз­вестна, данное выше опреде­ление следует использовать применительно к выбороч­ной ковариационной матрице , элементы которой _ij подсчитываются на основании имеющихся у нас наблюдений по формуле

, (4.11)

в которой — значение i-й компоненты исследуемого вектора X, за­меренное на v-м объекте, — соответствующее центрированное на­блюдение, а — среднее значение i-ой компоненты по всем обследо­ванным объектам, т.е. .

Главные компоненты, вычисленные на основании элементов _ij, вы­борочной матрицы , называют обычно выборочными главными компо­нентами, или главными компонентами выборки, в отличие от главных компонент генеральной совокупности. В тех случаях, когда нам важно будет отличать главные компоненты выборки от главных ком­понент генеральной совокупности, мы будем снабжать первые (и все их характеристики) «крышками» сверху, например, и т. д.

Замечание 2. Использование главных компонент оказывается наиболее естественным и плодотворным в ситуациях, в которых все компоненты x⁽¹⁾, x⁽²⁾, …,x^(p) исследуемого вектора Х имеют общую физическую природу и соответственно измерены в одних и тех же еди­ницах. К таким примерам можно отнести исследование структуры бюд­жета времени индивидуумов (все x⁽ⁱ⁾ измеряются в единицах време­ни), исследование структуры потребления семей (все x⁽ⁱ⁾ измеряются в денежных единицах), исследование общего развития и умственных способностей индивидуумов с помощью специальных тестов (все x⁽ⁱ⁾ измеряются в баллах), разного рода антропологические исследования индивидуумов (все x⁽ⁱ⁾ измеряются в единицах меры длины) и т.д. Если же различные признаки x⁽¹⁾, x⁽²⁾, …,x^(p) измеряются в раз­личных единицах, то результаты исследования с помощью главных компонент будут существенно зависеть от выбора масштаба и природы единиц измерения. Поэтому в подобных ситуациях исследователь пред­варительно переходит к вспомогательным безразмерным признакам x^*(i), например, с помощью нормирующего преобразования

, (4.12)

где _ii соответствует обозначениям формул (4.1) и (4.11), а затем строит главные компоненты относительно этих вспомогательных признаков X* и их ковариационной матрицы _X, которая, как легко видеть, является одновременно выборочной корреляционной матрицей R исходных наблюдений Х.

Замечание З. В некоторых задачах оказывается полезным по­нятие так называемых обобщенных главных компонент, при определении которых оговаривают более общие (чем ) ограничения на коэффициенты l_ij, т. е. требуют, чтобы

где _ij — некоторые дополнительно введенные веса. Очевидно, при _kj = 1 при k =j и _kj = 0 при мы имеем обычное условие нор­мировки коэффициентов l_ij и обычные главные компоненты. Можно показать[29], что при такой модификации условий нормировки коэф­фициенты , с помощью которых обобщенные глав­ные компоненты у⁽ⁱ⁾ выражаются через исходные признаки x⁽¹⁾, x⁽²⁾, …,x^(p) (4.1 и 4.2), определяются как решения уравнений

(4.5')

где — i-й по величине корень уравнения

(4.6')

а матрица  = (_ij), i, j = 1,2, ..., р, — некоторая положительно оп­ределенная матрица весов. При этом, как и прежде, дисперсия обоб­щенной главной компоненты у⁽ⁱ⁾ равна , a у⁽ⁱ⁾ и у^(j) при i j взаимно некоррелированы.

Заметим, кстати, что если в качестве матрицы весов выбрать матрицу

,

то как легко показать, обобщенные компоненты (в метрике ), по­строенные по исходным признакам x⁽¹⁾, x⁽²⁾, …,x^(p) совпадут с обычны­ми компонентами, построенными по вспомогательным безразмерным (нормированным) признакам x⁽¹⁾, x⁽²⁾, …,x^(p) (4.12),

Проиллюстрируем определение главных компонент на численном примере, заимствованном из [26].

Пример 1. По данным измерений (в мм) длины (), ширины () и высоты () панциря 24 особей (п = 24) одного из видов черепах по формуле (4.11) определена выборочная ковариационная матрица

.

Решая, в соответствии с (4.6), кубичное уравнение (относительно ) вида

находим

₁=680,40; ₂=6,50; ₃=2,86.

Подставляя последовательно численные значения ₁, ₂ и ₃ в си­стему (4.5) и решая эти системы относительно неизвестных l_i = (l_i1, l_i2, l_i3)' (i = 1, 2, 3), получаем

В качестве главных компонент получаем

y⁽¹⁾=0,81x⁽¹⁾+0,50x⁽²⁾+0,31x⁽³⁾,

y⁽²⁾=0,55x⁽¹⁾+0,83x⁽²⁾+0,10x⁽³⁾,

y⁽²⁾=0,21x⁽¹⁾+0,25x⁽²⁾+0,95x⁽³⁾.

Здесь под x⁽¹⁾, x⁽²⁾ и x⁽³⁾подразумеваются в соответствии с (4.1) отклонения размеров длины (), ширины () и высоты () пан­циря от своих средних значений.

Вычисление относительной доли суммарной дисперсии, обусловлен­ной одной, двумя и тремя главными компонентами, в соответствии с формулой (4.10) дает

Отсюда можно сделать вывод, что почти вся информация о специфи­ке размеров панциря данного вида черепах содержится в одной лишь первой главной компоненте, которую и естественно использовать при соответствующей классификации исследуемых особей.