3. Порог

Под порогом подразумевается обычно то число, с которым сравни­вается расстояние между объектами (классами) или мера близости объектов для того, чтобы определить, можно ли отнести рассматривае­мые два объекта (либо объект и класс, либо два класса) к одному об­щему классу.

При конструировании классификационной процедуры порог может задаваться и как величина постоянная, не изменяющаяся в течение всей процедуры, и как величина переменная, меняющаяся по опреде­ленным правилам при переходе от одного этапа процедуры к другому (см. § 3 настоящей главы).

4. Функционалы качества разбиения на классы. Экстремальная постановка задачи кластер-анализа, связь с теорией статистического оценивания параметров

Естественно попытаться определить сравнительное качество различ­ных способов разбиения заданной совокупности элементов на классы, т. е. определить тот количественный критерий, следуя которому можно было бы предпочесть одно разбиение другому. С этой целью в поста­новку задачи кластер-анализа часто вводится понятие так называе­мого функционала качества разбиения Q(S), определенного на мно­жестве всех возможных разбиений. Функционалом он называется потому, что чаще всего разбиение S задается, вообще говоря, набором дискриминантных функций δ₁(X), δ₂(X), ... . Тогда под наилучшим разбиением S* понимается то разбиение, на котором достигается экстремум выбранного функционала качества. Надо сказать, что выбор того или иного функционала качества, как правило, осуществляется весьма произвольно и опирается скорее на эмпирические и профессио­нально-интуитивные соображения, чем на какую-либо строгую фор­мализованную систему.

Мы приведем здесь примеры наиболее распространенных функ­ционалов качества разбиения и попытаемся обосновать выбор некото­рых из них в рамках одной из моделей статистического оценивания параметров.

Пусть исследователем уже выбрана метрика р в пространстве X и пусть S=(S₁, S₂, ..., S_k) некоторое фиксированное разбиение наб­людений X₁, Х₂, ..., Х_n на заданное число k классов S_1,S₂, ..., S_k.

За функционалы качества часто берутся следующие характери­стики:

— сумма («взвешенная») внутриклассовых дисперсий

(3.11)

весьма широко используется в задачах кластер-анализа в качестве критерийной оценки разбиения [125],[11],[105],[107],[11],[76] и др.;

• сумма попарных внутриклассовых расстояний между элементами

либо

в большинстве случаев приводит к тем же наилучшим разбиениям, что и Q₁(S) и тоже используется для сравнения кластер-процедур [70],[45],[7].

— обобщенная внутриклассовая дисперсия Q₃(S) является, как известно [4, с. 231], одно из характеристик степени рассеивания многомерных наблюдений одного класса (генеральной совокупности) около своего «центра тяжести». Следуя обычным правилам вычисления ковариационной матрицы, - отдельно по наблюдениям, попавшим в какой-то один класс S,

(3.12)

где под detAпонимается «определитель матрицы А», а элементыw_qm(l) выборочной ковариационной матрицыW_l классаS_lподсчитываются по формуле:

(3.13)

где x^(ν)_i– ν-ая компонента многомерного наблюденияX_i, а-сред­нее значение ν-й компоненты, подсчитанное по наблюдениям l-го класса.

Встречается и другой вариант использования понятия обобщенной дисперсии как характеристики качества разбиения в котором операция суммирования W_lзаменена операцией умножения:

.

Как видно из формул (3.12 и 3.13), функционал Q₃(S) является средней арифметической (по всем классам) характеристикой обобщен­ной внутриклассовой дисперсии, в то время как функционал Q₄(S) пропорционален средней геометрической характеристике тех же ве­личин.

Заметим, что использование функционалов Q₃ (S) и Q₄ (S) является особенно уместным в ситуациях, при которых исследователь, в первую очередь, задается вопросом: не сосредоточены ли наблюдения, разби­тые на классы S_l S₂, ..., S_k, в пространстве размерности меньшей, чем p?

Замечание. При вероятностной модификации схем кластер-анализа соответственно видоизменится запись приведенных выше функционалов. Так, например,

,

где

или

. (3.14)

а) Общий вид функционала качества разбиения, как функции ряда параметров, характеризующих межклассовую и внутриклассовую структуру наблюдений. Зададимся вопросом: нельзя ли выделить такой достаточно полный набор величин u₁(S), u₂(S),..., характеризую­щих как межклассовую, так и внутриклассовую структуру наблюде­ний при каждом фиксированном разбиении на классы S, чтобы су­ществовала некоторая функция Q(u₁,u₂,….) от этих величин, которую мы могли бы считать в каком-то смысле универсальной характеристи­кой качества разбиения. В частности, в качестве таких величин, u₁=u₁(S),u₂=u₂(S), ... можно рассмотреть, например, некоторые числовые характеристики: степени близости элементов внутри клас­сов (u₁); степени удаленности классов друг от друга (u₂); степени «оди­наковости» распределения многомерных наблюдений внутри классов (u₃); степени равномерности распределения общего числа классифи­цируемых наблюдений п по классам (u₄).

Что касается установления общего вида функции Q(u₁,u₂,u₃,u₄), то без введения дополнительной априорной информации о наблю­дениях X_i (характере и общем виде их закона распределения внутри классов и т. п.) единственным возможным подходом в решении задачи, как нам представляется, является экспериментальное исследование. Именно с этих позиций в [12] сделана попытка опре­деления общего вида функции Q. Чтобы определить рассмотренные в этой работе величины u₁ u₂, u₃ и u₄, введем понятие кратчайшего не­замкнутого пути (КНП), соединяющего все n точек исходной сово­купности в связный неориентированный граф с минимальной суммарной длиной ребер. Под длиной ребра понимается расстояние между соот­ветствующими точками совокупности в смысле выбранной метрики. Построение такого графа можно начать с пары наиболее близких точек. Если таких пар несколько, то выбирается любая из этих пар, Пусть это будут наблюдения с номерами i₀ и j₀. Затем с помощью сравнения расстояний ρ(X_io,X_j)(j=l,2,...,n, j≠i₀, j≠j₀) и ρ(X_i0,X_q), где q=l,2,...,n,q≠i₀, q≠i₀ определяются точкии— наименее удаленные соответственно от точек и— выбирается ближайшая из них , т.е. =, если и =, если ¹. Затем точка „пристраивается" к той из точек и, к которой она ближе. Далее сравнива­ются расстояния и т. д. Очевидно, «разрубая» s ребер такого графа, мы будем делить совокупность на s+1 классов.

Пусть ρ_i(l) — i-ое ребро части графа, отнесенной к l-му классу. Всего таких ребер, как легко видеть, будет п_l — 1. И пусть — минимальное из ребер, непосредственно примыкающих к ребру ρ и относящихся к l-му классу, если таковое имеется. Занумеруем в оп­ределенном порядке граничные, разрубленные ребра λ₁, λ₂,….. λ_k-1 таким образом, чтобы имелось взаимно однозначное соответствие между номерами граничных ребер и номерами примыкающих к ним классов, за исключением одного, геометрически представленного одним из «хвостов» графа. На рис. 3.2 представлено изображение кратчайшего незамкнутого пути. Выбрасывая ребра I, II, III, полу­чаем четыре связных графа, что соответствует разбиению совокупности на четыре группы. Обозначим с помощью λ_l, одно из таких ребер l-го класса.

Рис.3.2.

Графическое изображение кратчайшего незамкнутого пути.

Теперь, следуя [12], определим величины u_iследующим образом:

, где- средняя длина реберl-го класса.

,

,

.

Эмпирический перебор различных вариантов общего вида функции Q в сочетании с анализом результатов экспертных оценок качества всевозможных разбиений привели авторов [12] к следующей формуле:

(3.15)

тде а, Ь, с и d — некоторые неотрицательные параметры, оставляющие исследователю определенную свободу выбора в каждом конкретном случае. Авторы [12] отмечали хорошее согласие своих экспериментов с экспертными оценками при a = b = c = d-= 1.

Из смысла величины u_i (i = 1, 2, 3, 4) следует, что лучшим раз­биениям соответствуют большие численные значения функционала Q, так что в данном случае требуется найти такое разбиение S*, при ко­тором Q (S*) = max_S Q(S).

Конечно, данный выбор количественного и качественного состава величин u_i и, в еще большей степени, их точное определение являются чисто эвристическими и подчас просто спорными. Это относится, в первую очередь, к величине u₃. Поэтому читатель должен принимать описанную здесь схему не как рекомендацию к универсальному ис­пользованию функционалов типа (3.15) в задачах кластер-анализа, но лишь как описание конкретного примера одного из возможных подходов при выборе функционалов качества разбиения.

б) Функционалы качества разбиения при неизвестном числе классов. В ситуациях, когда исследователю заранее не известно, на какое Число классов подразделяются исходные многомерные наблюдения Х₁, Х₂, ..., Х_п, функционалы качества разбиения Q(S) выбирают чаще всего в виде простой алгебраической комбинации (суммы, разности, произведения, отношения) двух функционалов I₁(S) и I₂(S), один из которых I₁ является убывающей (не возрастающей) функцией числа классов k и характеризует, как правило, внутриклассовый разброс наблюдений, а второй I₂ является возрастающей (неубывающей) функцией числа классов k. При этом интерпретация функционала I₂ может быть различной. Под I₂ понимается иногда и некоторая мера взаимной удаленности (близости) классов, и мера тех потерь, которые приходится нести исследователю при излишней детализации рассматриваемого массива исходных наблюдений, и величина, обратная так называемой «мере концентрации» всей структуры точек, полученной при разбиении исследуемого множества наблюдений на k классов. В [41], например, предлагается брать

,

где k(S)- число классов, получающихся при разбиенииS, а с – некоторая положительная постоянная, характеризующая потери исследователя числа классов на единицу. Другой вариант функционалов качества такого типа можно найти, например, в [10], где полагают

,

.

Здесь К (X, Y) — упомянутая выше потенциальная функция, а r(S_i, S_j) — мера близости i-го и j-го классов, основанная на потенциальной функции (3.6).

Очевидно, в первом случае мы будем искать разбиение S*, мини­мизирующее значение функционала

Q(S)=I₁(S)+I₂(S)

в то время как во втором случае требуется найти разбиение S°, которое максимизировало бы значение функционала

Q’(S)=I₁’(S)+I₂’(S)

Весьма гибкой и достаточно общей схемой, реализующей идею одновременного учета двух функционалов, нам представляется схема, предложенная А. Н. Колмогоровым (см. сноску к стр. 83). Эта схема опирается на понятия меры концентрации Z_r(S) точек, соответствую­щей разбиению S, и средней меры внутриклассового рассеяния ,характеризующей то же разбиение S.

Под мерой концентрации Z_r (S) предлагается принимать величину

где ν(X_i) — число элементов в кластере, содержащем точку Х_i, а выбор - числового параметра r находится в распоряжении исследователя и за висят от конкретных целей разбиения. При выборе r полезно иметь в виду следующие частные случаи Z_r (S):

Z_-1(S)=1/k.

где k — число различных кластеров в разбиении S;

— естественная информационная мера кон­центрации;

,

,

.

Заметим, что при любом r предложенная мера концентрации имеет минимальное значение, равное , при разбиении исследуемого множе­ства на п одноточечных кластеров и максимальное значение, равное 1, при объединении всех исходных наблюдений в один общий кластер. При конструировании и сравнении различных кластер-процедур полезно иметь в виду, что объединение двух кластеров S_l и S_m в один дает прирост меры концентрации Z₁ (S), равный

Определение средней меры внутриклассового рассеяния I_r^(К)(S) также опирается на понятие степенного среднего. В частности, полагают

, (3.19)

где под

понимается обобщенная средняя мера рассеяния, характеризующая класс S_i. Числовой параметр r здесь, как и прежде, выбирается по ус­мотрению исследователя. Полагая

где, как и прежде, S(X) — кластер, в который входит наблюдение X, a ν(X)—число элементов в кластере S(X), формулу (3.19) можно переписать в виде

. (3.20)

При конструировании и сравнении различных кластер-процедур полезно иметь в виду, что объединение двух кластеров S_l, и S_m в один дает прирост величины , непосредственно характе­ризующей среднюю меру внутриклассового рассеяния, равный

.

Очевидно, если ориентироваться на сокращение числа кластеров при наименьших потерях в отношении внутриклассового рассеи­вания, не обращая внимания на меру концентрации, то естественно объединять два кластера, для которых минимальна величина . Если же одновременно ориентироваться и на рост взвешен­ной концентрации Z₁(S), то объединение кластеров естественно под­чинить требованию минимизации величины

.

в) Формулировка экстремальных задач разбиения исходного мно­жества на классы.

Вариант 1: комбинирование функционалов качества. Требу­ется найти такое разбиение S*, для которого некоторая алгебраиче­ская комбинация функционала, характеризующего среднее внутри­классовое рассеяние (3.20), и функционала, характеризующего меру концентрации полученной структуры (3.18), достигала бы своего экстремума. В качестве примеров можно привести комбинации Q(S) и Q'(S), задаваемые формулами (3.16) и (3.17), выражения вида

(3.21)

где ,

а α и β — некоторые положительные константы, например, α=β=1.

Вариант 2: двойственная формулировка. Требуется найти разбиение S*, которое, обладая концентрацией Z_r(S*), не меньшей заданного порогового значения Z₀, давало бы наименьшее внутриклас­совое рассеяние или в двойственной подстановке: при задан­ном пороговом значении I₀ найти разбиение S* с внутриклассовым, рассеянием наибольшей концентрацией Z_r (S*).

г) Функционалы качества и необходимые условия оптимальности-разбиения. Естественно попытаться проследить, в какой мере выбор того или иного вида функционала качества определяет класс раз­биений, в котором следует искать оптимальное. Приведем здесь неко­торые результаты, устанавливающие такого рода соответствие.

Утверждение 1: для функционалов типа Q₁ (3.11). Будем, предполагать используемую метрику евклидовой. Обозначим через Е = (E_l ..., E_k) группу из k p-мерных векторов Е_j (j = 1, 2.... k), а через S(E)= (S₁(E),…S_k(E)) – так называемое минимальное дистанционное разбиение, порождаемое точками Е = (E_l ..., E_k). А именно,

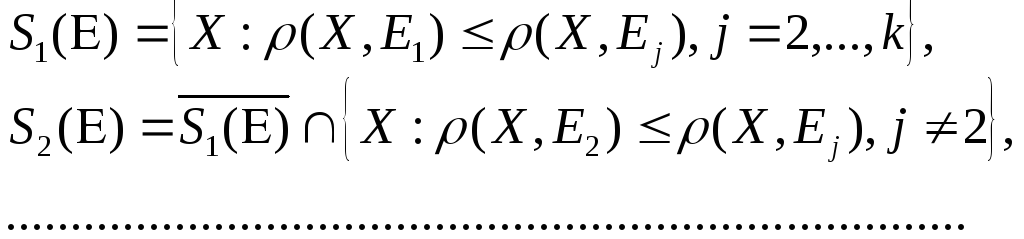
¹

Таким образом, класс S_j(Е) состоит из тех точек пространства X, которые ближе Е_j, чем ко всем остальным Е_i (i<>j). Если для некоторых точек из ­X самыми близкими являются сразу несколько век­торов E_j(j=1,…,k), то мы относим эти точки к классу с минимальным индексом.

Разбиение S=(S₁,...,S_k) называется несмещенным разбиением, если это разбиение с точностью до множеств меры нуль совпадает с минимальным дистанционным разбиением, порождаемым векторами средних

.

В работе [33] показано, что минимальное значение функционала достигается только на несмещенных разбиениях. Это означает, что оптимальное разбиение обязательно должно быть несмещенным.

Утверждение 2: для функционалов от разбиений на два класса. Следующее утверждение относится к довольно широкому классу функционалов качества разбиения совокупности на два класса. Разбиение на два класса может быть задано с помощью так называе­мой разделяющей функции. А именно, точки пространства X, на кото­рых разделяющая функция принимает неотрицательное значение, относятся к одному классу, а остальные — к другому. Поэтому поиск класса оптимальных разбиений в этом случае эквивалентен поиску класса оптимальных разделяющих функций.

Для иллюстрации дальнейшего изложения будем рассматривать вероятностную модификацию функционала Q₂’ (3.14).

Пусть расстояние ρ(X,Y) задается с помощью соотношения (3.3) потенциальной функцией вида

,

где φ_i(X) (i = 1, ..., N) — некоторая система функции на X.

Функционал Q₂’ через потенциальную функцию К(X,Y) выража­ется следующим образом:

.

Поскольку в правой части этого равенства первый интеграл не зависит от разбиения, то минимум функционала Q₂’(S) достигается на тех разбиениях, на которых функционал

достигает максимума.

Введем в рассмотрение спрямляющее пространство Z, коор­динаты z⁽ⁱ⁾ векторов Z є Z которого определяются соотношениями

z⁽ⁱ⁾=λ_iφ_i(X) (i=1,….,N).

В спрямляющем пространстве Z вероятностной мерой Р, заданной в исходном пространстве X, индуцируется своя вероятностная мера P^(Z). Однако в целях упрощения обозначений мы будем опускать ''верхний индекс Z у этой новой меры. Что касается функционала Q₂ (S), то в спрямляющем пространстве он примет вид

.

Пусть

Здесь Z^2j=[(Z,Z)]^j— числа, Z^2j+1 =[(Z, Z)]^jZ — векторы.

В работе [7] формулируется утверждение, устанавливающее класс функций в спрямляющем пространстве Z, среди которых следует ис­кать разделяющую функцию, доставляющую экстремум функционалу качества разбиения. А именно, показано, что если функционал ка­чества Ф является дифференцируемой функцией от , а вероятностное распределение Р^(Z) сосредоточено на ограниченном множестве Z и обладает непрерывной плотностью, то если экстремум функционала Ф достигается на некоторой разделяющей функции, то этот же экстремум достигается на разделяющей функции, являю­щейся полиномом r-й степени вида:

,

где

a , означает при четном ν произведение чисел c_ν и Z^ν, а при не­четном ν — скалярное произведение векторов c_ν и Z^ν.

Для функционала Q₂’ сформулированное означает, что класс раз­деляющих функций, среди которых надо искать наилучшее в спрям­ляющем пространстве разбиение, имеет вид

,

где

(3.22)

и

,

Класс разделяющих функций в спрямляющем пространстве очевидным образом определяет класс разделяющих функций в исходном простран­стве X.

Если К (X,Y) = (X,Y) является скалярным произведением век­торов X и Y, то спрямляющее пространство Z совпадает с исходным пространством X, а метрика, задаваемая потенциальной функцией К (X, Y), совпадает с обычной евклидовой метрикой. Функционалы Q₂ и Q'₂, рассматриваемые относительно этой метрики, совпадают с точностью до константы.

В этом случае, как нетрудно видеть, разбиение, задаваемое разде­ляющей функцией f (Z), является несмещенным разбиением.

д) Функционалы качества разбиения как результат применения метода максимального правдоподобия, к задаче статистического оцени­вания неизвестных параметров. Приведем здесь пример, иллюстри­рующий возможность обоснования выбора общего вида функционала качества разбиения на классы в ситуациях, в которых исследователю удастся «втиснуть» свою задачу в рамки одной из классических моде­лей.

Пусть априорные сведения позволяют определить i-й однород­ный класс (кластер) как нормальную генеральную совокупность на­блюдений с вектором средних a_i ковариационной матрицей Σ_i. При этом a_i и Σ_i вообще говоря, неизвестны. Нам известно лишь, что каждое из наблюдений Х_1, Х₂, ..., Х_n извлекается из одной из k нор­мальных генеральных совокупностей N (a_i,Σ_i), i= 1, 2, ..., k. Задача исследователя — определить, какие из n_i исходных наблюдений из­влечены из класса N (a₁,Σ₁), какие n₂ наблюдений извлечены из клас­са N (a₁,Σ₁), и т. д. Очевидно, числа n₁,n₂, ..., n_k, вообще говоря, также неизвестны.

Если ввести в рассмотрение вспомогательный векторный параметр γ=(γ₁,γ₂,….,γ_n), в котором компонента γ_i определяет помер класса, к которому относится наблюдение Х_i, т. е. γ_i=l, если X_i є N(a_l,Σ_l), i = 1, 2, ..., п, то задачу разбиения на классы можно формулиро­вать как задачу оценивания неизвестных параметров γ₁,γ₂,….,γ_n при «мешающих» неизвестных параметрах a_i и Σ_i , i = 1,2, ..., k. Обозначив весь набор неизвестных параметров с помощью θ, т. е. θ = (γ,a₁,…,a_k,Σ₁,….,Σ_k) и пользуясь известной [4] техникой, получаем логарифмическую функцию правдоподобия для наших наблюдений Х_1, Х₂, ..., Х_n.

. (3.23)

Как известно, оценка параметраи по методу максимальногоправдоподобия находится из условия .

Поэтому естественно было бы попытаться найти такое разбиение на классы S₁,S₂, ..., S_k, а также такие вектора средних a_i и кова­риационные матрицы , при которых величина —2l(θ) достигала бы своего абсолютного минимума¹.

При известном разбиении γ оценками максимального правдо­подобия для a_l будут «центры тяжести» классов

Подставляя их в (3.23) вместо a_l и воспользовавшись очевидными тождественными преобразованиями, приходим к эквивалентности задачи поиска минимума функции — 2l(θ), определенной соотноше­нием (3.23), и задачи поиска минимума выражения

(3.24)

или, что то же, выражения

(3.25)

В последнем выражении W_l выборочная ковариационная матрица, вычисленная по наблюдениям, входящим в состав l-го класса (3.13).

Анализ выражений (3.24) и (3.25) в некоторых частных случаях немедленно приводит к следующим интересным выводам:

— если ковариационные матрицы исследуемых генеральных сово­купностей равны между собой и известны, то задача оценивания не­известного параметра θ по методу максимального правдоподобия равносильна задаче разбиения наблюдений X_i на классы, подчинен­ной функционалу качества разбиения вида Q₁(S), в котором под рас­стоянием ρ подразумевается расстояние Махаланобиса;

—- если ковариационные матрицы исследуемых генеральных сово­купностей равны между собой, но не известны, то, подставляя в (3.25) вместо Σ_l = Σ ее оценку максимального правдоподобия

убеждаемся в эквивалентности задачи оценивания (по методу мак­симального правдоподобия) параметра θ и задачи поиска разбиения наблюдений X_i на классы, наилучшего в смысле функционала ка­чества Q₃(S);

— если ковариационные матрицы исследуемых генеральных со­вокупностей не равны между собой и не известны, то, подставляя в (3.25) вместо Σ_l их оценки максимального правдоподобия W_l убеждаемся в эквивалентности задачи оценивания по методу макси­мального правдоподобия параметра θ и задачи поиска разбиения наблюдений X_i на классы, наилучшего в смысле функционала ка­чества Q₄ (S).

В [68] авторы пытаются конструировать алгоритмы, реализующие идею получения оценок максимального правдоподобия для параметра θ. Однако нам представляется главная ценность подобного подхода лишь в его методологической, качественной стороне, в том, что он по­зволяет строго осмыслить и формализовать некоторые функционалы качества разбиения, введенные ранее чисто эвристически. Конструк­тивная же сторона подобного подхода упирается в трудно преодолимые препятствия вычислительного плана, связанные с колоссальным ко­личеством переборов вариантов уже при сравнительно небольших размерностях р и объемах выборки.