4.9. Область решений линейной разделяющей функции

Рассмотрим снова случай двух классов. Пусть даны обучающие наблюдения . Мы хотим построить решающее правило распознавания, ограничившись параметрическим семейством решающих правил видана основе построения линейной разделяющей функции вида. Предположим, что существует такая разделяющая функция, что вероятность неправильной классификации хотя бы одного наблюдения из обучающей выборки с ее помощью чрезвычайно мала. Если такую разделяющую функцию удается построить, то обучающую совокупность будем считать линейно разделимой. Естественно предположить, что в общем случае существует некоторое множество гиперплоскостей, разделяющих данную обучающую последовательность на два класса. Поэтому в общем случае существует вполне определенное множество направляющих векторов таких гиперплоскостей, образующих область решений в расширенном пространстве (рис. 4.4).

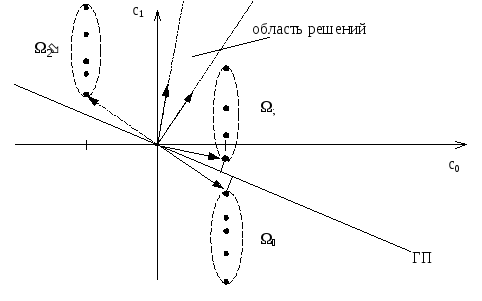
Рис. 4.4. Область решений для двух классов.

Очевидно, что множество направляющих векторов всех гиперплоскостей, разделяющих два класса, образуют конус в расширенном пространстве. Границами конуса являются направляющие векторы таких гиперплоскостей, которые сами проходят через некоторые граничные точки множеств _и_. Для направляющих векторовcиз области решений все объекты обучающей совокупности классифицируются правильно, то есть выполнено:

где крайние положения при варьировании направляющего вектора определены моментом, когда в первый раз выполнились условия ,и,для некоторых граничных точек из_и_.

Часто знак координат объектов из класса _инвертируют. Тогда все объекты обучающей совокупностиклассифицируются правильно, если, а крайние положения при варьировании направляющего вектора определяются выполнением условиядля некоторых граничных точек из.

Напомним некоторые определения. Пусть в n- мерном пространстве заданы два вектораx₁ иx₂. Тогда вектор разностинаправлен из точкиx₁ в точкуx₂, а векторприлежит на отрезке, соединяющем точкиx₁ иx₂. Векторxназывается выпуклой линейной комбинацией точекx₁ иx₂и при варьированиипробегает все точки отрезка между точкамиx₁ иx₂.

Множество точек называется выпуклым, если любые две его точки можно соединить отрезком, любая точка которого также принадлежит этому множеству.

Граничной точкой множества называется точка, в окрестности которой при любомсодержатся точки, не принадлежащие данному множеству. В противном случае такая точка является внутренней точкой множества. Здесьокрестностью некоторой точкиaназывается множество точекx, удовлетворяющих условию.

Множество называется замкнутым, если оно содержит все свои граничные точки.

Выпуклой оболочкой замкнутого выпуклого множества называется множество его граничных точек. Выпуклой оболочкой невыпуклого замкнутого множества называется множество граничных точек минимального выпуклого замкнутого множества, охватывающего данное.

Гиперплоскость называется опорной, если она проходит через некоторую граничную точку выпуклого замкнутого множества или, другими словами, касается его выпуклой оболочки.

Можно доказать, что, если выпуклые оболочки двух множеств не пересекаются и не соприкасаются, то их можно разделить более, чем одной гиперплоскостью, проходящей в расширенном пространстве через начало координат, множество направляющих векторов которых образуют выпуклый конус. Границы выпуклого конуса определяются направляющими векторами опорных гиперплоскостей, проходящих через начало координат.

Тогда в качестве разделяющей можно взять любую из гиперплоскостей, направляющий вектор которой лежит в области решений.

Но, как правило, из всего множества направляющих векторов в области решений стремятся выбрать один или хотя бы некоторое подмножество, являющихся в некотором смысле оптимальными по отношению ко всем векторам области решений.

Представление об оптимальности разделяющей гиперплоскости основано на том, что для разных разделяющих гиперплоскостей с направляющими векторами из области решений существуют в общем случае различные вероятности неправильной классификации. Поэтому оптимальная в некотором смысле гиперплоскость должна, в итоге, обеспечить уменьшение вероятности неправильной классификации.

Предположение о линейной разделимости обучающей совокупности на два класса _и_при ее неизвестных вероятностных характеристиках позволяет сформулировать понятие оптимальности разделяющей гиперплоскости непосредственно в терминах гиперплоскостей, косвенно обеспечивая уменьшение вероятности ошибочной классификации.

Рассмотрим исходное (нерасширенное) пространство. Будем считать оптимальной гиперплоскость, которая наиболее удалена от выпуклых оболочек разделяемых множеств (рис. 4. 5).

Рис. 4.5. Гиперплоскость, наиболее удаленная от выпуклых

оболочек разделяемых множеств.

Пусть и - ближайшие точки выпуклых оболочек разделяемых множеств, где- минимальное расстояние среди всех точек выпуклых оболочек множеств. Тогда оптимальная гиперплоскость определяется направляющим вектороми смещением, проходя через середину отрезка, соединяющего и перпендикулярно ему.

В другом случае (рис. 4.6) в расширенном пространстве оптимальные гиперплоскости не касаются выпуклых оболочек, а их направляющие векторы находятся внутри суженной области решений , гдеb - некоторый допуск,или

.

Рис. 4.6. Суженная область принятия решений.

С другой стороны, знание вероятностных характеристик обучающей совокупности позволяет получить оптимальное решающее правило в виде байесовского классификатора. Задавшись видом параметрического семейства распределений, мы сможем определить параметры оптимальной разделяющей границы. Такую границу, как правило, можно определить как гиперплоскость в соответствующем спрямляющем пространстве.

Пусть, например, задано параметрическое нормальное семейство распределений. Пусть решающее правило

строится на основе разделяющей функции вида

, где

.

Тогда получим

Рассмотрим случай, когда , гдеE - единичная матрица. Такой случай возникает, когда признакистатистически независимы и имеют одинаковую дисперсию. Напомним, что к такому случаю можно прийти, в частности, перейдя от стандартизованной матрицы данныхXк стандартизованной матрицеYпосредством ортогонального преобразования, гдеA- матрица собственных векторов корреляционной матрицы, а- диагональная матрица с собственными числами на главной диагонали. В этом случаеи, а классыявляются гиперсферами с центрами в точках. Тогда,.

После преобразования и сокращения подобных получим разделяющую функцию

.

Если и, то, опустив 1/2, получим разделяющую функцию.

Решающее правило запишется как

.

Такое байесовское решающее правило часто называется классификатором по минимуму расстояния до эталона класса, где эталонами являются средние по классам . С другой стороны

.

Данное уравнение определяет в исходном пространстве гиперплоскость с направляющим вектором и смещением

.

Положив ии введя обозначенияи, получим уравнение оптимальной гиперплоскости, наиболее удаленной от гиперсферических оболочек классовс радиусами гиперсфер. Такая гиперплоскость проходит через середину отрезкаперпендикулярно ему. Пригиперплоскость смещается в соответствующую сторону на величину.

Рассмотрим другой случай, когда ковариационные матрицы классов совпадают , а классы являются гиперэллипсоидами с центрами в точкахи полуосями, направленными вдоль собственных векторов ковариационной матрицы. Тогда дискриминантная функция имеет вид

.

В случае байесовское решающее правило на основе такой дискриминантной функции называется классификатором по минимуму квадратичного махаланобисова расстояния до каждого из эталонов. Преобразуем выражение и получим

.

Это уравнение гиперплоскости с направляющим вектором

и смещением

.

Так как направляющий вектор cв общем случае не совпадает с вектором, то разделяющая гиперплоскость в случаепроходит через серединуне ортогонально ему. Разделяющая гиперплоскость пройдет через серединуортогонально ему, если векторлежит в направлении некоторого собственного вектора матрицы^-1, так как именно в этом случае выполненогдеявляется одним из собственных чисел(рис. 4.7).

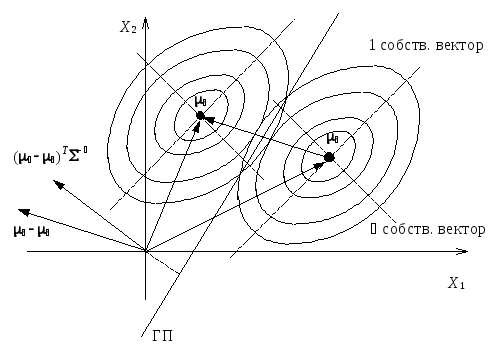
Рис. 4.7. Классификатор по минимуму махаланобисова

расстояния.