
- •92 Двоенко с.Д. Методы анализа бмд
- •4. Задачи классификации и кластер-анализа
- •4.1. Постановка задач классификации и кластер-анализа
- •4.2. Байесовское решающее правило классификации
- •4.3. Вероятности ошибок байесовского классификатора
- •4.4. Формирование решающего правила как обучение распознаванию образов
- •4.5. Восстановление плотностей распределения классов
- •4.6. Восстановление функций степени достоверности
- •4.7. Минимизация среднего риска
- •4.8. Линейные разделяющие функции
- •4.9. Область решений линейной разделяющей функции
- •4.10. Алгоритмы построения разделяющих гиперплоскостей
- •4.11. Алгоритм построения оптимальной разделяющей гиперплоскости
- •4.12. Алгоритмы кластер-анализа
4.8. Линейные разделяющие функции
Как было показано, некоторое решающее
правило
![]() ,
независимо от способа его получения,
определяет разбиение признакового
пространства на области принятия решений
,
независимо от способа его получения,
определяет разбиение признакового
пространства на области принятия решений![]() .
Полагая, что решающее правило адекватно
структуре обрабатываемых данных, мы
считаем, что данные области принятия
решений порождают разбиение всего
множества исследуемых объектовXна классы
.
Полагая, что решающее правило адекватно
структуре обрабатываемых данных, мы
считаем, что данные области принятия
решений порождают разбиение всего
множества исследуемых объектовXна классы![]() .
Поэтому мы полагаем, что посредством
решающего правила
.
Поэтому мы полагаем, что посредством
решающего правила![]() строится отображение некоторого
множества исходных образов, определенных
на универсальном множестве,
в признаковое пространство, представленное
матрицей данныхX.
строится отображение некоторого
множества исходных образов, определенных
на универсальном множестве,
в признаковое пространство, представленное
матрицей данныхX.
С другой стороны, решающее правило
![]() порождает совокупность границ, разделяющих
области, соответствующие различным
классам. Вид границ определяется решающим
правилом, где, в частности, линейное
решающее правило определяет линейные
границы.
порождает совокупность границ, разделяющих
области, соответствующие различным
классам. Вид границ определяется решающим
правилом, где, в частности, линейное
решающее правило определяет линейные
границы.
Для случая двух классов решающее правило определяет одну границу, такую, что решающее правило принимает совпадающие значения для объектов по одну сторону границы и несовпадающие значения для объектов по обе стороны границы. В таком случае решающее правило удобно определить в виде разделяющей функции вида
 .
.
В случае линейной разделяющей функции
получим
![]() .
.
Уравнение вида
![]() определяет уравнение разделяющей
гиперплоскости в признаковом пространстве.
В двухмерном пространстве это просто
прямая линия. Обозначив
определяет уравнение разделяющей
гиперплоскости в признаковом пространстве.
В двухмерном пространстве это просто
прямая линия. Обозначив![]() ,
получим уравнение гиперплоскости в
виде
,
получим уравнение гиперплоскости в
виде![]() .
Отсюда получим
.
Отсюда получим![]() ,
гдеc0- величина порога. Тогда
,
гдеc0- величина порога. Тогда
 .
.
Возьмем две точки x1иx2,
принадлежащие разделяющей границе
классови.
Очевидно, что![]() ,
откуда
,
откуда![]() .
Следовательно, векторcортогонален
вектору разности
.
Следовательно, векторcортогонален
вектору разности![]() .
Так как вектор
.
Так как вектор![]() лежит в гиперплоскости, то векторcопределяет нормаль к ней и является ее
направляющим вектором, а коэффициент
лежит в гиперплоскости, то векторcопределяет нормаль к ней и является ее
направляющим вектором, а коэффициент![]() называется ее смещением от начала
координат (вдоль вектораc).
называется ее смещением от начала
координат (вдоль вектораc).
Рассмотрим
геометрическое представление уравнения
гиперплоскости в двухмерном пространстве
(рис. 4.2). Очевидно, что для x1иx2выполнены условия![]() и
и![]() .
Смещениеc0определяется
проекцией некоторого вектора, проведенного
из начала координат, с концом, лежащим
в гиперплоскости, на ее направляющий
вектор, например,
.
Смещениеc0определяется
проекцией некоторого вектора, проведенного
из начала координат, с концом, лежащим
в гиперплоскости, на ее направляющий
вектор, например,![]() .
В данном случае
.
В данном случае![]() .
Тогда проекция некоторого произвольного
вектораxна направляющий вектор
гиперплоскости есть величина
.
Тогда проекция некоторого произвольного
вектораxна направляющий вектор
гиперплоскости есть величина![]() .
.
Так как
![]() ,
то
,
то![]() есть разность длин проекций или, другими
словами, расстояние вектораxдо
гиперплоскости. Так как в данном случае
есть разность длин проекций или, другими
словами, расстояние вектораxдо
гиперплоскости. Так как в данном случае![]() ,
то нормальный вектор направлен в сторону
областиа расстояние до гиперплоскости в данной
области положительно. В областирасстояние
до гиперплоскости считается отрицательным.
,
то нормальный вектор направлен в сторону
областиа расстояние до гиперплоскости в данной
области положительно. В областирасстояние
до гиперплоскости считается отрицательным.
Следовательно, знак линейной разделяющей
функции
![]() определяет принадлежность объектаxк одному из классовили,
а значение определяет расстояние до
гиперплоскости при условии, что ее
направляющий векторcимеет единичную
длину. Если
определяет принадлежность объектаxк одному из классовили,
а значение определяет расстояние до
гиперплоскости при условии, что ее
направляющий векторcимеет единичную
длину. Если![]() ,
то расстояние гиперплоскости до начала
координат определяется величиной
,
то расстояние гиперплоскости до начала
координат определяется величиной![]() ,
а расстояние от некоторого вектораxдо гиперплоскости определяется как
величина
,
а расстояние от некоторого вектораxдо гиперплоскости определяется как
величина![]() .
.
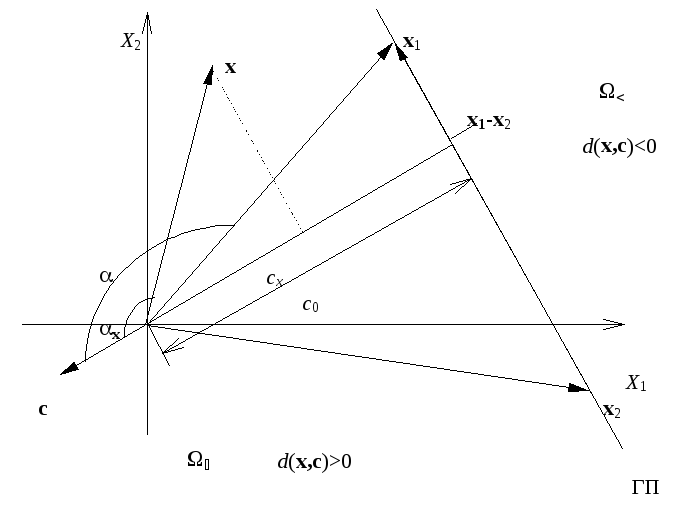
Рис. 4.2. Гиперлоскость и ее направляющий вектор.
Для случая, когда число классов
![]() удобно использовать
удобно использовать![]() различных решающих функций вида
различных решающих функций вида![]() ,
где
,
где![]() .
Например, для трех классов нужно
построить три гиперплоскости (рис. 4.3).
Как видно, в данном случае имеется
область неопределенного решения (ОНР),
когда нельзя принять решение о классе
объекта. Для такого объекта классификация
не определена.
.
Например, для трех классов нужно
построить три гиперплоскости (рис. 4.3).
Как видно, в данном случае имеется
область неопределенного решения (ОНР),
когда нельзя принять решение о классе
объекта. Для такого объекта классификация
не определена.
Рассмотрим расширенный вектор
![]() и вектор коэффициентов
и вектор коэффициентов![]() .
Тогда разделяющая функция имеет вид
.
Тогда разделяющая функция имеет вид![]() ,
а уравнение разделяющей гиперплоскости
в новом, “расширенном” пространстве
размерности
,
а уравнение разделяющей гиперплоскости
в новом, “расширенном” пространстве
размерности![]() имеет вид
имеет вид![]() .
Согласно рассмотренному выше
геометрическому представлению, всякая
гиперплоскость
.
Согласно рассмотренному выше
геометрическому представлению, всякая
гиперплоскость![]() имеет нулевое смещение, то есть проходит
через начало координат в расширенном
пространстве.
имеет нулевое смещение, то есть проходит
через начало координат в расширенном
пространстве.
В расширенном пространстве удается, в частности, избежать появления областей неопределенности решений о классе объекта (рис. 4.3). Например, в данном случае для трех классов ОНР отсутствует в расширенном пространстве, которое полностью разбито на три области, каждая из которых содержит один класс.


Рис.4.3. а) Область неопределенного решения, б) ОНР нет
