
- •Кинематика
- •1. Кинематика поступательного движения
- •2. Кинематика вращательного движения
- •Связь между величинами, характеризующими поступательное и вращательное движение
- •Динамика задачи
- •Колебания и волны
- •1. Механические колебания
- •1.1. Свободные незатухающие колебания
- •1.2. Свободные затухающие колебания
- •1.3. Вынужденные колебания
- •Упругие волны.
Кинематика
Предмет изучения механики – механическое движение, т.е. изменение с течением времени взаимного расположения тел или их частей в пространстве.
Движение происходит в пространстве и во времени.
Существует два вида движения:
поступательное (любая прямая, жестко скрепленная с телом, при движении перемещается параллельно самой себе);
вращательное (любая прямая, жестко скрепленная с телом, при движении поворачивается на некоторый угол).
Для описания движения необходимо ввести систему отсчета, представляющую собой систему координат и систему отсчета времени.
Кинематика – раздел механики, изучающий способы описания механического движения независимо от вызывающих его причин.
1. Кинематика поступательного движения
Т
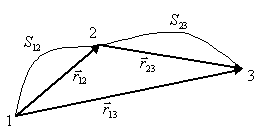 раектория
– линия, которую описывает тело или
материальная точка, при своем движении
в пространстве. По виду траектории
движение бывает прямолинейным или
криволинейным. Частным случаем
криволинейного движения есть движение
по окружности.
раектория
– линия, которую описывает тело или
материальная точка, при своем движении
в пространстве. По виду траектории
движение бывает прямолинейным или
криволинейным. Частным случаем
криволинейного движения есть движение
по окружности.
Путь
![]() –
расстояние, отсчитанное вдоль траектории.
Путь измеряется в метрах, выражается
положительным числом и складывается
арифметически.
–
расстояние, отсчитанное вдоль траектории.
Путь измеряется в метрах, выражается
положительным числом и складывается
арифметически.
![]() =
м.
=
м.
![]() .
.
Перемещение
![]() – вектор, начало которого находится в
начальной точке, а конец – в конечной
точке движения. Как любой вектор,
перемещение характеризуется численным
значением (модулем) и направлением,
складываются перемещения по правилам
сложения векторов, т.е. геометрически.
– вектор, начало которого находится в
начальной точке, а конец – в конечной
точке движения. Как любой вектор,
перемещение характеризуется численным
значением (модулем) и направлением,
складываются перемещения по правилам
сложения векторов, т.е. геометрически.
![]() =
м.
=
м.
![]() .
.
Если материальная
точка за равные, сколь угодно малые
промежутки времени
![]() ,
проходит равные участки пути
,
проходит равные участки пути
![]() ,
то движение называют равномерным.
,
то движение называют равномерным.
Скорость
в этом случае
![]() .
.
В случае неравномерного
движения в рассмотрение вводится средняя
скорость
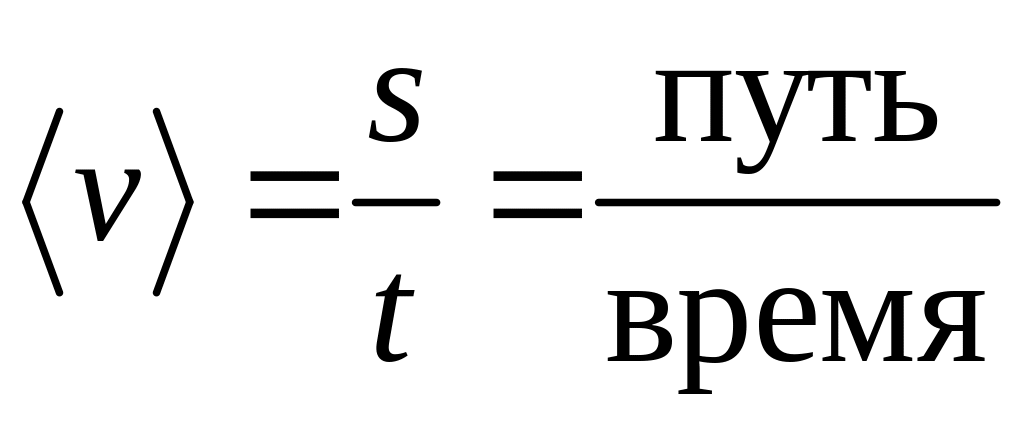 .
.
Скорость в данный момент времени (мгновенная скорость):
![]()
![]()
Поскольку при описании движения необходимо учитывать не только численное значение скорости, но и ее направление, то под скоростью понимают векторную величину
![]() .
.
![]()
Для модуля скорости:
 .
.
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() - составляющие скорости, а
- составляющие скорости, а
![]() ,
,
![]() ,
,
![]() -
орты декартовой системы координат.
-
орты декартовой системы координат.
Ускорение – векторная величина, характеризующая изменение скорости во времени..
![]() .
.
![]() .
.
Учитывая, что
![]() ,
рассмотрим три вида движения.
,
рассмотрим три вида движения.
1.
![]() (движение прямолинейное
неравномерное)
(движение прямолинейное
неравномерное)
![]() .
.
Тангенциальное
ускорение
![]() характеризует изменение скорости по
модулю.
характеризует изменение скорости по
модулю.
2.
![]() (движение криволинейное
равномерное)
(движение криволинейное
равномерное)
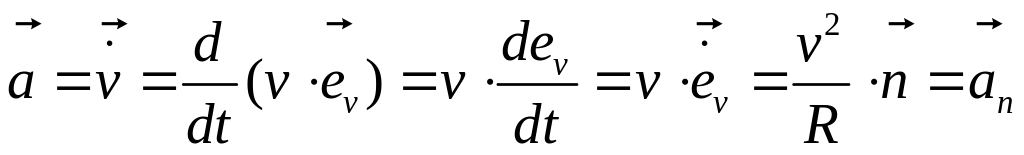
Нормальное ускорение характеризует изменение скорости по направлению.
3.
![]() (движение неравномерное
криволинейное)
(движение неравномерное
криволинейное)
![]()
 .
.
![]() .
.
Равноускоренное движение описывается формулами:
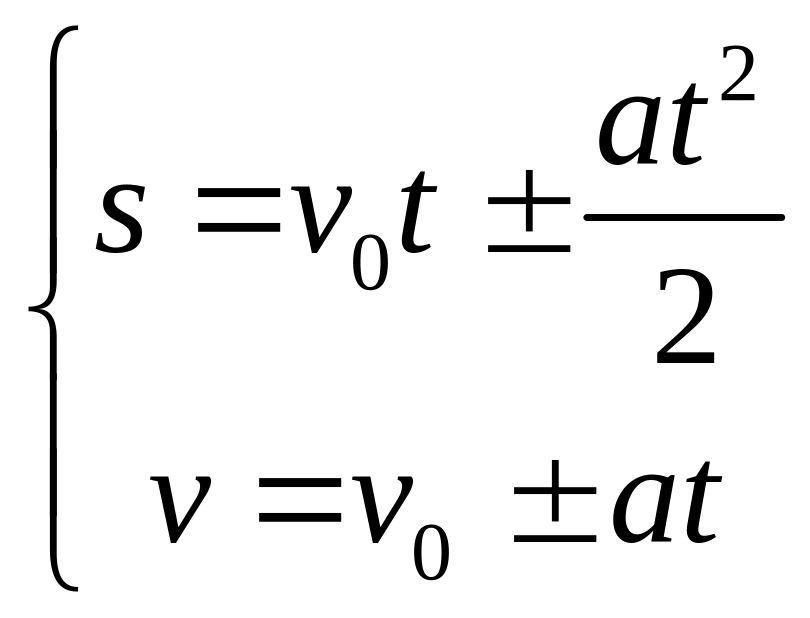 .
.
2. Кинематика вращательного движения
Д
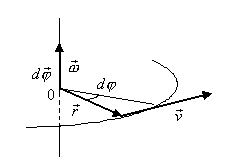 ля
равномерного прямолинейного движения
скорость характеризует быстроту
изменения перемещения. Для вращательного
движения угловая скорость определяет
быстроту изменения углового
перемещения
ля
равномерного прямолинейного движения
скорость характеризует быстроту
изменения перемещения. Для вращательного
движения угловая скорость определяет
быстроту изменения углового
перемещения
![]() .
Угловое перемещение
есть векторная величина, модуль которой
равен углу поворота, направленный вдоль
оси вращения так, чтобы из его конца
поворот тела был виден происходящим
против часовой стрелки.
.
Угловое перемещение
есть векторная величина, модуль которой
равен углу поворота, направленный вдоль
оси вращения так, чтобы из его конца
поворот тела был виден происходящим
против часовой стрелки.
Тогда угловая
скорость
![]()
![]() ,
,
![]() .
.
Направление вектора
![]() и
и
![]() совпадают. Кроме того, направление
выбирается так, чтобы, если смотреть с
вершины
,
то движение должно казаться происходящим
против часовой стрелки, т.е. векторы
линейной скорости
совпадают. Кроме того, направление
выбирается так, чтобы, если смотреть с
вершины
,
то движение должно казаться происходящим
против часовой стрелки, т.е. векторы
линейной скорости
![]() ,
угловой скорости
и радиус вектор точки
должны образовывать правовинтовую
систему.
,
угловой скорости
и радиус вектор точки
должны образовывать правовинтовую
систему.
Изменение угловой
скорости характеризуется угловым
ускорением
![]() .
.
![]() ,
,
![]() .
.
Для ускоренного движения направления векторов угловой скорости и углового ускорения совпадают, а для замедленного – противоположны.
Следует отметить, что векторы , и являются псевдовекторами, т.к. их направления выбираются условно.
