§ 2. Дифракция Фраунгофера на щелях

Р

Рис. 4 Дифракция Фраунгофера на одной щели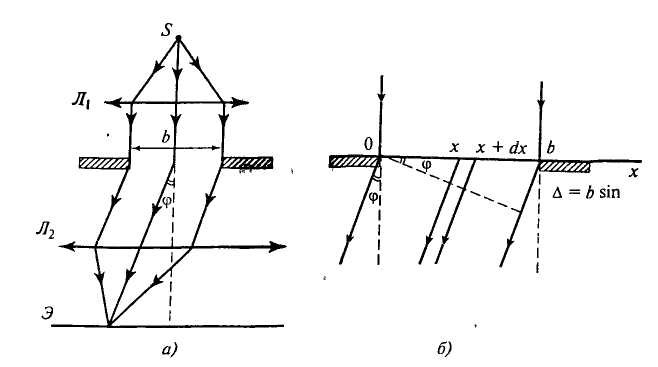

ассмотрим вначале дифракцию в параллельных лучах (дифракцию Фраунгофера) на одной щели. Пусть на щель шириной b падает нормально пучок параллельных лучей света. Вторичные волны за щелью распространяются в принципе во всех направлениях. Однако интенсивность этих вторичных волн в разных направлениях может быть различной. Выясним, какова будет интенсивность света, распространяющегося за щелью в некотором произвольном направлении под углом  к направлению падающего света (рис.4).

Оптическая разность хода между крайними лучами, проходящими через щель и распространяющимися под углом , будет равна  = bsin (см. рис.4б). Тогда число открытых зон Френеля, которые помещаются в щели, можно рассчитать по формуле

(15)

Зоны Френеля в рассматриваемой задаче представляют собой одинаковые плоские полоски, лежащие в плоскости щели и параллельные этой щели. В частном случае, когда , сама щель является зоной Френеля. Если в щели помещается четное число зон Френеля, то в этом случае должен наблюдаться минимум диффракционной картины. Отличительной особенностью дифракции Фраунгофера, которая связана с тем, что площади зон Френеля в этом случае строго совпадают и лучи распространяются под одинаковым углом, является равенство нулю интенсивности света в минимуме. Итак, минимум дифракционной картины на одной щели реализуется при условии

, m = 1, 2, 3, ... (16)

Соответственно максимум дифракционной картины наблюдается, когда открыто нечетное число зон Френеля, то есть при условии

, m = 1, 2, 3, ... (17)

Кроме того, максимум дифракционной картины должен наблюдаться в направлении  = 0, поскольку в этом направлении все вторичные волны, идущие от щели, имеют одинаковую фазу и усиливают друг друга. В отличие от других максимумов, положение которых на экране Э зависит от длины волны падающего света, положение центрального максимума (при  = 0) является общим для любых длин волн.

§ 3. Дифракционные решетки

С

Рис.5 Дифракционная решетка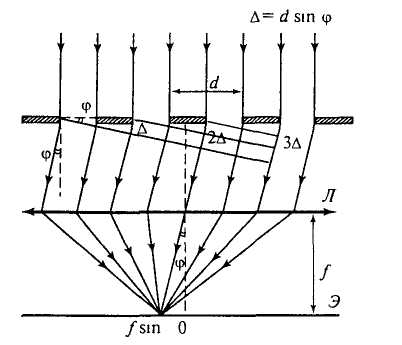

овокупность из N правильно (на одинаковом расстоянии) расположенных, одинаковых и параллельных щелей называется одномерной дифракционной решеткой. Одномерной потому, что оптическая неоднородность (прозрачность в нашем случае) является функцией одной координаты х.

Е

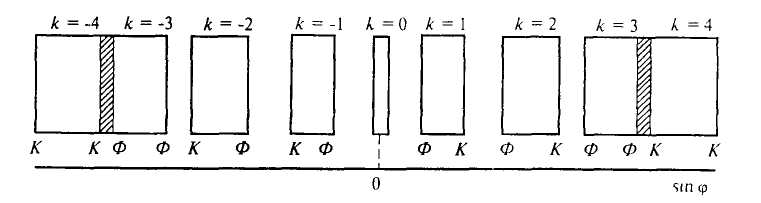
Рис. 6. Спектр дифракционной решетки

сли на дифракционную решетку падает белый свет, то все максимумы, кроме центрального ( = 0), разложатся в спектры. Причем фиолетовый край спектра (т.е. самый коротковолновый из видимого диапазона) будет смещен относительно центрального максимума меньше всего, а красный край спектра – больше всего. На рис.6 схематично изображены спектры дифракционной картины, возникающие на дифракционной решетке при падении на нее белого света. В центре находится узкий максимум нулевого порядка (этот максимум имеет белый цвет, поскольку свет в этом направлении по длинам волн, то есть по цветам, не расщепляется). По обе стороны симметрично центральному нулевому максимуму расположены два спектра первого порядка (k = 1), затем два спектра второго порядка (k = 2) и т

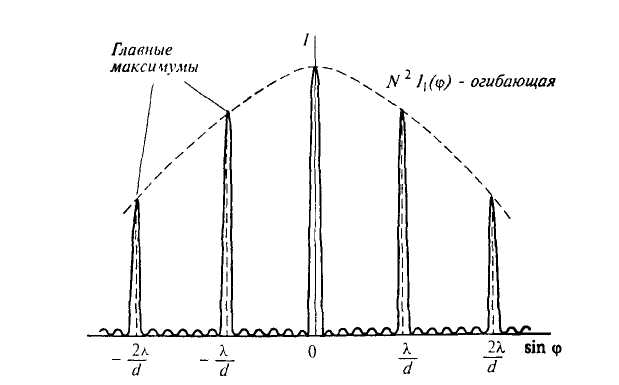
Рис 7 Дифракционная картина для N щелей

.д. По мере увеличения порядка дифракционного спектра его ширина возрастает, а интенсивность уменьшается. Кроме того, для высоких порядков дифракционных спектров характерно наложение красного участка спектра порядка k и фиолетового участка спектра порядка k+1.

Будем считать, что ширина каждой щели равна b, а расстояние между соответствующими точками щелей равно d (рис.5). Условие

bsin = m , m = 1, 2, ... (18)

определяет направления, в которых каждая щель имеет минимум интенсивности, то есть не светит (т.к. минимум абсолютный). Поэтому условие (18) называют условием дифракционных минимумов.

При выполнении условия

dsin = k , k = 0, 1, 2, ... (19)

лучи от щелей приходят на экран в одинаковой фазе, то есть усиливают друг друга. Поэтому условие (19) называется условием главных дифракционных максимумов.

Если реализуется условие

, k = 0, 1, 2, ... (20)

то лучи от щелей приходят в точку наблюдения в противофазе и полностью гасят друг друга. Условие (20) называется условием дополнительных дифракционных минимумов, где i = 1, 2, ... , (N–1) – номер дополнительного минимума между двумя соседними главными максимумами. Таким образом, число дополнительных минимумов между соседними главными максимумами на единицу меньше числа щелей. Если число щелей достаточно велико, то дифракционная картина представляет собой узкие линии, соответствующие главным максимумам, между которыми интенсивность результирующей волны практически равна нулю.

Дифракционная решетка позволяет разлагать падающий свет на составляющие (по длине волны), то есть является спектральным прибором. Любой спектральный прибор (в том числе и дифракционная решетка) характеризуется дисперсией и разрешающей способностью.

Угловой дисперсией спектрального прибора называется величина , где d – угловое расстояние между спектральными линиями, отличающимися по длине волны на d. Чтобы найти угловую дисперсию дифракционной решетки, продифференцируем условие главного максимума по . В результате этого дифференцирования получим

(21)

При небольших углах (  0, cos  1) угловая дисперсия дифракционной решетки оказывается тем выше, чем больше порядок спектра k и чем меньше период решетки d. Формула (21) объясняет экспериментально наблюдаемое увеличение ширины спектра с ростом k.

Линейная дисперсия спектрального прибора определяется как отношение линейного расстояния dl между двумя спектральными линиями с длинами волн  и +d к величине этого интервала d. Поскольку линейное положение дифракционной линии на экране (т.е. в фокальной плоскости) связано с углом соотношением l = ftg то имеем

(22)

При небольших углах (  0, cos  1) линейная дисперсия связана с угловой дисперсией простым соотношением D* = fD, где f – фокусное расстояние линзы, которая используется для формирования дифракционной картины на экране.

Возможность раздельно воспринимать две близко расположенные спектральные линии характеризуется разрешающей способностью, которая определяется как

, (23)

где – минимальная разность длин волн двух спектральных линий, еще воспринимаемых раздельно.

Согласно критерию Рэлея

две спектральные линии разрешаются (воспринимаются раздельно), если главный максимум одной волны дифракционного спектра расположен не ближе, чем первый дополнительный минимум другой волны.

Математически этот критерий может быть записан в виде

, (24)

откуда получаем (т.к. )

R = kN (25)

Таким образом, разрешающая способность дифракционной решетки будет тем выше, чем больше порядок спектра и чем больше число щелей у решетки.

По устройству дифракционные решетки подразделяются на пропускающие и отражательные. Пропускающие решетки изготавливаются из стеклянных или кварцевых пластин путем нанесения алмазным резцом ряда параллельных штрихов. Промежутки между штрихами являются щелями. Отражательные решетки изготавливаются нанесением алмазным резцом штрихов на поверхности металлического зеркала. Лучшие решетки содержат более тысячи штрихов на 1 мм решетки (т.е. d  10^-6 м).

Распределение энергии световой волны по спектральным линиям дифракционной решетки таково, что значительная часть этой энергии сосредоточена в спектре нулевого порядка (непригодного для исследования спектрального состава падающего света). По мере перехода к высшим порядкам энергия световой волны быстро убывает. Поэтому о спектральных приборах на основе обыкновенной дифракционной решетки говорят, как о мало светосильных.

Важным усовершенствованием дифракционных решеток, предложенным Рэлеем и осуществленным на практике Вудом, явилось введение дополнительной разности хода в пределах каждого штриха решетки. Это достигается специальной гравировкой решетки, в результате чего лучи, идущие в направлении нулевого (центрального) максимума начинают гасить друг друга, а доля световой энергии, идущая в направлении других максимумов спектра, возрастает. Такие решетки могут работать как на просвет, так и на отражение и обладают значительно более высокой светосилой. Следует подчеркнуть, что в таких решетках регулярным образом изменяется не амплитуда падающей волны (что достигается в обычной решетке за счет изменения ее прозрачности), а фаза волны. Поэтому такие решетки называются фазовыми. Современные фазовые решетки, так называемые эшеллеты (имеющие практически треугольный профиль штриха), позволяют концентрировать до 7080% падающего на решетку света в спектр какого-либо одного ненулевого порядка. Широкое применение на практике нашли пластмассовые копии с гравированных решеток – реплики.