Дифракция света

Дифракцией света называют совокупность явлений, которые обусловлены волновой природой света и наблюдаются при его распространении в среде с резко выраженными оптическими неоднородностями (например, при прохождении через отверстие в непрозрачном экране, вблизи границ непрозрачных тел и т.д.).

В более узком и наиболее употребительном смысле под дифракцией света понимается огибание лучами света контура непрозрачных тел и, следовательно, проникновение света в область геометрической тени.

Различают два вида дифракции. Если источник света и точки наблюдения дифракции находятся на конечных расстояниях от препятствия, вызывающего эту дифракцию, в результате чего нельзя пренебречь кривизной волновой поверхности в области оптической неоднородности, то говорят о дифракции Френеля. В том случае, когда источник света и точка наблюдения находятся настолько далеко от препятствия, вызывающего дифракцию, что волновая поверхность в области оптической неоднородности представляет собой плоскость, то говорят о дифракции Фраунгофера. Последнюю удобно наблюдать, если источник света и точки наблюдения поместить в фокальные плоскости соответствующих линз. Понятно, что принципиальной разницы в физике процессов, происходящих при дифракции Фраунгофера и Френеля, нет.

Всякая дифракционная задача, если ее рассматривать строго, сводится к нахождению решения уравнений Максвелла, однако на практике обычно применяют нестрогие методы решения дифракционных задач, основанные на так называемом принципе Гюйгенса – Френеля.

§ 1. Принцип Гюйгенса – Френеля. Дифракция Френеля на простейших преградах

Еще в 1678 году голландский ученый Х.Гюйгенс (1629 – 1695) для объяснения закономерностей распространения волн использовал сформулированный им принцип (принцип Гюйгенса), согласно которому

каждый элемент волнового фронта в настоящий момент времени является центром вторичных элементарных волн, огибающая которых будет фронтальной поверхностью в следующий момент времени.

П

Рис. 3 Принцип Гюйгенса-Френеля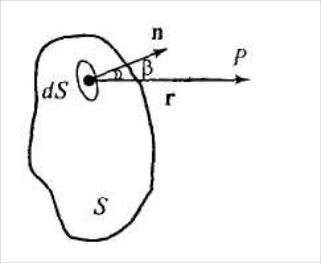

о сути дела принцип Гюйгенса есть геометрический рецепт построения волновых фронтов. Он позволяет на качественном уровне объяснить проникновение световых волн в области геометрической тени, однако не объясняет немонотонное изменение интенсивности падающего света при последовательном перемещении вдоль экрана. Для объяснения наблюдаемых закономерностей распространения света вблизи оптических неоднородностей Френель в 1815 году дополнил принцип Гюйгенса представлением об интерференции вторичных волн. Принцип Гюйгенса – Френеля можно сформулировать следующим образом:

каждый элемент волнового фронта служит источником вторичных когерентных волн; световая волна в любой точке вне этой поверхности может быть представлена как результат интерференции вторичных когерентных волн.

Согласно принципу Гюйгенса – Френеля каждый элемент dS волнового фронта S (рис.3) является источником сферической волны, амплитуда которой пропорциональна dS. Поскольку амплитуда сферической волны обратно пропорциональна расстоянию до точки наблюдения, то в т.P от элемента dS приходят колебания вектора , модуль вектора которого определяется по формуле

, (13)

где (t+₀) – фаза колебаний в месте расположения элемента поверхности dS; – волновое число,  – длина волны падающего света, r – расстояние от одного элемента до точки наблюдения P. Значение величины a₀ определяется амплитудой световой волны в точке расположения элемента dS. Коэффициент C() уменьшается с увеличением угла  между нормалью к площадке dS и направлением от dS к точке P, причем при коэффициент = 0. Согласно принципу Гюйгенса – Френеля, результирующее колебание в т.P представляет собой суперпозицию колебаний, распространяющихся от всех элементарных участков поверхности S, т.е.

(14)

В общем случае расчет результирующего колебания E по формуле (14) является достаточно сложной в математическом смысле задачей. Однако во многих практически важных случаях удается приближенно рассчитать дифракционную картину с помощью так называемого метода зон Френеля без непосредственного интегрирования выражения (14).