
- •Основы расчета конструкций по предельным состояниям
- •Нормативные и расчетные нагрузки. Нормативные и расчетные сопротивления материалов
- •Основные свойства (преимущества и недостатки) металлических и железобетонных конструкций
- •Основные положения расчет прочности центрально сжатых и центрально растянутых стальных элементов. Понятие предельной гибкости
- •Проектирование центрально сжатых стальных элементов
- •Виды сварных швов. Конструктивные требования к сварным соединениям
- •Понятия об общей устойчивости стальных балок и местной устойчивости полок стальных балок
- •Типы сечений стальных сплошных и сквозных центрально сжатых колонн
- •1. Типы сквозных колонн
- •Конструкции баз стальных колонн при различных вариантах сопряжении с фундаментом (шарнирное, жесткое)
- •Расчет прочности нормальных сечений изгибаемых малоармированных железобетонных элементов
- •Расчет прочности нормальных сечений изгибаемых переармированных железобетонных элементов
- •Расчет прочности наклонных сечений изгибаемых железобетонных элементов
- •Особенности расчета прочности внецентренносжатых железобетонных элементов (для случаев с малыми эксцентриситетами и большими эксцентриситетами)
- •Определение момента трещинообразования изгибаемых железобетонных элементов
- •Определение ширины раскрытия трещин изгибаемых железобетонных элементов
- •Особенности определения прогибов изгибаемых железобетонных элементов
- •Виды стропильных ферм
- •Типы стропильных балок
- •Виды сборных железобетонных плит
- •Принципы расчета свайных фундаментов
- •Виды свай. Типы свайных фундаментов
- •Типы конструктивного исполнения фундаментов мелкого заложения (фмз)
- •Типы каркасов многоэтажных зданий
- •1. Конструктивные схемы зданий
- •Обеспечение пространственной жесткости рамных каркасов
- •Обеспечение пространственной жесткости связевых каркасов
Понятия об общей устойчивости стальных балок и местной устойчивости полок стальных балок
Проверка общей устойчивости изгибаемых элементов
Предельное состояние изгибаемого элемента может наступить и до исчерпания прочности - при потере устойчивости плоской формы изгиба (общей потере устойчивости). Это явление аналогично продольному изгибу центрально сжатых стержней. Вначале балка изгибается в своей плоскости, совпадающей с плоскостью главной оси инерции сечений и плоскостью действия внешней нагрузки. Но с достижением балкой критических напряжений она закручивается и выходит из плоскости изгиба. В поясах балки затем появляются пластические деформации и при нагрузке, несколько превышающей критическую, балка теряет несущую способность.
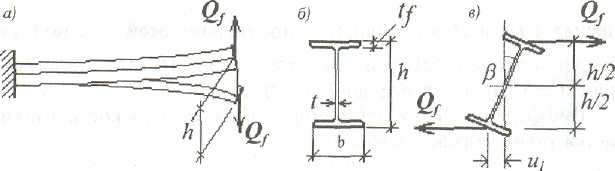
Рассмотрим это явление на примере однопролетной двутавровой балки, работающей в условиях чистого изгиба ( рис. 5.10).
Сечение на расстоянии z от опоры в начальный момент потери устойчивости поворачивается на угол а упругая ось балки повернется при этом ( в плане) на угол а .
Основные зависимости между усилиями и деформациями для рассматриваемого сечения запишем в виде
МХ1 Мх = М;
МУ1 = -М
Мz1 = Ма = Mdu/dz,
где МХ1,, МУ1, Мz1 - моменты относительно осей местной системы координат (для рассматриваемого сечения); Мх (М) --действующий в плоскости балки изгибающий момент.
Дифференциальное уравнение изгиба из плоскости балки запишется таким образом в виде
d2и/ dz2 = МУ1 / (EJy) = -М / (EJy) .
Внешний крутящий момент Mz1 , уравновешивается двумя внутренними: от касательных напряжений, вызванных свободным кручением Мt и от касательных напряжений, вызванных изгибом полок при стесненном кручении с депланацией сечений Mq (рис. 5.11).
С учетом характера эпюры изгибающих моментов и места приложения поперечной нагрузки по высоте сечения выражение для критического момента приобретает следующий вид:
где - учитывает полноту эпюры изгибающих моментов, с - место приложения нагрузки.
Практически расчет сводится к введению коэффициента снижения напряжений b = cr / m . Коэффициент b записывается в функции от = BRy/E.
Расчетная формула проверки общей устойчивости балки:
M /bW Ryc
Значения b определяют с учетом влияния возможного развития пластических деформаций при совместном действии косого изгиба и кручения в момент потери устойчивости; их принимают равными:
b = 1 При 1 0,85
b = 0,68 + 0,21 b (но не более 1) при 1 > 0,85.
![]()
Устойчивость полки изгибаемого стержня.
 На
примере полки стального
изгибаемого стержня приведем схему
аналитической оценки
условий устойчивости пластинки и
определения ее параметров,
заведомо гарантирующих местную
устойчивость полки при полном
использовании прочности стали. Примем
(в запас устойчивости) шарнирное
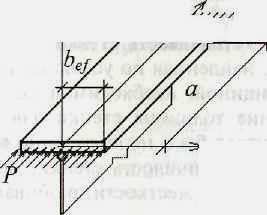
опирание полки на стенку (рис. 5.13).
Пластинка, сжатая
усилиями Р,
будет
неустойчивой, если станет возможным ее
равновесие
в искривленном состоянии.
На
примере полки стального
изгибаемого стержня приведем схему
аналитической оценки
условий устойчивости пластинки и
определения ее параметров,
заведомо гарантирующих местную
устойчивость полки при полном
использовании прочности стали. Примем
(в запас устойчивости) шарнирное
опирание полки на стенку (рис. 5.13).
Пластинка, сжатая
усилиями Р,
будет
неустойчивой, если станет возможным ее
равновесие
в искривленном состоянии.
Соотношение размеров сечения полки, при котором заведомо обеспечена местная устойчивость, может быть найдено из условия полного использования прочности материала (Ry).
На практике приходится учитывать возможные начальные несовершенства элементов (погнутости, изгиб под поперечной нагрузкой) и другие неблагоприятные факторы. Так, для не-окаймленной полки двутавра и тавра оно составляет
![]()
