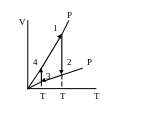Докажите, что молярная масса

![]() (1)
(1)
где
![]() – масса молекулы (атома);
– масса молекулы (атома);
![]() (
(![]() –
масса атома изотопа углерода
–
масса атома изотопа углерода
![]() С).
С).
Решение:
по определению – масса одного моля, т.е.
![]() (2)
(2)
Выражение (2) преобразуем к виду:
![]() (3)
(3)
Число Авогадро – число атомов в моле – запишем для одного моля изотопа С.
![]() .
.
Отсюда,
![]() .
(4)
.
(4)
Подставим (4) в (3) и получим соотношение (1) – что и требовалось доказать.
Сколько молекул содержится в стакане воды?
-


Составим пропорцию:

Отсюда,
 .
.Подставим численные значения (
 )
)

Вычислить массу моля электронов.
Как, зная плотность
 и молярную массу
,
найти число молекул вещества в единице
объема?
и молярную массу
,
найти число молекул вещества в единице
объема?
-

– масса единицы объема – содержит
 молекул;
молекул;– масса одного моля – содержит
 молекул.
молекул.Составим пропорцию:

Отсюда:
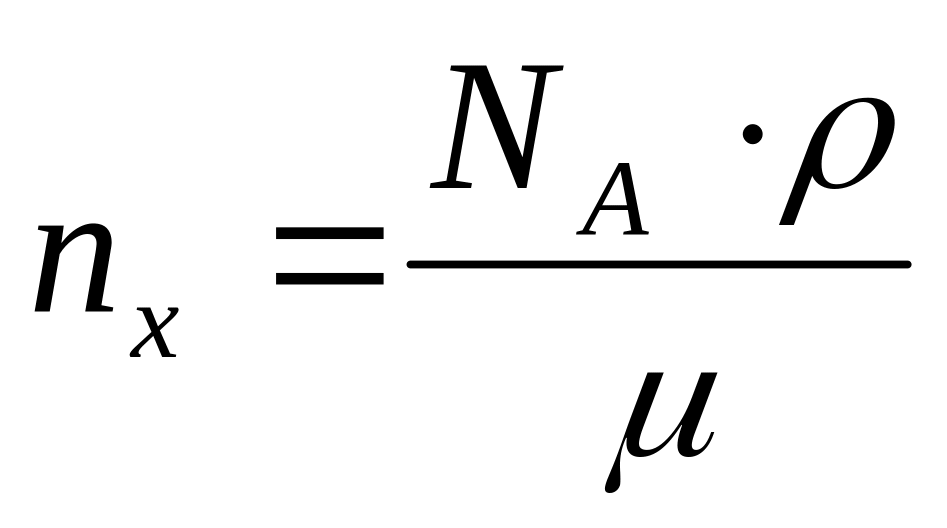 .
.
Изобразить для идеального газа графики изохорного, изобарного и изотермического процессов в осях (P,V); (T,V); (P,T). Графики изобразить проходящими через общую для них точку.
Решение:
Запишем уравнение Менделеева-Клапейрона:
![]() (1)
(1)
T = const, следовательно, PV = const (если m = const), т.е. P = const/V - гипербола.
-

1 – изотерма (T = const);
2 – изобара (P = const);
3 – изохора (V = const).
Чтобы построить график V(T) для изобарного процесса, перепишем (1) в виде:
![]()
или V = T ∙const. График – прямая линия, проходящая через 0.
-

1 – изотерма (T = const);
2 – изобара (P = const);
3 – изохора (V = const).
Чтобы построить график T(P) для изохорного процесса, перепишем (1) в виде:
![]()
или T = P ∙const. График T(P) – прямая линия, проходящая через 0.
-

1 – изотерма (T = const);
2 – изобара (P = const);
3 – изохора (V = const).
6. |
|
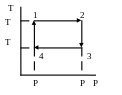
На рисунке изображен некоторый цикл в осях (P,T). Постройте этот цикл в осях (T,V).
Решение:
Процесс (1 – 2) –
изотерма при температуре T Процесс (2 – 3) – изобара при давлении P ; (4 – 1) – изобара при P < P . Сначала построим две изобары в осях (T,V):
|
|
Из
уравнения Менделеева-Клапейрона
(можно для одного моля)
|
|
Изотермы –
вертикальные отрезки. Цикл выделен
жирной линией. Обозначим состояния
(1
|
7. |
|
На рисунке в осях (P,T) изображен цикл (в виде окружности); газ – идеальный, m = const. Укажите на графике точки, в которых объем газа:
|
|
|
Решение:
Построим в осях
(P,T)
графики изохорического процесса. Из
уравнения Менделеева-Клапейрона
(для одного моля) получим:
На рис.1, следовательно, нужно провести касательные к окружности (т.е. изохоры). Точка «1» соответствует максимальному объему газа (V ); точка «2» – минимальному (V ).
|
В сосуде находится смесь: m = 7,0 г азота и m = 11 г углекислого газа при температуре T = 290 K и давлении P = 101,3 кПа (1 атм). Найти плотность этой смеси, считая газы идеальными.
-
m = 7,0 г
 = 28 г/моль
= 28 г/мольm = 11 г
 = 44 г/моль
= 44 г/мольT = 290 К
P = 101,3 кПа
Плотность газа, по определению:
 (1)
(1)где V – объем сосуда, в котором находится смесь газов.
Давление смеси складывается из парциальных давлений: азота – P и углекислого газа – P :
P = P +P
– ?
Запишем уравнение Менделеева-Клапейрона отдельно для каждого газа:
![]()
 (А)
(А)
![]() (В)
(В)
Сложим (А) и (В):
![]()
Отсюда:
 .
(2)
.
(2)
Подставим (2) в (1):
 .
.
Подставив численные значения, получим = 1,5 г/л.
Как меняется температура идеального газа, если он расширяется по закону PV
 = const?
= const?