- •Содержание
- •1. Теоретическая часть
- •1.1. Открытие углеродных нанотрубок и распространённость нанотрубок в природных и технологических средах
- •1.2. Основные типы и структура углеродных нанотрубок
- •1.3. Основные способы получения углеродных нанотрубок
- •1.4. Свойства и применение углеродных нанотрубок
- •1.4.1. Механические свойства
- •1.4.2. Баллистический транспорт в наноразмерных системах
- •1.4.3. Полупроводниковые нанотрубки
- •1.4.5. Использование асм для работы с нанотрубками
- •1.4.7. Топливные элементы на основе углеродных нанотрубок
- •1.5. Методы расчетов электронной структуры
- •1.6. Зонная структура углеродных нанотрубок
- •1.6.1. Метод сильной связи
- •1.6.2. Расчеты зонной структуры углеродных нанотрубок методом сильной связи
- •1.6.3. Другие методы расчета углеродных нанотрубок
- •1.6.4. Экспериментальные данные по зонной структуре нанотрубок
- •1.7. Метод функционала плотности
- •1.7.1. Принцип минимума функционала энергии в терминах волновых функций уравнения Шредингера
- •1.7.2. Плотность электронных состояний
- •1.7.3. Теоремы Хоэнберга – Кона
- •1.7.4. Самосогласованные уравнения Кона – Шэма и обменно-корреляционная энергия
- •1.7.5. Приближение lda
- •2. Практическая часть
- •2.1. Программное обеспечение, используемое в работе
- •2.1.1. Программный комплекс Gaussian
- •2.1.2. Базисные наборы в Gaussian
- •2.1.3. Программное обеспечение TubeGen
- •2.1.4. Файлы заданий в Gaussian
- •2.1.5. Этапы расчета
- •2.2. Задания
- •2.3. Задания для самостоятельной работы
- •2.4. Вопросы
- •2.4. Рекомендуемая форма отчётности
- •3. Рекомендуемая литература
1.6. Зонная структура углеродных нанотрубок
1.6.1. Метод сильной связи
Исследования дисперсионных свойств углеродных наноматериалов достаточно удобно проводить в рамках метода сильной связи, который хорошо зарекомендовал себя в расчетах систем из легких атомов.
Вследствие
трансляционной симметрии кристалла в
направлении векторов решетки
 любая
волновая функция в кристалле должна
удовлетворять теореме Блоха
любая
волновая функция в кристалле должна
удовлетворять теореме Блоха
 ,
(i = 1, 2, 3) (1)
,
(i = 1, 2, 3) (1)
где
 – трансляционная операция вдоль вектора
решетки, а
– трансляционная операция вдоль вектора
решетки, а
 - волновой вектор. Волновая функция Ψ
может быть разложена различными
способами. Этот метод имеет определенные
преимущества (они просто интегрируемы
(иногда и аналитически), точность зависит
только от числа использованных плоских
волн), но и не лишен недостатков: 1) большой
масштаб вычислений, 2) достаточно сложно
соотнести плоскую волну и атомную
орбиталь в кристалле. Другая форма Ψ,
которая удовлетворяет теореме Блоха
(1) — линейная комбинация атомных
орбиталей (ЛКАО) (в элементарной ячейке
или в атоме). Т.е., базисные функции
представляются в виде:
- волновой вектор. Волновая функция Ψ
может быть разложена различными
способами. Этот метод имеет определенные
преимущества (они просто интегрируемы
(иногда и аналитически), точность зависит
только от числа использованных плоских
волн), но и не лишен недостатков: 1) большой
масштаб вычислений, 2) достаточно сложно
соотнести плоскую волну и атомную
орбиталь в кристалле. Другая форма Ψ,
которая удовлетворяет теореме Блоха
(1) — линейная комбинация атомных
орбиталей (ЛКАО) (в элементарной ячейке
или в атоме). Т.е., базисные функции
представляются в виде:

Здесь
j
– индекс атомной орбитали,
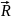 – позиция элементарной ячейки, количество
волновых функций в элементарной ячейке
обозначается как n,
что приводит к наличию n
волновых функций в кристалле для
заданного
.
N
– число элементарных ячеек. Элементарные
ячейки взвешиваются фазовым коэффициентом
– позиция элементарной ячейки, количество
волновых функций в элементарной ячейке
обозначается как n,
что приводит к наличию n
волновых функций в кристалле для
заданного
.
N
– число элементарных ячеек. Элементарные
ячейки взвешиваются фазовым коэффициентом
 .
Преимущества данного метода для
углеродных структур заключаются в том,
что он позволяет: 1) вывести формулы
физических свойств, 2) хорошо подходит
для легких атомов, 3) число базисных
функций n
может быть небольшим.
.
Преимущества данного метода для
углеродных структур заключаются в том,
что он позволяет: 1) вывести формулы
физических свойств, 2) хорошо подходит
для легких атомов, 3) число базисных
функций n
может быть небольшим.
Можно
получить квантование вектора
в зоне Бриллюэна
 , p
= 0, 1, … M–1.
M
=
, p
= 0, 1, … M–1.
M
=

Собственные
функции твердого тела описываются
линейной комбинацией (ЛК) базисных
функций
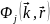 :
:

 .
.
Поскольку
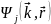 должны удовлетворять блоховской теореме
(1) суммирование проводится только для
одних и тех же
.
Собственные значения для состояний j
даются формулой:
должны удовлетворять блоховской теореме
(1) суммирование проводится только для
одних и тех же
.
Собственные значения для состояний j
даются формулой:
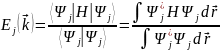 , (2)
, (2)
где
H
– гамильтониан в твердом теле. Подставляя
(1) в (2) получим:
 ,
где
,
где
 и
и
 называются матрицами переноса и
перекрытия соответственно. Минимизацией
энергии можно вывести т. н. секулярное
уравнение: det[H
– ES]
= 0, решение которого и дает дисперсионное
соотношение.
называются матрицами переноса и
перекрытия соответственно. Минимизацией
энергии можно вывести т. н. секулярное
уравнение: det[H
– ES]
= 0, решение которого и дает дисперсионное
соотношение.
Таким образом, алгоритм метода сильной связи выглядит следующим образом.
1. Выбрать элементарную ячейку и трансляционные вектора . Определить координаты атомов. Выбрать n орбиталей, которые учитываются в расчете.
2.
Определить зону Бриллюэна для данной
элементарной ячейки и вектора обратной
решетки
 .
Выбрать характерные точки и направления
зоны Бриллюэна.
.
Выбрать характерные точки и направления
зоны Бриллюэна.
3. Для каждого k посчитать матрицы и .
4. Решить секулярное уравнение и найти дисперсионное отношение E(k).
1.6.2. Расчеты зонной структуры углеродных нанотрубок методом сильной связи
В
1992 году было проведено несколько расчетов
на основе модели сильной связи для УНТ
и графена. Для проведения этих расчетов
элементарная ячейка графена была
выбрана, как показано на рис. 7, a.
В реальном пространстве трансляционные
вектора имеют координаты
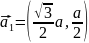 ,
,
 .
Вектора же обратной решетки равны
.
Вектора же обратной решетки равны
 .
.
|
|
Рис. 7. Элементарная ячейка и зона Бриллюэна графена. |
Рис. 8. Дисперсионное соотношение в графене в модели сильной связи. |
В обратной решетке выбрано три характерные точки Г, K и M. Решетка содержит два неэквивалентных атома С. В результате применения метода сильной связи к данной решетке при расчете π – связей было получено следующее выражение: |
|
Рис. 9. Дисперсия в графене с учетом σ – связей. |
 .
.
Соответствующее дисперсионное соотношение изображено на рис. 8. Если учитывать σ – связи, то можно получить более полное распределение электронов по энергиям (рис. 9).
Для расчета ОУНТ по методу сильной связи были использованы плоская элементарная ячейка (см. рис. 5) и соответствующая ей зона Бриллюэна (рис. #).
В результате расчетов ширины запрещенной зоны углеродных нанотрубок было получено т.н. правило 3k. Согласно этому правилу, УНТ с индексами хиральности (m, n) такими, что |m – n| ≠ 3k (где k – целое) обладают полупроводниковым типом проводимости, тогда как остальные обладают металлической проводимостью или нулевой запрещенной зоной.
|
|
Рис. 10. Элементарная ячейка ОУНТ (4, 2) (C – хиральный вектор, τ – трансляционный вектор). |
Рис. 11. Зона Бриллюэна ОУНТ дается отрезком WW’ (для ОУНТ(4, 2)). K1 и K2 – аналоги Ch и T в обратном пространстве. |
|
|
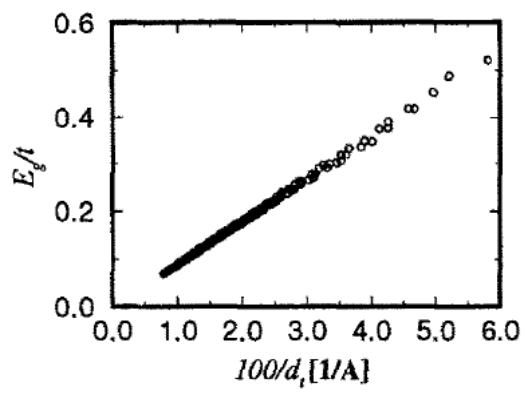
Рис. 12. Данные о запрещенной зоне ОУНТ по методу сильной связи: |
|
а) распределение нанотрубок по типу проводимости (темный значок – полупроводниковая, светлый – металлическая). |
б) ширина запрещенной зоны ОУНТ в зависимости от обратного диаметра в единицах интеграла переноса |t| ~ 2.5 эВ. |
Итоговые распределения УНТ по типам проводимости в зависимости от хиральности и радиуса приведены на рис. 12 (согласно методу сильной связи без учета эффектов кривизны).