Пример расчета
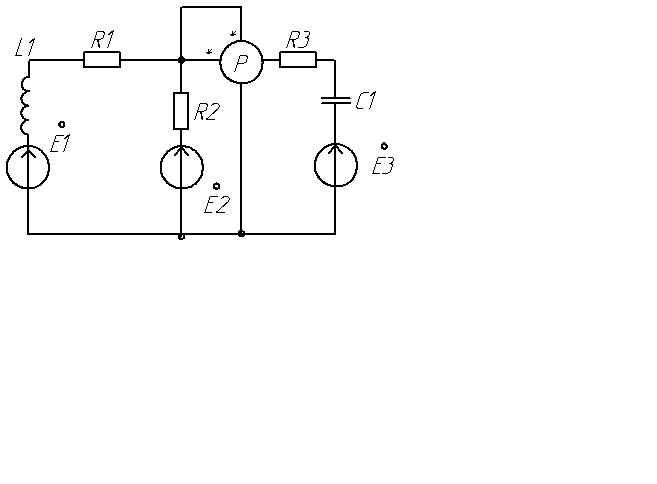
Пусть необходимо произвести расчет цепи (рис. 1) для следующих числовых значений параметров:
Em1 = 100 В, Em2 = Em3 = 0, = 90о, R1 = 200 Ом, R2 = 300 Ом, R3 = 0, L1 = 0,7 Гн,
С1 = 10 мкФ.
1. Находим реактивные сопротивления индуктивности L1 и емкости C1
(1)
Подставив в формулу (1) численные данные, получаем XC1 = 318 Ом, XL1 = 220 Ом.
2. Представим источник синусоидального напряжения в виде
где Em1 = 100 В, = 90o.
Для расчета цепи символическим методом необходимо представить источник в виде так называемого комплекса действующего значения
3. Обозначим токи İ1, İ2 и İ3, и выберем их направления, как показано на рис.2.
İ1
İ2
İ3
Рис. 2
3. Находим комплексное сопротивление цепи относительно зажимов источника Схема цепи при этом будет выглядеть, как показано на рис. 3.
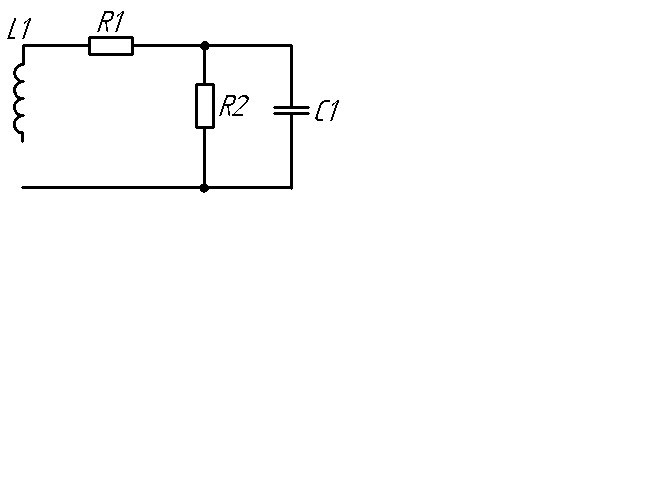
Рис. 2
Рис. 3
Комплексное сопротивление определяем по правилам для последовательного и параллельного соединения элементов
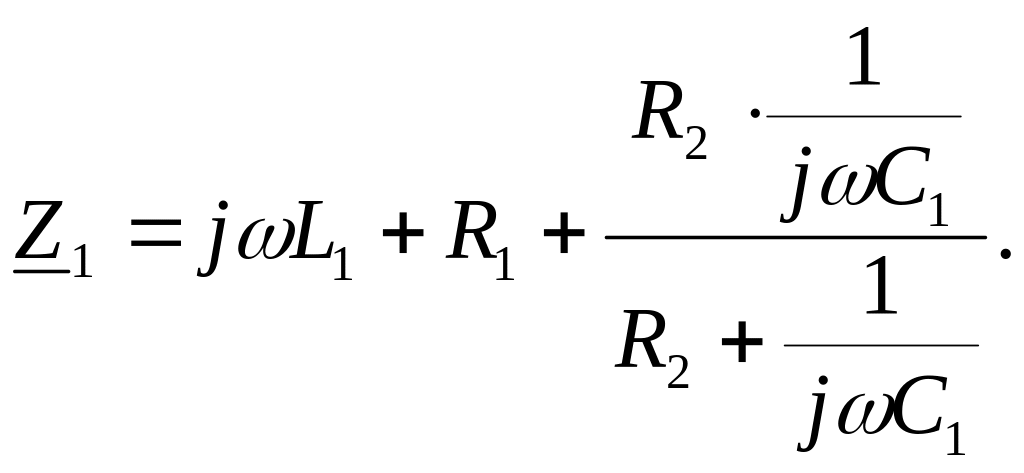(2)
Подставив в формулу (2) численные значения, получаем
4. Находим ток İ1
5. Находим комплексное сопротивление участка цепи, содержащего элементы R2 и C1
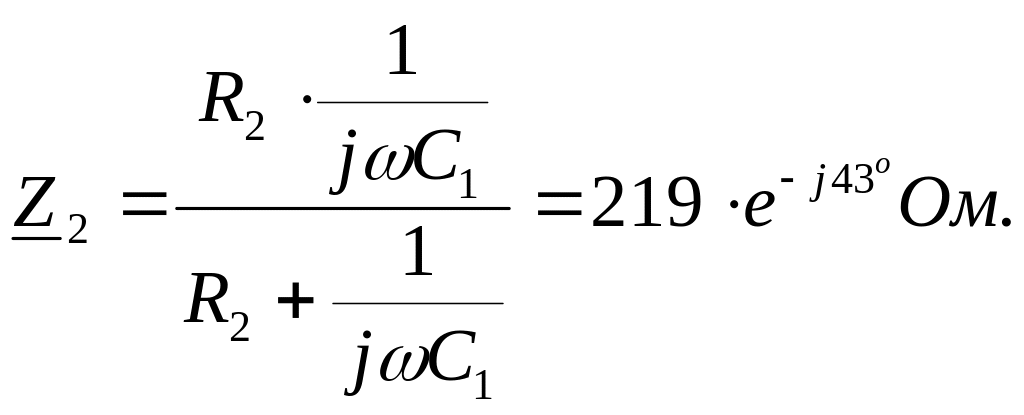
6. Находим падение напряжения на элементах R2 и C1
7. Находим токи İ2 и İ3
8. Методика построения векторной диаграммы токов и напряжений.
Для построения найдем напряжения
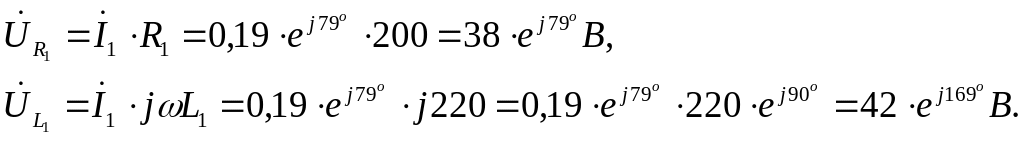
Выбираем масштабы по току и по напряжению mU = 10 В/см, mI = 0,05 А/см.
Определяем длины векторов:
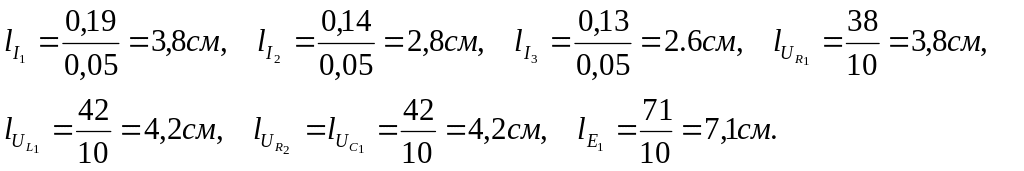
Откладываем вектора вышеуказанных величин на комплексной плоскости с соответствующими углами, как показано на рис.4.
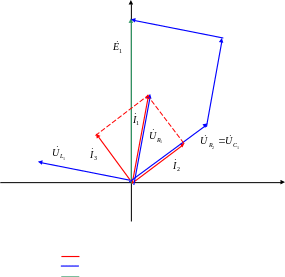
Рис. 4. Векторная диаграмма для токов и напряжений:
вектора токов
вектора напряжений
вектор ЭДС
Как видно из рис. 4, для данной цепи выполняются первый и второй законы Кирхгофа
9. Рассчитываем показания ваттметра. Для вычисления мощности в комплексной форме необходимо перемножить комплекс напряжения на сопряженный комплекс тока. Действительная часть полученного выражения будет соответствовать активной мощности, то есть представлять показания ваттметра.
Применительно к данной цепи полная мощность
В результате получаем
(3)
Поскольку действительная часть выражения (3) равна нулю, то и активная мощность в данном случае равна нулю
Действительно, нагрузкой для ваттметра является идеальная емкостная нагрузка С1, которая не потребляет активной мощности.