Домашнее задание
Найти интегралы:
№262.
.
Ответ:
.
№263.
.
Ответ:
.
№264.
.
Ответ:
.
№265.
.
Ответ:
.
№266.
.
Ответ:
.
№267.
.
Ответ: tg
x–x.
№268.
.
Ответ:
.
№269.
.
Ответ:
.
№270.
.
Ответ:
.
№271.
.
Ответ:
.
№272.
.
Ответ:
.
№273.
.
Ответ:
.
№274.
.
Ответ:
.
№275.
.
Ответ:
.
№276.
.
Ответ:
.
№277.
.
Ответ:
.
№278.
.
Ответ:
.
№279.
.
Ответ:
.
№280.
.
Ответ:
.
Дополнительные задания
Найти интегралы:
№281.
.
Ответ:
.
№282.
.
Ответ:
.
№283.
.
Ответ:
.
№284.
.
Ответ:
.
№285.
.
Ответ:
.
№286.
.
Ответ:
.
№287.
.
Ответ:
.
№288.
.
Ответ:
.
№289.
.
Указание.
Замена t=ctg
x. Ответ:
.
№290.
.
Ответ:
.
№291.
.
Ответ:
.
№292.
.
Ответ:
,
где t=tg
x.
№293.
.
Ответ: ln|tg
x|.
№294.
.
Ответ:
.
№295.
.
Указание. Замена ctgx=t.
Ответ:
.
№296.
.
Ответ: ln|sinx|-sinx.
№297.
.
Ответ:
.
Примерный вариан решения
индивидуального домашнего задания
Найти интегралы:
№18.
.
►
=
=
=
=
=
=
=
.◄
№19.
.
►
=
=
=
=
=
=
.◄
№20.
.
►
=
=
=
=
.◄
№38.
.
►
=
=
=
=
=
=
=
.◄
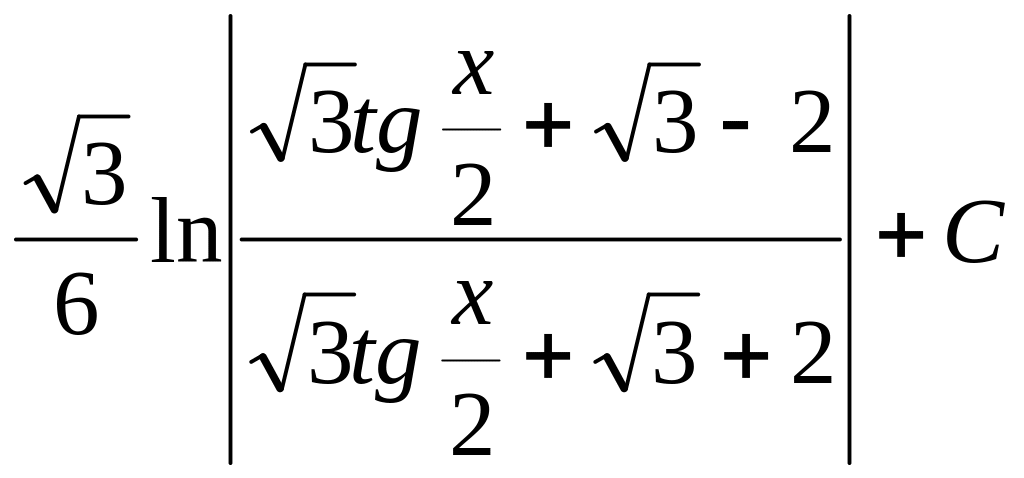№39.
.
►
=
=
=
=
=
=
=
.◄
№40.
►
=
=
=
=
=
=
=
=
=
=
.◄
Занятие 7
Интегрирование некоторых иррациональностей
Цели
Знать:
Основные приёмы интегрирования квадратичных иррациональностей.
Уметь:
Применять основные приёмы интегрирования квадратичных иррациональностей;
выделять полный квадрат из квадратного трёхчлена под знаком радикала;
применять дробно-линейную подстановку; тригонометрическую подстановку.
Интегралы вида:
(20)
называют неопределёнными интегралами от квадратичных иррациональностей.
Постановка задачи. Найти интеграл .
План решения.
Для нахождения интеграла следует:
Если числитель есть дифференциал подкоренного трёхчлена, то следует сделать замену
,
что приводит исходный интеграл к виду
.Если числитель не зависит от х, т.е. М=0, то под знаком радикала выделим полный квадрат из квадратного трёхчлена, в результате чего получим квадратный двучлен, в зависимости от знака а исходный интеграл сводится к одной из табличных формул
[11]
или
[12].
Если
,
то под знаком радикала выделив полный
квадрат, сделать подстановку
,
при этом исходный интеграл разбивается
на сумму двух интегралов.
Интегралы вида
, (21)
где R — рациональная функция; p,q,…,s,t — целые числа, находятся с помощью постановки
,
где m — наименьшее общее кратное чисел q,…,t.
Частные случаи:
1) если в интеграле (21) с=0, то он будет иметь вид
, (22)
где
;
2) если b=c=0, a=d=1, то интеграл (21) примет вид
. (23)
Интегралы вида (22) или (23) находятся с помощью подстановки
или
.
К интегралам от функций, рационально зависящих от тригонометрических функций, сводятся интегралы:
(24)
подстановкой
x=a sint; dx=a cost dt
или
x=a cost; dx=-a sint dt
(25)
подстановкой
x=a
tgt;
или
x=a
ctgt;
(26)
подстановкой
;
или
Интегралы вида:
(27)
Здесь
подынтегральная функция есть рациональная
функция относительно х и
.
Выделив под радикалом полный квадрат
и сделав подстановку
,
интегралы указанного вида приводятся
к интегралам вида:
,
,
.
Интеграл от дифференциального бинома
(28),
где a,
b — действительные
числа; m, n,
p — рациональные
числа, берутся, лишь в случае, когда одно
из чисел р,
или
— является целым.
Интеграл от дифференциального бинома сводится к интегралу от рациональной функции в трёх случаях:
когда р — целое число,
подстановка
,
где k — наименьшее
общее кратное дробей m
и n;
когда — целое число,
подстановкой
,
где s — знаменатель дроби
p;
когда — целое число,
подстановкой
,
где s — знаменатель дроби
р.
Во всех
остальных случаях интегралы вида
не выражаются через известные элементарные
функции, т.е. «не берутся».
Интеграл вида:
(29)
можно найти
подстановкой
.
№ 7. Найти
интегралы: 1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
.
►1)
=
=
=
=
=
=
=
=
;
2)
=
=
=
=
=
=
;
3)
=
=
=
=
=
=
=
;
4)
=
=
=
=
=
=
;
5)
=
=
=
=
=
=
=
=
.
Замечание.
Ответ можно упростить, если воспользоваться
тем, что
и
,
следовательно
=
;
6) Это интеграл от дифференциального бинома.
=
=
=
=
=
=
=
=
=
=
=
=
;
7)
=
=
=
=
=
.
Здесь учтено,
что
,
что подынтегральная функция определена
в интервале –1<x<1,
вследствие чего х-1<0 и t<0
и поэтому|t|=-t.
=
=
;
8)
=
=
=
=
=
=
=
=
=
=
.
Получили возвратный интеграл. Следовательно, имеем:
=
;
;
;
Учитывая, что t=x-1, получаем
.◄