Домашнее задание
Найти интегралы:
№187.
.
Ответ:
-ln|3-x|.
№188.
.
Ответ:
.
№189.
.
Ответ:
.
№190.
.
Ответ:
.
№191.
.
Ответ:
.
№192.
.
Ответ:
.
№193.
.
Ответ:
.
№194. . Ответ: .
№195.
.
Ответ:
.
№196.
.
Ответ:
.
№197.
.
Ответ:
.
Дополнительные задания
Найти интегралы
№198.
.
Ответ:
.
№199.
.
Ответ:
.
№200.
.
Ответ:
.
№201.
.
Ответ:
.
№202.
.
Ответ:
.
№203.
.
Ответ:
.
№204.
.
Ответ:
№205.
.
Ответ:
.
№206.
.
Ответ:
.
№207.
.
Ответ:
.
№208.
.
Ответ:
.
№209.
.
Ответ:
.
№210.
.
Ответ:
.
№211.
.
Ответ:
.
№212.
.
Ответ:
.
№213.
.
Ответ:
.
№214.
.
Указание.
Подстановка
.
Ответ:
.
№215.
.
Указание. Подстановка x-1=t.
Ответ:
.
№216.
.
Указание.
.
Ответ:
.
№217.
.
Указание.
Разложить знаменатель подынтегральной
дроби на множители:
=
=
=
.
Ответ:
.
№218.
.
Указание.
.
Ответ:
.
№219.
.
Указание. Замена t=x+2.
Ответ:
.
№220.
.
Указание.
Поделив числитель и знаменатель
подынтегральной дроби на х101,
сделать замену
.
Ответ:
.
Занятие 5 Интегрирование рациональных дробей вида
Цели
Знать:
правила разложения рациональных дробей на простейшие дроби;
правила интегрирования рациональных дробей.
Уметь:
выделять полный квадрат в квадратном трёхчлене;
интегрировать рациональные дроби.
Постановка
задачи. Найти интеграл
.
План решения.
Для нахождения интеграла следует:
Выделить в знаменателе полный квадрат, получим:
,
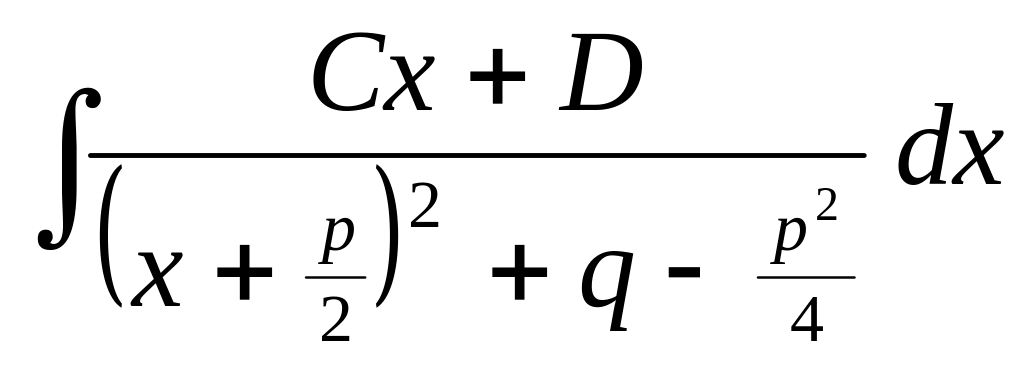причём
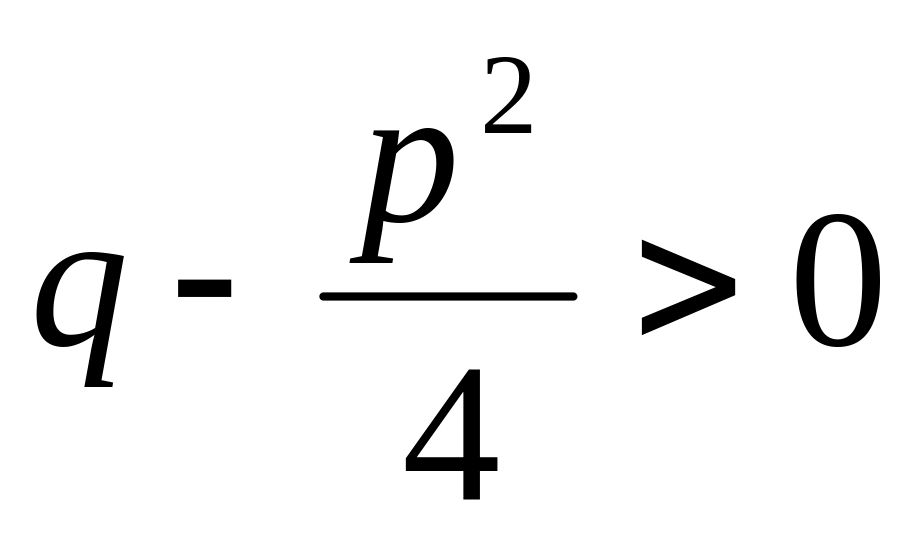.Сделаем подстановку
,
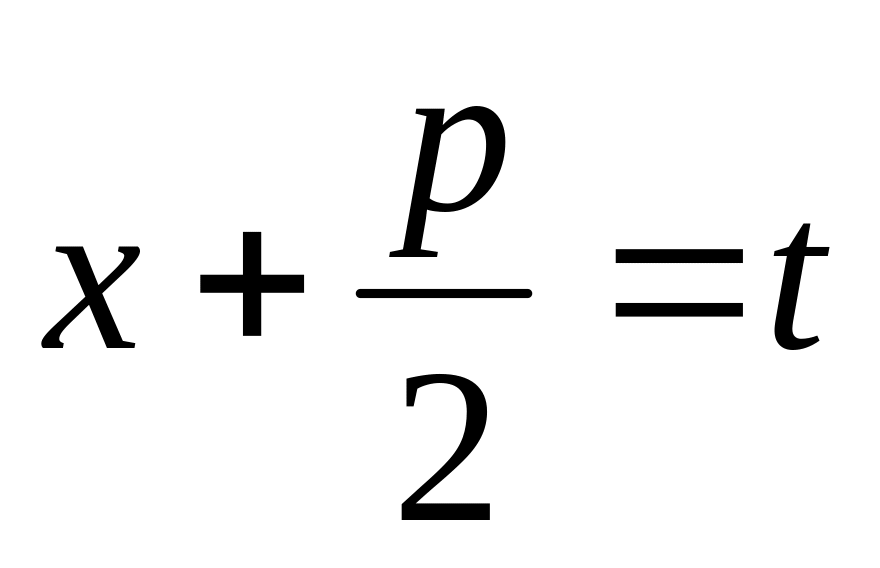тогда
,
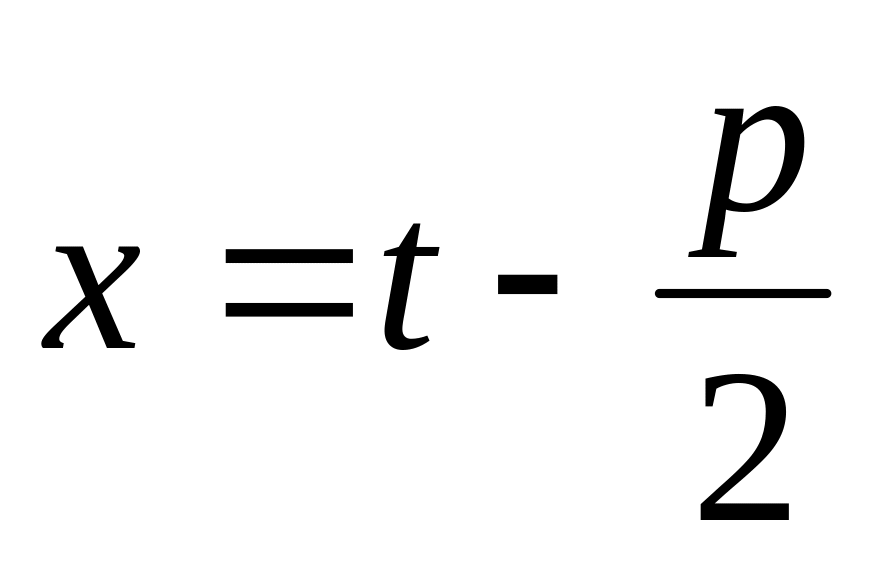dx=dt.
Положим
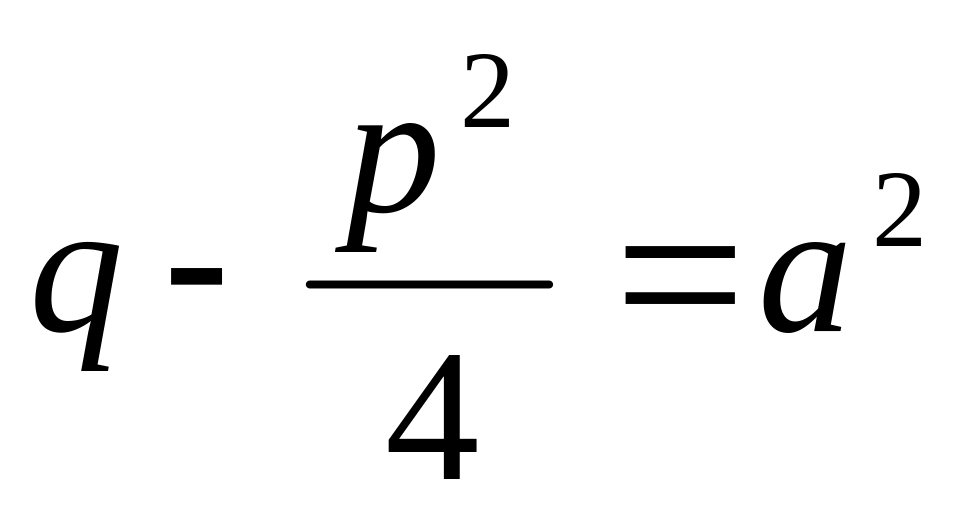.Запишем исходный интеграл:
=
Возвращаясь к исходной переменной, имеем:
=
=
.
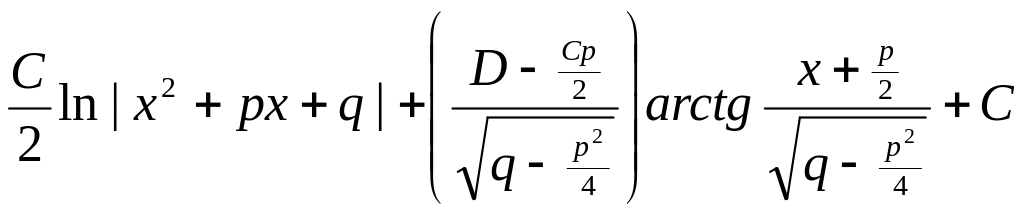№5. Найти
интегралы: 1)
;
2)
.
►1)
=
=
=
=
=
=
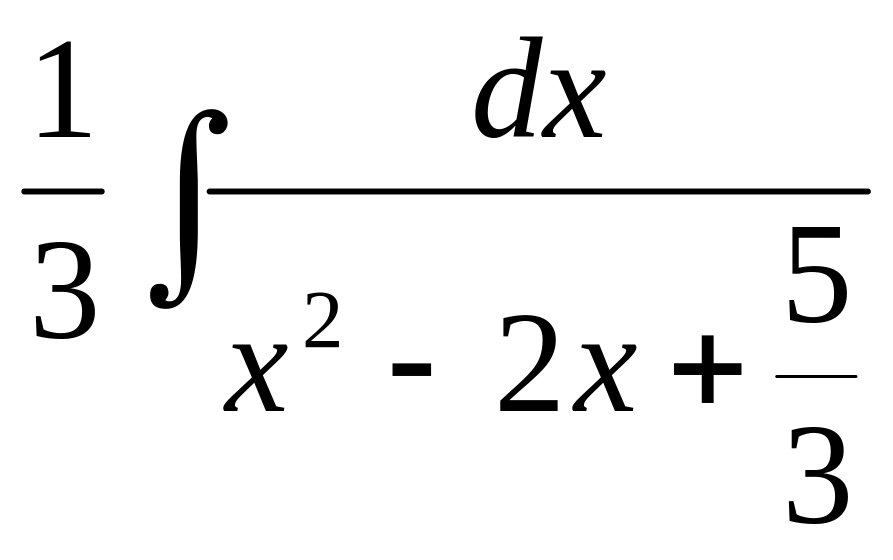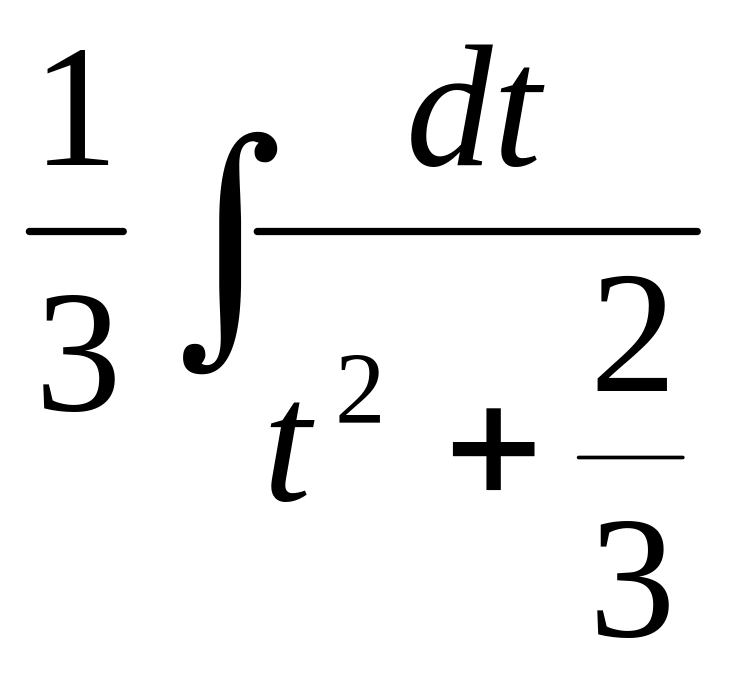+С=
;
2)
=
=
=
=
=
=
=
=
=
.◄
Аудиторное занятие
Найти интегралы:
№221.
.
Ответ:
.
№222.
.
Ответ:
.
№223.
.
Ответ:
.
№224.
.
Ответ:
.
№225.
.
Ответ:
.
№226.
.
Ответ:
.
№227.
.
Ответ:
.
№228.
.
Ответ:
.
№229.
.
Ответ:
.
Домашнее задание
Найти интегралы:
№230.
.
Ответ:
.
№231.
.
Ответ:
.
№232.
.
Ответ:
.
№233.
.
Ответ:
.
№234.
.
Ответ:
.
№235.
.
Ответ:
.
№236.
.
Ответ:
.
№237.
.
Ответ:
.
№238.
.
Ответ:
.
№239.
.
Ответ:
.
№240.
.
Ответ:
.
Дополнительные задания
Найти интегралы:
№241.
.
Ответ:
.
№242.
.
Ответ:
.
№243.
.
Ответ:
.
№244.
.
Ответ:
.
№245.
.
Ответ:
.
№246.
.
Ответ:
.
№247.
.
Ответ:
.