Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

неопред-интеграл.doc

Скачиваний:

Добавлен:

19.08.2019

Размер:

2.95 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

1. Метод сравнивания коэффициентов

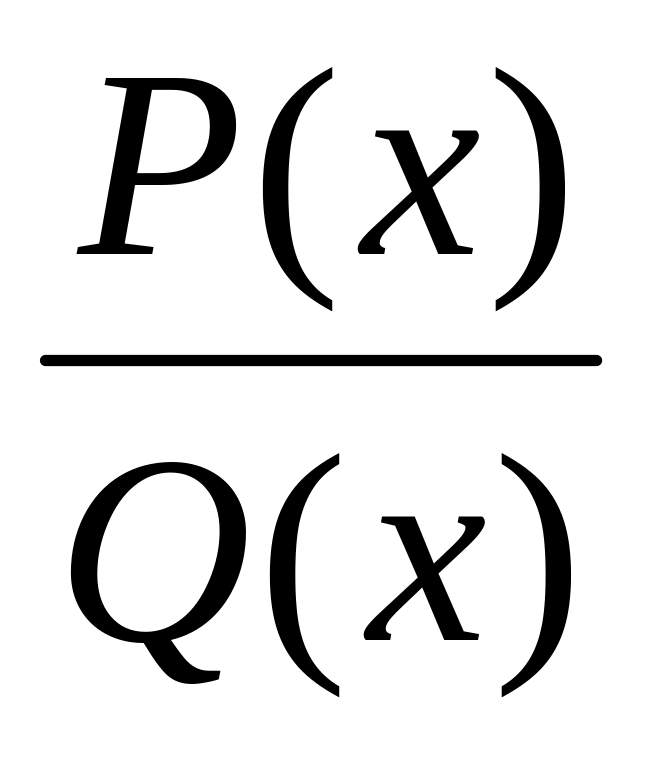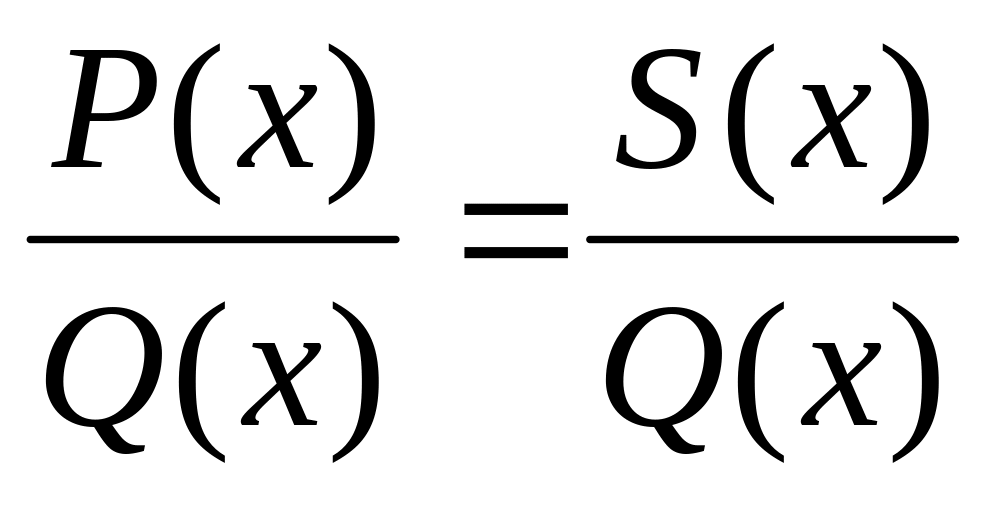Правильную дробь разложить на сумму простейших слагаемых. В результате получим тождество , где S(x) — многочлен с неопределёнными коэффициентами.
Так как в полученном тождестве знаменатели равны, то тождественно равны и числители, т.е. .
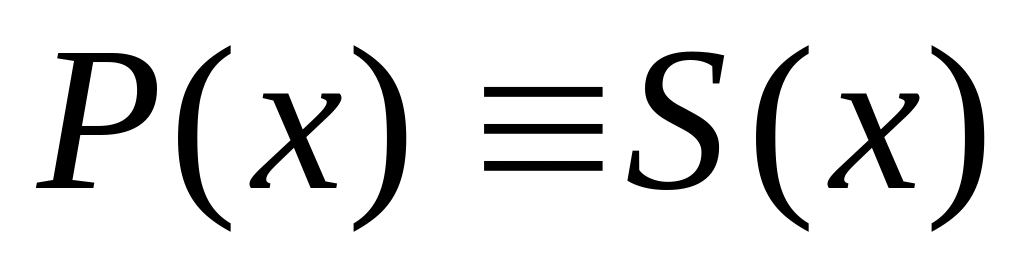Приравнивая коэффициенты при одинаковых степенях х в обеих частях тожества , получаем систему линейных уравнений, из которых и определяем искомые коэффициенты.

2. Метод частных значений аргумента

Правильную дробь разложить на сумму простейших слагаемых. В результате получим тождество , где S(x) — многочлен с неопределёнными коэффициентами.
Так как в полученном тождестве знаменатели равны, то тождественно равны и числители, т.е. .
Аргументу х придают конкретные значения столько раз, сколько неопределённых коэффициентов (обычно полагают вместо х значения действительных корней многочлена Q(x)).

Проинтегрировать многочлен и полученную сумму простейших дробей.

Если дробь простейшая, то воспользоваться соответствующей формулой:

= .

№4. Найти интегралы: 1) ; 2) ;

3) ; 4) .

►1) = ;

2) = = = ;

3) . Подынтегральное выражение — неправильная дробь. Разложим знаменатель дроби на простые действительные множители. Имеем

Представим дробь в виде простейших рациональных дробей:

Корень х=2 имеет кратность, равную двум, поэтому в разложении ему соответствуют два слагаемых. Теперь приведём это разложение к общему знаменателю, а затем, освободившись от него, получим

;

Из этого тождества определим коэффициенты А, В, С методом сравнивания коэффициентов: приравняв коэффициенты при одинаковых степенях х слева и справа, получаем систему из трёх уравнений с тремя неизвестными

, , .

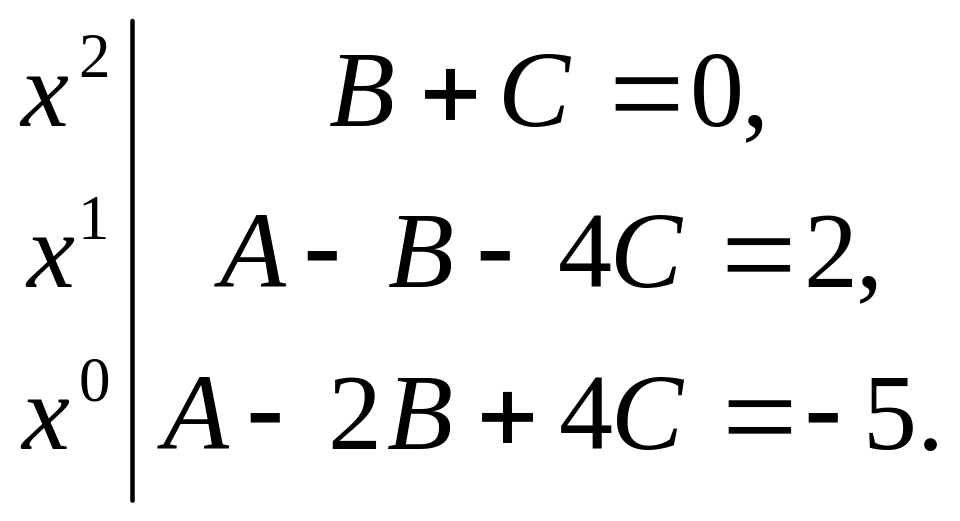
Окончательно имеем:

Следовательно, =

= = .

4) . Подынтегральная дробь — неправильная. Исключим целую часть, для этого путём деления многочлена на многочлен данную дробь представим в виде суммы целой рациональной функции и правильной дроби: