Мінімізувати цільову функцію

Z (f) = (T  V +  D_ij  _ij -  d_ij  _ij)  min  (1.26)

за умови, що

f_ij +  _ij -  _ij =  C_ij для  (i, j)    A, (1.27)

 f_1j -  V = 0 i  = 1, (1.28)

(f_ij -  f_ji) = 0 для  i = 2,..., n -1, (1.29)

-  f_in  +  V  = 0   i =  n,  (1.30)

f_ij, _ij, _ij  0 для (i, j)    A. (1.31)

Подвійні обмеження є рівністю, оскільки змінні в основній задачі в явному вигляді не обмежені по знаку.

На основі математичної структури двоїстої задачі двоїсті змінні f_ij можна розглядати як потоки в мережі з обмеженою пропускною спроможністю. Умови (1.28  1.30) відповідають обмеженням потоку для джерела, проміжних і кінцевого подій відповідно.

Так, обмеження (1.29) відповідає відомим обмеженням на збереження потоку в проміжних вузлах (типу Г.Р. Кирхгофа).

Використовуючи умови доповнюючої нежорсткості для задачі лінійного програмування, можна вивести наступні результати, які повинні виконуватися для оптимального рішення 161:

 T_i -  T_j +  X_ij < 0, f_ij = 0,

 T_i -  T_j +  X_ij = 0, f_ij > 0,

якщо  X_ij =  D_ij, то   _ij > 0;

якщо  X_ij =  d_ij, то  _ij > 0; (1.32)

якщо  X_ij <  D_ij, то  _ij = 0;

якщо  X_ij >  d_ij,  то   _ij = 0.

Двоїсті змінні _ij, _ij не можуть бути одночасно позитивними, оскільки D_ij  d_ij.

У обмеженні f_ij + _ij -  _ij = C_ij ненегативні значення _ij і  _ij визначаються по формулах:

_ij =  C_ij -  f_ij   при  _ij = 0;

_ij =  f_ij -  C_ij   при   _ij = 0. (1.33)

Т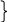 ому  _ij =  max  [0, C_ij -  f_ij]   при  _ij = 0,

_ij =  max [0, f_ij - C_ij]     при _ij = 0.

При дослідженні всіх можливих значень f_ij, _ij, _ij можна виділити три випадки:

1.  _ij > 0,  _ij = 0,  0   f_ij  C_ij, X_ij =  D_ij;

2. _ij = 0,   _ij = 0,   f_ij =  C_ij,  d_ij < X_ij < D_ij; (1.34)

3. _ij = 0,  _ij > 0,   f_ij >  C_ij,   X_ij =  d_ij.

Для кожного випадку з урахуванням умов доповнюючої нежорсткості знаходимо умови оптимальності.

1. 0 <  f_ij <  C_ij і T_i -  T_j +  D_ij = 0 або

f_ij = 0 і  T_i -  T_j +  D_ij < 0; (1.35)

2. f_ij =  C_ij і  T_i -  T_j +  X_ij = 0,  d_ij  X_ij  D_ij; (1.36)

3. C_ij <  f_ij <  і  T_i -  T_j +  d_ij = 0. (1.37)

Введемо наступні додаткові позначення:

 a^’_ij =  T_i -  T_j +  D_ij  резерв критичності;

 a^”_ij =  T_i -  T_j +  d_ij  резерв скорочення; (1.38)

_ij =  T_i -  T_j +  X_ij.

Умови оптимальності для кожного випадку можна записати в іншому вигляді:

В ипадок 1: 0 <  f_ij <  C_ij    a'_ij = 0, 

Випадок 2:  f_ij =  C_ij і  X_ij = 0, (1.39)

Випадок 3:  C_ij <  f_ij <   і  a"_ij = 0. 

За допомогою алгоритму послідовно визначаються f_ij  і  T_i (T_j), що задовольняють умовам (1.39) для убуваючих значень  T_n, після чого шукані невідомі визначаються по формулі 2

X_ij =  min  (D_ij, T_j -  T_i ). (1.40)