ФГОУ ВПО «КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

КАФЕДРА ФИЗИКИ

ЛАБОРАТОРНАЯ РАБОТА № 5

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА И МОМЕНТОВ ИНЕРЦИИ ТВЁРДЫХ ТЕЛ НА УСТАНОВКЕ «КРУТИЛЬНЫЙ МАЯТНИК»

Методическое указание к выполнению лабораторной работы по курсу общей физики для студентов инженерно-технических специальностей

Калининград

2008

ОГЛАВЛЕНИЕ

стр.

I. ВВЕДЕНИЕ 1

1.1. Общие сведения о деформации тел при кручении и моменте сил

упругих деформаций нитей в установках типа крутильных весов и

крутильного маятника 1

1.2. Вывод уравнения крутильных колебаний и методика определения

коэффициента кручения 4 1.3. Определение моментов инерции тел относительно главных и парал-

лельных осей 7

2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 9

2.1. Экспериментальная часть 9

2.2. Общие указания по подготовке и проведению измерений. 11

2.2.1. Подготовка 11

2.2.2. Измерения 12

2.3. Экспериментальные задания и обработка результатов 13

Задание № I. Измерение коэффициента кручения и модуля сдвига

cтальногопровода 13

Задание № 2. Измерение момента инерции рамки крутильного

маятника 15

Задание № 3. Измерение моментов инерции тел относительно главных

осей 15 Задание № 4. Измерение моментов инерции тел относительно оси, не

проходящей через центр масс 17

ВОПРОСЫ ДЛЯ ПРОВЕРКИ 18

ПРИЛОЖЕНИЕ. Главные оси и главные моменты инерции симметричных

однородных тел 19 СПИСОК ЛИТЕРАТУРЫ 20

ЦЕЛЬ РАБОТЫ

1. Изучение характеристик крутильных колебаний и определение коэффициента кручения в экспериментальной установке "кру­тильный маятник".

2.Измерение модуля сдвига стального провода.

3.Измерение главных моментов инерции твёрдых тел разной формы.

4.Измерение моментов инерции твёрдых тел относительно оси, не проходящей через центр масс тела. Изучение теоремы Штейнера о параллельных осях.

I. Введение

1.1. Общие сведения о деформации тел при кручении и моменте сил упругих деформаций нитей в установках типа крутильных весов и крутильного маятника.

Крутильный маятник по своему конструктивному устройству анало­гичен крутильным весам. Различие, однако, в том, что весы использу­ются в статическом режиме равновесия, а маятник применяется в ди­намическом режиме. При этом детали его конструкции вращаются, пери­одически изменяя направление поворота.

Простейшая конструкция крутильных весов (и крутильного маятника) представляет собой подвес на вертикальной нити, на свободном конце которой закреплена симметричная горизонтальная штанга или иное приспособление (например, рамка для установки изучаемых тел). С целью лучшей стабилизации оси поворота часто применяют растяжку, т.е. натянутые и закреплённые на концах две нити. В средней части располагается штанга либо рамка с боковыми рычагами (см. рис.1).

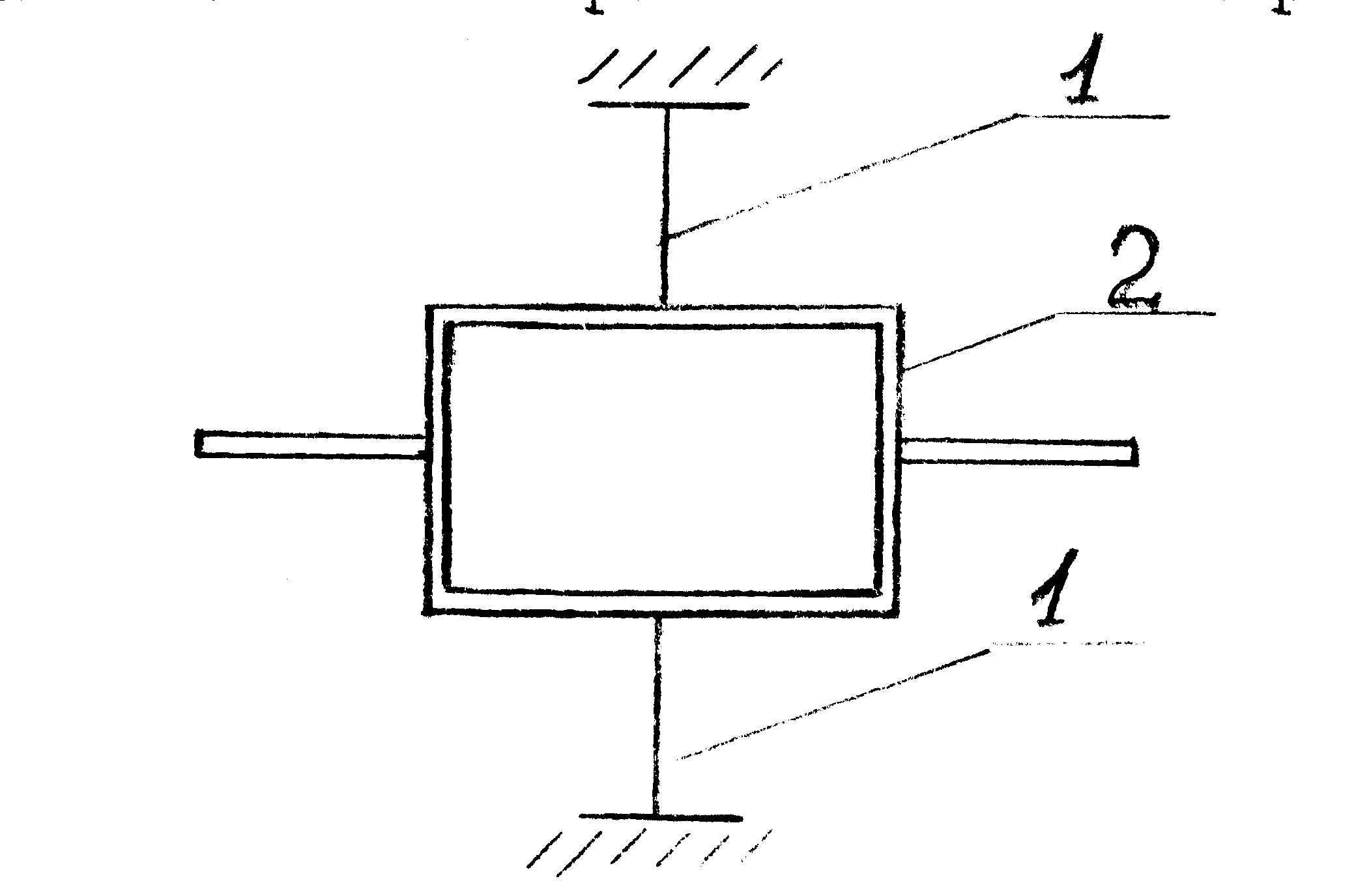
Рис.1

I – нити, 2 - рамка с рычагами

Если к рычагам рамки приложить горизонтальную силу, тогда нить, закреплённая на другом конце, начинает закручиваться. При закрутке нити происходят деформации сдвига её слоёв и возникает момент упру­гих сил, препятствующий повороту и стремящийся вернуть нить в исхо­дное, недеформированное состояние.

При излишне большой закрутке деформация нити становится неупругой (пластической), т.е. после снятия внешней силы, приложенной к рычагу, нить не возвращается в исходное состояние. Все измерения на крутильных весах (и маятнике) требуется выполнять в условиях уп­ругой деформации при ограниченном угле закрутки нити. В этом случае по углу закрутки, т.е. по углу поворота рычага (и рамки) на крутильных весах можно определить момент внешних сил Мвн, приложенных к рычагам.

В условиях равновесия имеем:

М вн = М_кр , (1)

где Мкр. - момент сил упругой деформации закрученной нити, равный:

; (2)

(Единица измерения «радиан», как дополнительная в системе СИ, размерности не имеет).

В формуле (2) величина φ называется коэффициентом кручения, который определяется для каждой данной конструкции в зависимости от материала, радиуса и длины нити следующим выражением:

, (3)

где r - радиус нити; - длина нити; G - модуль сдвига материала нити. Размерность коэффициента , согласно формуле (2), равна = Н∙м/рад.= Н∙м.

Выражение (3) определяет коэффициент кручения для подвеса на одной нити. В случае растяжки на двух разных нитях действуют два момента упругих сил, равные:

; , (4)

где:

(5)

Суммарный момент сил упругой деформации растяжки на двух разных нитях равен:

М_кр = М₁ + М₂ (5а)

или

(5б)

Если нити растяжки изготовлены из одного материала, имеют одинако­вые радиусы, но разную длину, тогда выражение (5б) преобразуется к виду:

(6)

В формулах (5б) и (6) коэффициент при угле поворота явля­ется коэффициентом кручения для данной, конкретной установки и обо­значается аналогично формуле (2). Для растяжки на двух нитях из одинакового материала при равных радиусах получаем:

(7)

ПРИМЕЧАНИЕ I. Формулы (2), (4), (5б) и (6) определяют величину (мо­дуль) момента сил упругой деформации кручения без учёта знака проекции вектора момента этих сил.

ПРИМЕЧАНИЕ 2. Нити подвесов и растяжек для крутильных весов и маят­ников изготавливают из тонкого стального провода специальных марок. Для особо точных приборов применяются кварцевые нити.

ПРИМЕЧАНИЕ 3. Вывод формулы (3) для коэффициента кручения изучается в курсе "Сопротивление материалов". Модуль сдвига G наряду с модулем Юнга Е являются справочными данными как модули упругос­ти для каждого сорта материалов. Сведения об этих модулях необходи­мы для расчёта прочности и жёсткости любой конструкции машин, двигателей, строительных сооружений и т.д.

Модуль Юнга определяется как отношение плотности силы F_N, дей­ствующей по нормали к сечению, к величине относительной деформа­ции растяжения материала , т.е. равен E=F_N/ ; размерность [ Е ] = Н/м² . Модуль сдвига G определяется как отношение плотности силы Fτ , действующей по касательной к сечению, к величине угла скоса рёбер куба, основание которого закреплено и остается не­подвижным, а противоположная грань, к которой приложена касательная сила с плотностью Fτ, сдвигается. Формула для величины G имеет вид:

G = Fτ / ; размерность [G] = Н/м² •рад. = Н/м².

Модули Е и G для каждого материала определяются опытным методом. Для измерения величины Е существуют специальные установ­ки, где материал подвергается испытаниям на сжатие и растяжение. Измерение величины G выполняется обычно методом кручения, т.е. для расчётов применяется формула типа (3), где коэффициент кручения измеряется независимо также на основе опытных данных.

Понятие о модулях как характеристиках упругих свойств матери­алов при малых деформациях было введено в конце XVIII- начале XIX веков. В этот же период С. Пуассоном было теоретически вычислено соотношение между модулями Е и G , имеющее вид:

, где - коэффициент Пуассона, который равен отношению относите­льного поперечного сжатия образца материала к соответствующему отно­сительному продольному удлинению. Например, для многих металлов коэффициент 0,3.

Устройства, использующие подвесы (или растяжки) на тонких нитях, были и остаются одними из наиболее чувствительных приборов для измерения сил. Применяя установку типа крутильных весов, Ш. Кулон в 1785 г. исследовал взаимодействие электрически заряженных тел и ус­тановил закон, определяющий силу электростатического взаимодействия; Г. Кавендиш в 1798 г. измерил силу гравитационного притяжения двух небольших свинцовых шаров и впервые определил величину гравитацион­ной постоянной в законе всемирного тяготения; П.Н. Лебедев в 1899 г. экспериментально доказал, что свет оказывает давление на твёрдые тела.

Полезно отметить, что наиболее точные измерения коэффициентов кручения в особо чувствительных крутильных весах выполняются методом крутильных колебаний, т.е. с использованием той же установки в динамическом режиме крутильного маятника.

1.2. Вывод уравнения крутильных колебаний и методика определения коэффициента кручения.

Показанная на рис.1 рамка на растяжке из двух нитей может на­ходиться в состоянии покоя сколь угодно большое время. Однако, если рамку вывести из состояния покоя, например, повернуть на некоторый угол в пределах упругой деформации нитей и затем отпустить, тогда рамка начнёт периодически поворачиваться то в одну, то в другую стороны, вращаясь вокруг оси, проходящей через нити. Такая система называется крутильным маятником. Получим уравнение движения этой системы и покажем, что оно имеет вид известного в теории урав­нения свободных гармонических колебаний, которые в данной установке называются крутильными колебаниями.

Пренебрегая сопротивлением воздуха, считаем, что вращение рам­ки происходит только под действием момента сил упругой деформации закручиваемых нитей. Обозначим момент инерции рамки относительно оси вращения J₀ и запишем уравнение вращательного движения рам­ки под действием момента сил М_кр :

J₀ ∙ ε = М_кр (8)

Здесь ε и М_кр - проекции векторов углового ускорения рамки и момента сил упругой деформации на ось координат, проходящую через ось вращения.

С учётом направлений соответствующих векторов и выражений для ε и М_кр запишем (8) в виде дифференциального уравнения:

(9)

Здесь: - вторая производная по времени от угла поворота рамки, определяющая её угловое ускорение ; - коэффициент кручения, определяемый формулой (7) для растяжки на двух нитях раз­ной длины, изготовленных из стали одной марки с одинаковыми радиусами (такие нити используются в установке настоящей лабораторной работы). В установках, применяемых в качестве крутильного маятника, коэффициент иногда называют коэффициентом жёсткости.

Уравнение (9) преобразуется к более наглядной канонической форме, позволяющей сразу найти его решение, т.е. функцию , определяющую зависимость угла поворота от времени. Для этого надо перенести все члены (9) в левую часть, разделить на коэффициент при второй производной по времени и ввести обозначение: . Получен­ное таким способом уравнение имеет вид:

+ (10)

Уравнение типа (10) называется уравнением свободных гармонических колебаний, т.к. решение этого уравнения

(11)

показывает, что угол поворота периодически изменяется с течением времени. Значение определяет максимальный угол поворота (амплитуду); называется собственной циклической частотой колебаний и определяет число одинаковых состояний системы за время 2 сек; - начальная фаза колебаний; - время.

Примечание. Колебаниями называются периодические изменения состоя­ния системы при условии, что данная система обладает собственной циклической частотой и состоянием с минимальной потенциальной энер­гией.

Период колебаний Т₀, т.е. интервал времени между двумя ближайшими одинаковыми состояниями системы, определяется формулой:

(12)

Отметим, что при исследовании крутильного маятника уравнение (10) называется уравнением крутильных колебаний, т.к. период колебаний определяется формулой:

, (13)

где - коэффициент кручения, зависящий только от параметров нитей исследуемой установки.

Рассмотрим теперь методику определения коэффициента кручения с помощью крутильных колебаний. Согласно формуле (13) период коле­баний зависит от момента инерции, если коэффициент кручения постоянный.

Обычно момент инерции рамки нельзя вычислить теоретически с достаточной точностью, т.к. её детали имеют разную конструктивную форму и массу. Следовательно, если выполнить измерение периода ко­лебаний с одной рамкой и рассматривать формулу (13) в качестве уравнения для определения величины , то в этом уравнении будут две неизвестные: и . Однако это уравнение можно дополнить вторым уравнением, измеряя период колебаний рамки с дополнительным грузом, момент инерции которого известен (обычно такой груз имеет форму однородного цилиндра с известными массой и радиусом, при этом цилиндр устанавливается строго на оси вращения маятника).

Обозначая известный момент инерции добавочного груза , период колебаний рамки с грузом , имеем:

(14)

Возводя в квадрат выражения (13) и (14) и затем вычитая первое из второго, получим:

(15)

Из (15) находим коэффициент кручения:

(16)

Периоды колебаний Т₀ и Т₁ измеряются в опыте. Описанный здесь метод применялся для определения коэффициентов в установках, на которых выполнялись отмеченные выше классические эксперименты.

1.3. Определение моментов инерции тел относительно главных и параллельных осей.

Моменты инерции являются одной из важнейших характеристик твё­рдых тел, т.к. определяют инертные свойства тел при поворотах (вра­щениях) в пространстве. Повороты (вращения) могут происходить относительно различных осей и соответствующие этим осям моменты инерции тел обычно имеют разные значения.

Теорией и опытом доказано, что все твёрдые тела (любой формы) обладают тремя особыми взаимно-перпендикулярными осями, пересекаю­щимися в центре масс. Эти оси называются главными осями тела ввиду их примечательных свойств, описанных в литературе (см. Приложение).

Моменты инерции тел относительно главных осей принято называть главными моментами инерции, для однородных симметричных тел глав­ные моменты инерции легко вычисляются способом интегрирования. Та­кие моменты инерции тел простейших геометрических форм приводятся в справочной литературе (см. Приложение). При известных главных моментах инерции можно рассчитать моменты инерции тел относительно любых других осей. Наиболее просто такие расчёты выполняются для осей, параллельных главным осям (с применением теоремы Штейнера).

На практике, однако, часто применяются вращающиеся неоднород­ные тела сложной формы (например, гребные винты судов, роторы тур­бин, роторы электродвигателей и т.п.). Моменты инерции таких тел относительно заданных осей определяют опытным методом с помощью различных экспериментальных установок, где исследуемые тела совер­шают вращательное движение.

Наиболее точные измерения моментов инерции выполняются на ус­тановках типа физического и крутильного маятников.

Для измерений моментов инерции относительно осей, проходящих через центр масс тела, исследуемое тело устанавливают на платформе крутильного маятника (закреплённой, например, в рамке, показанной на рис.1). Заданную ось тела совмещают с осью вращения маятника и затем измеряют период колебаний Т.

Обозначая момент инерции рамки , (который можно найти в предварительном опыте при известном коэффициенте кручения ), запишем формулу для периодаколебаний:

(17)

Здесь - неизвестный момент инерции исследуемого тела.

Возводя (17) в квадрат, получаем:

(18)

В данной лабораторной работе формула (18) применяется для оп­ределения главных моментов инерции тел разной формы. Для однородных симметричных тел результаты измерений можно сравнить с резуль­татами расчётов моментов инерции по формулам, данным в Приложении.

Измерения моментов инерции относительно параллельной оси на крутильном маятнике следует выполнять с использованием двух одина­ковых тел. Исследуемые тела необходимо установить на платформе вну­три рамки симметрично, на одинаковых расстояниях заданных осей тел от оси вращения маятника (см. рис.2).

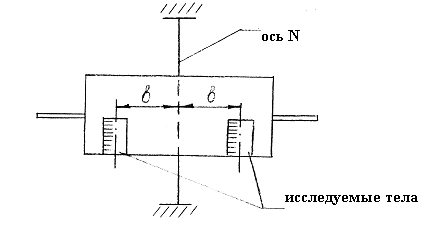
Рис. 2.

По теореме Штейнера момент инерции тела J_N относительно не­которой оси N , не проходящей через центр масс тела, равен сумме момента инерции тела J_c относительно оси, проходящей через центр масс тела параллельно заданной оси N , и произведения , где - масса тела, - расстояние между параллельными ося­ми.

(19)

В крутильном маятнике осью N является ось вращения маятника, проходящая через нити растяжки (показана на рис.2). Параллельные оси, проходящие через центры масс тел на расстоянии от оси N , также показаны на рис.2.

Суммарный момент инерции конструкции (рис.2) равен , где - момент инерции рамки. Период колебаний маятника:

(20)

Возводя (20) в квадрат, получаем:

(21)

Выражение (21) позволяет определить момент инерции для тела любой формы. Если момент инерции известен (для однород­ного симметричного тела), можно сравнить результаты измерения и расчёта с помощью формул (19) и (21).