9

При решении различных инженерных задач часто возникает необходимость в решении алгебраических или трансцендентных уравнений вида

(1)

где F(x) - некоторая непрерывная на отрезке [a, b] функция.

Сложность решения трансцендентных уравнений состоит в том, что они не имеют аналитических выражений для своих корней. Корни таких уравнений приходится искать приближенно, с некоторой степенью точности. На практике широко применяются следующие численные методы решения трансцендентных уравнений:

• метод последовательных приближений (простых итераций);

• метод Ньютона;

• модифицированный метод Ньютона;

• метод секущих;

• метод половинного деления (иначе - дихотомии, или бисекции).

Указанные методы отличаются расчетными формулами, однако существо их одинаково: при решении каждым из них происходит последовательное, шаг за шагом, уточнение значения корня от первоначального грубого приближения (или двух пер­во­на­чальных, как в методе секущих).

Важным условием реализации численного метода является правильное задание первого приближения. Дело в том, что при произвольном значении первого приближения, если выбор его не подчинить определенным правилам, велика вероятность того, что процесс вычислений будет расходящимся (т.е. каждое последующее значение будет все дальше и дальше от первого приближения).

Оценка первого приближения выходит за рамки данной работы. Предполагается, что задан отрезок, на котором уравнение имеет один корень, и в качестве первого приближения может быть взято любое число, принадлежащее данному отрезку.

Для реализации приближенного метода определения корней необходимо уравнение (1) представить в виде:

x = f( x ) (2)

Данное преобразование зависит от конкретного вида функции F(x) и как правило не вызывает особых затруднений. Если выражение (1) не содержит x в первой степени, то самый простой способ приведения его к виду (2) состоит в прибавлении к обеим частям величины x:

x = F(x) + x, (3)

т.е. f(x) = F(x) + x.

Рассмотрим алгоритмы указанных численных методов.

Метод простых итераций

В методе простых итераций приближения организуются по правилу:

x_k+1= f(x_k), где k = 0, 1, 2, 3, ... , (4)

причем задается начальное (нулевое) приближение x₀. При известном начальном приближении определяется первое приближение, затем второе, третье и т.д. до тех пор, пока не будет достигнута требуемая точность (т.е. разность между двумя последовательными приближениями не станет пренебрежимо малой).

Геометрическая интерпретация метода простых итераций представлена на рис.1 (для случая, если первое приближение лежит справа от истинного значения корня). Очевидно, что корнем уравнения является абсцисса точки пересечения двух графиков: y=x и y=f(x).

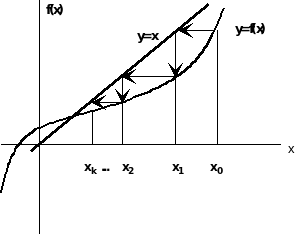
Рис.1.

Метод Ньютона

Алгоритм метода Ньютона строится исходя из представления функции F(x) в окрестности некоторой точки x* (предполагаемого корня уравнения), принадлежащей отрезку [a, b], в следующем виде:

F(x_k+1) = F(x_k) + (x_k+1 - x_k)* F ^(x_k ) (5)

Исходя из равенства F(x)=0 и в соответствии с (5) (k+1)-e приближение определяется по правилу:

, k=0,1,2,... (6)

Метод Ньютона иначе называется методом касательных (рис.2), поскольку для того, чтобы найти (k+1)-e приближение надо через точку x_k провести вертикальную прямую до пересечения с кривой F(x), затем провести касательную до пересечения с осью абсцисс (точка x_k+1), из точки x_k+1 - вновь вертикальную прямую до пересечения с F(x) и т.д.

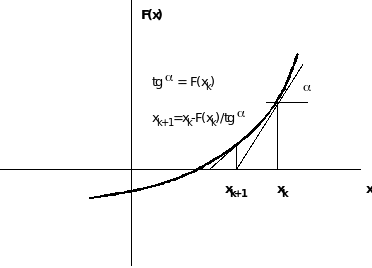
Рис.2

При программной реализации метода Ньютона приходится многократно вычислять первую производную функции F(x). Чтобы избежать этого, применяют модифицированный метод Ньютона, при котором производная вычисляется один раз в некоторой точке x*, принадлежащей отрезку [a, b]. Алгоритм модифицированного метода Ньютона реализуется при помощи следующего выражения:

, где k = 0, 1, 2, ... (7)

В разделе математики "Численные методы" доказывается, что если процесс, реализуемый по выражению (6) на отрезке [a, b] сходится, то и процесс, реализуемый по выражению (7), также сходится.

Метод секущих

Этот метод получается из метода Ньютона (6) заменой производной частным

,

вычисленным по известным значениям x_k-1 и x_k (указанные значения считаются известными, так как ищется (k+1)-е. приближение, а k-е и (k-1)-е найдены на предыдущих этапах вычислений).

Алгоритм метода секущих реализуется на основе следующего выражения:

, где k = 1, 2, 3, ... (8)

Как видно из (8), алгоритм метода секущих является двухшаговым, т.е. новое приближение x_k+1 определяется двумя предыдущими приближениями: x_k и x_k-1.

Геометрическая интерпретация метода секущих представлена на рис.3. Через точки A_k-1(x_k-1, F(x_k-1)) и A_k(x_k, F(x_k)) проводится прямая до пересечения с осью абсцисс. Это есть значение нового приближения x_k+1. Далее через точки A_k(x_k, F(x_k)) и A_k+1 (x_k+1, F(x_k+1)) проводится новая прямая и так далее до тех пор, пока разность между двумя соседними приближениями (x_k+1 и x_k) по абсолютной величине не станет меньше допустимой погрешности.

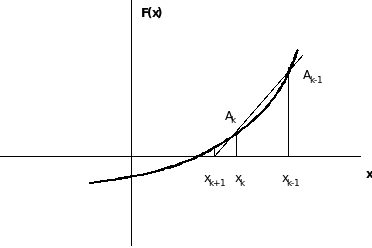
Рис.3

Метод половинного деления

Метод половинного деления (бисекции, дихотомии) является более устойчивым, чем рассмотренные выше. Существо его состоит в следующем.

Предполагается, что на отрезке [a, b] уравнение (1) имеет только один корень. Тогда F(a) и F(b) имеют разные знаки. Вычисляется первое приближение x₀ как полусумма крайних значений a и b. Значение x₀ делит отрезок [a, b] на две части, на одной из которых (поскольку корень единственный) функция F(x) меняет знак.

Допустим, что это отрезок [a, x₀]. Вычисляем следующее приближение как полусумму a и x₀. Приближение x₁ делит в свою очередь отрезок [a, x₀] на две части. Выбираем ту из них, на которой F(x) меняет знак и т.д. В конечном итоге получается последовательность интервалов, длина которых постепенно стягивается в точку. При этом центр интервала все более и более точно приближается к истинному значению корня.

Геометрическая интерпретация метода бисекции представлена на рис. 4.

F( x )

X ₀

X₁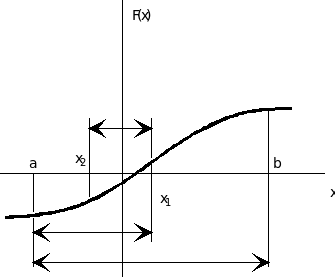

Рис.4