
- •Ен. Ф. 01 математика
- •Строительство
- •1 Решение систем линейных уравнений методами Крамера, Гаусса и обратной матрицы
- •1.1 Вопросы для самопроверки
- •2 Аналитическая геометрия на плоскости
- •Пример 2.
- •Пример 3.
- •2.1 Вопросы для самопроверки
- •3 Векторная алгебра и аналитическая геометрия в пространстве
- •Смешанным произведением трех векторов , и называется число, равное скалярному произведению вектора на вектор , т.Е.:
- •3.1 Вопросы для самопроверки
- •4 Кривые второго порядка
- •1. Окружность
- •3 Гипербола
- •Парабола
- •5 Основные теоремы о пределах
- •4.1 Вопросы для самопроверки
- •Пример варианта некоторых индивидуальных заданий на зачете
- •Задание 4. Определить вид, расположение следующих кривых второго порядка и построить их схематические графики.
- •Содержание разделов дисциплины (зачет 2 семестр)
- •Аналитическая геометрия. (1 семестр)
- •Библиографический список
Парабола
Параболой называется множество всех точек на плоскости, каждая из которых одинаково удалена от заданной точки этой же плоскости, называемой фокусом, и от заданной прямой, называемой директрисой.
Число p>0 называется параметром параболы и равно расстоянию от фокуса F до директрисы l.
Если
фокус параболы
находится в точке
![]() ,
а директриса
N
имеет уравнение
,
а директриса
N
имеет уравнение
![]() ,
то такая парабола имеет каноническое
уравнение:
,
то такая парабола имеет каноническое
уравнение:
, (18)
Точка
![]() называется вершиной параболы.
называется вершиной параболы.
Ось - ось симметрии параболы.
Расстояние
от точки
![]() параболы до фокуса F
(фокальный
радиус)
вычисляется по формуле
параболы до фокуса F
(фокальный
радиус)
вычисляется по формуле
![]() .
(19)
.
(19)
Рис.6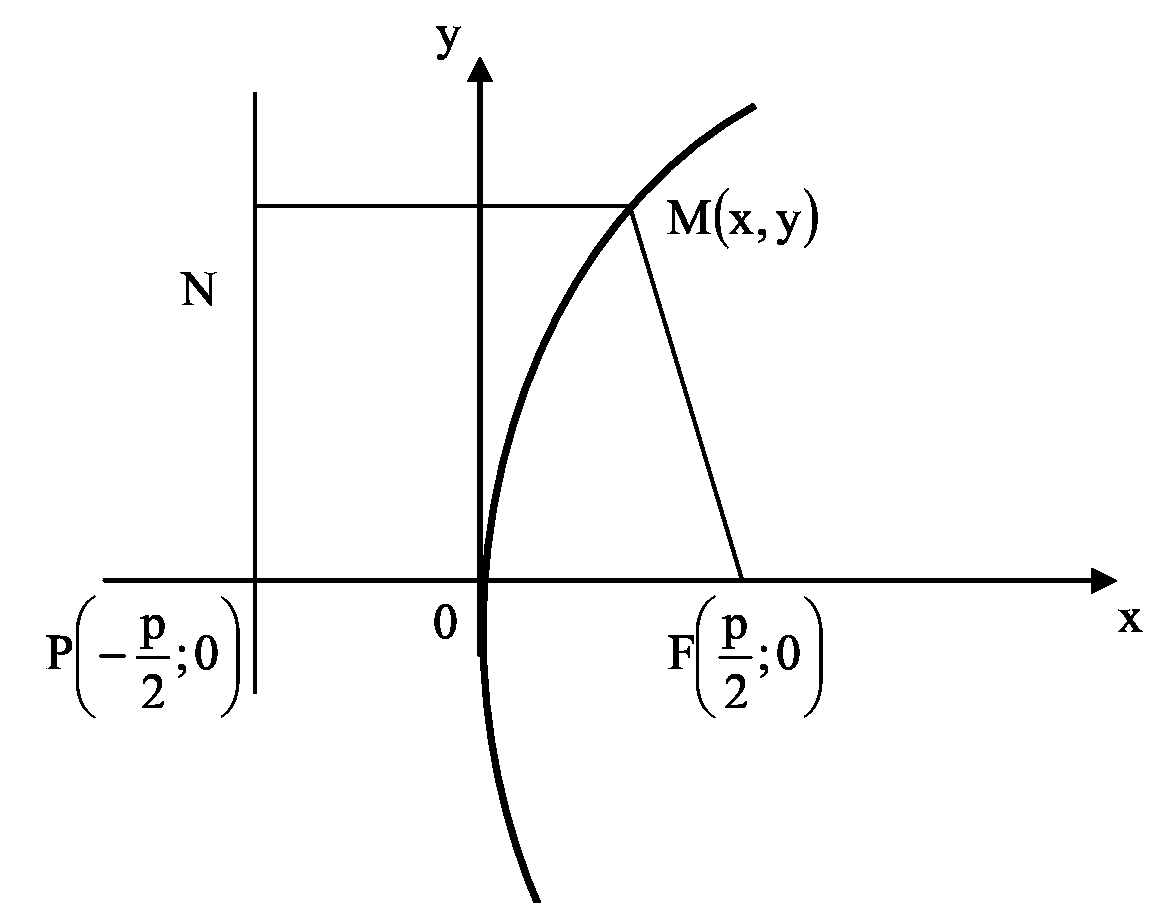
Парабола, симметричная относительно оси , с вершиной в начале координат, имеет уравнение
![]() ,
(20)
,
(20)
Фокус
параболы находится в точке
![]() .
.
Уравнение директрисы этой параболы
![]() .
(21)
.
(21)
Фокальный радиус точки параболы
![]() .
(22)
.
(22)
Графики
парабол
![]() и
и
![]() строятся в полуплоскостях, соответствующих
отрицательным значениям переменных
строятся в полуплоскостях, соответствующих
отрицательным значениям переменных
![]() и
и
![]() .
.
Пример 4.1.
Найти
уравнение параболы, симметричной
относительно оси
,
фокус которой
находится в точке пересечения прямой
![]() с осью
с осью
![]()
Решение.
Найдем
точку пересечения прямой
![]() с осью
.
с осью
.
![]()
Т.к.
расстояние от фокуса параболы до начала
координат равно
![]() ,
то
,
то
![]()
Используя
формулу (18), запишем уравнение параболы:
![]() .
.
Задачи для самостоятельного решения:
Составить уравнение параболы, вершина которой находится в начале координат, зная, что:
парабола расположена в правой полуплоскости симметрично относительно оси и ее параметр
 ;
;парабола расположена в левой полуплоскости симметрично относительно оси и ее параметр
 ;
;парабола расположена в верхней полуплоскости симметрично относительно оси и ее параметр
 ;
;парабола расположена в нижней полуплоскости симметрично относительно оси и ее параметр
 .
.
Определить величину параметра и расположение относительно координатных осей следующих парабол: 1)
 ;
2)
;
2)
 ;
3)
;
3)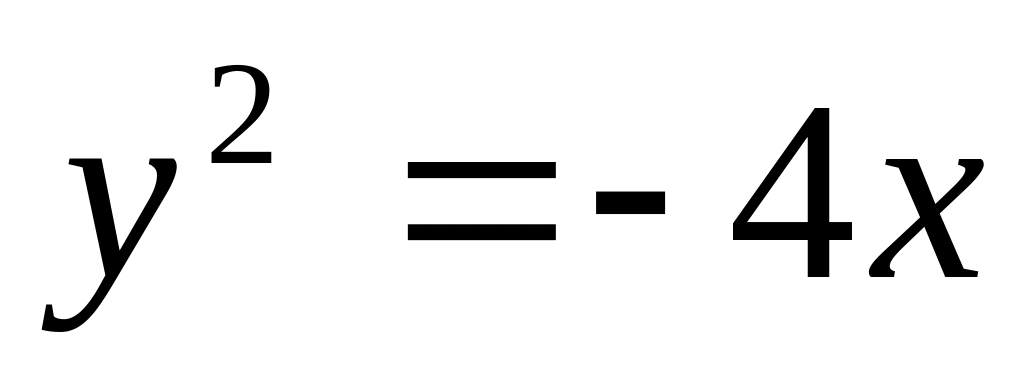 ;
4)
;
4)
 .
.Составить уравнение параболы, вершина которой находится в начале координат, зная, что:
парабола расположена симметрично относительно оси и проходит через точку
 ;
;парабола расположена симметрично относительно оси и проходит через точку
 ;
;парабола расположена симметрично относительно оси и проходит через точку
 ;
;парабола расположена симметрично относительно оси и проходит через точку
 .
.
4. Установить, какие линии определяются следующими уравнениями:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() .
Изобразить эти линии на чертеже.
.
Изобразить эти линии на чертеже.
5.
Найти фокус
![]() и уравнение директрисы параболы
и уравнение директрисы параболы
![]() .
.
6.
Вычислить фокальный радиус точки
параболы
![]() ,
если абсцисса точки
равна 7.
,
если абсцисса точки
равна 7.
7.
Вычислить фокальный радиус точки
параболы
![]() ,
если ордината точки
равна 6.
,
если ордината точки
равна 6.
8.
На параболе
![]() найти точки, фокальный радиус которых
равен 13.
найти точки, фокальный радиус которых
равен 13.
9.
Составить уравнение параболы, если дан
фокус
![]() и уравнение директрисы
и уравнение директрисы
![]() .
.
10.
На параболе
![]() найти точку, расстояние которой от
директрисы параболы равно 4.
найти точку, расстояние которой от
директрисы параболы равно 4.
11.
Составить уравнение параболы с вершиной
в начале координат, симметричной
относительно оси
![]() и отсекающей на прямой
и отсекающей на прямой
![]() хорду длиной
хорду длиной
![]() .
.
12.
На параболе
![]() найти точку, расстояние которой от
прямой
найти точку, расстояние которой от
прямой
![]() равно 2.
равно 2.
Уравнения кривых второго порядка с осями симметрии, параллельными осям координат. Приведение общего уравнения кривой второго порядка, не содержащего члена с произведением текущих координат,
к каноническому виду
Даны
две прямоугольные системы координат
![]() и
и
![]() со свойствами: оси
и
со свойствами: оси
и
![]() ,
а также
и
,
а также
и
![]() параллельны и одинаково направлены, а
начало
параллельны и одинаково направлены, а
начало
![]() системы
имеет известные координаты
системы
имеет известные координаты
![]() относительно системы
.
относительно системы
.
Тогда
координаты
![]() и
и
![]() произвольной точки
плоскости связаны соотношениями:
произвольной точки
плоскости связаны соотношениями:
![]()
![]() (23)
(23)
Формулы (18) называются формулами преобразования координат при параллельном переносе осей координат.
Уравнение
эллипса с полуосями
и
,
центром в точке
![]() и осями симметрии, параллельными
координатным осям, имеет вид:
и осями симметрии, параллельными
координатным осям, имеет вид:
![]() ,
(24)
,
(24)

Рис.7
Уравнение гиперболы с осями, параллельными координатным, имеет вид:
![]() ,
(25)
,
(25)
где
![]() -
координаты центра гиперболы.
-
координаты центра гиперболы.
Уравнение параболы с осью симметрии, параллельной оси абсцисс, имеет вид:
![]() ,
(26)
,
(26)
![]() ,
(27)
,
(27)
Если ось параболы параллельна оси ординат, то
![]() ,
(28)
,
(28)
![]() ,
(29)
,
(29)
Пример 5.1.
Уравнение
линии
![]() привести к каноническому виду и построить
ее.
привести к каноническому виду и построить
ее.
Решение.
Выделим в правой части уравнения полные квадраты:

Уравнение
определяет гиперболу с центром в точке
![]() ,
действительной полуосью
,
действительной полуосью
![]() и мнимой полуосью
и мнимой полуосью
![]() .
Прямые
.
Прямые
![]() и
и
![]() являются осями симметрии гиперболы,
параллельными координатным осям
и
соответственно.
являются осями симметрии гиперболы,
параллельными координатным осям
и
соответственно.
Построим
основной прямоугольник гиперболы со
сторонами
![]() и
и
![]() с центром в точке
(рис. 8). Диагонали этого прямоугольника
являются асимптотами гиперболы.
с центром в точке
(рис. 8). Диагонали этого прямоугольника
являются асимптотами гиперболы.
Рис.8
Найдем
уравнения асимптот. Так как асимптоты
проходят через точку
и имеют угловые коэффициенты
![]() (см. уравнение (12)), то уравнения прямых
запишутся следующим образом:
(см. уравнение (12)), то уравнения прямых
запишутся следующим образом:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Получим
уравнения асимптот:
![]() и
и
![]() .
.
Найдем
вершины гиперболы. В системе координат
:
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() .
Из формул (23) получим:
.
Из формул (23) получим:
Точка
:
![]() Точка
:
Точка
:
![]()
Итак,
в системе координат
вершины гиперболы выглядят следующим
образом:
![]() ,
,
![]() .
.
Найдем
фокусы гиперболы. Из формулы (10) имеем:
![]() ;
;
![]() .
Координаты фокусов в системе координат
:
и
.
Координаты фокусов в системе координат
:
и
![]() .
.
Точка
![]() :
:
![]() Точка
Точка
![]() :
:
![]()
В
системе координат
координаты фокусов:
![]() ,
,
![]()
По
формуле (11) вычислим эксцентриситет:
![]()
Задачи для самостоятельного решения:
Каждое из следующих уравнений путем параллельного переноса привести к каноническому виду; определить тип; изобразить на чертеже расположение геометрических образов относительно старых и новых координат. Определить основные характеристики.
1.
![]() 9.
9.
![]()
2.
![]() 10.
10.
![]()
3.
![]() 11.
11.
![]()
4.
![]() 12.
12.
![]()
5.
![]() 13.
13.
![]()
6.
![]() 14.
14.
![]()
7.
![]() 15.
15.
![]()
8.
![]() 16.
16.
![]()
