- •Исходные данные
- •1. Структурный анализ механизма
- •1.1 Назначение механизма
- •1.2 Звенья механизма
- •1.3 Кинематические пары
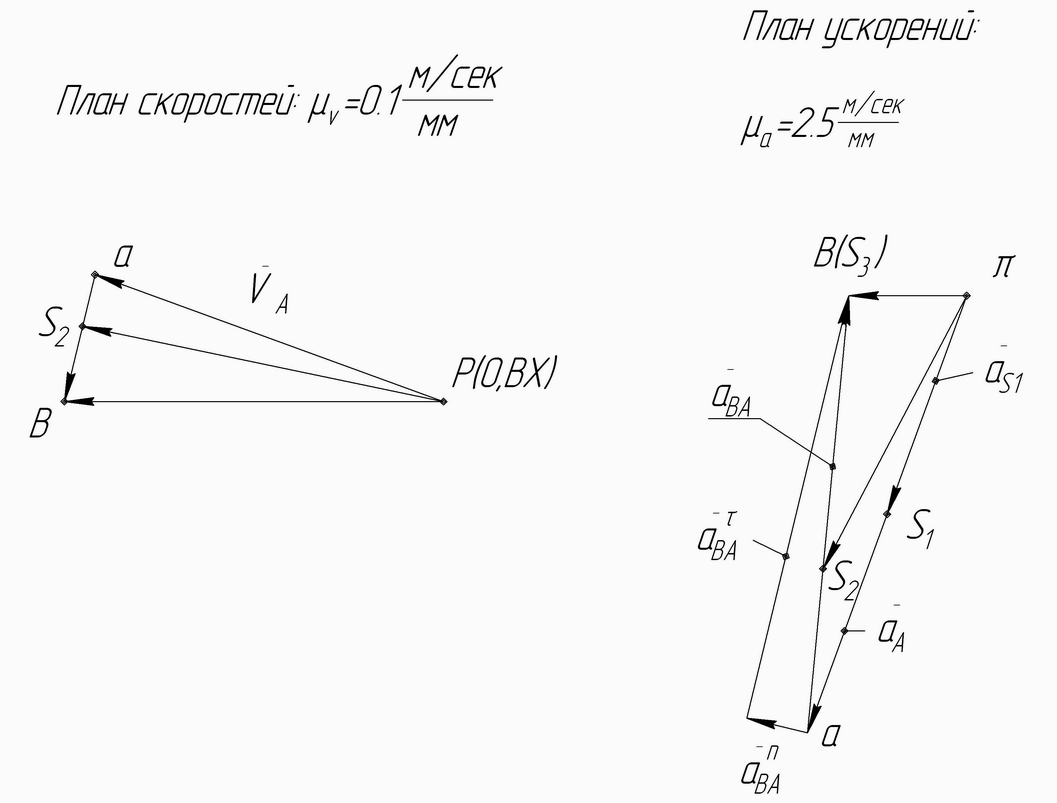
- •2. Построение планов скоростей и ускорений
- •3. Силовой расчет механизма
- •Литература
- •Задания для расчетно-графической работы
- •Содержание
- •Расчет кривошипно–ползунного механизма
- •625000, Г.Тюмень, ул.Володарского, 38
- •625039, Г.Тюмень, ул. Киевская, 52
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ ТРАНСПОРТА
Кафедра Детали машин
РАСЧЕТ КРИВОШИПНО–ПОЛЗУННОГО МЕХАНИЗМА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к расчетно-графической работе по Теории механизмов и машин для студентов специальностей НР-130503, ПСТ-130501, НБ-130504, МОП-130602, АТХ-190601, СТЭ-190603, ПДМ-190205, СП-150202, ПТИ-260703, ТМ-151001, МКC-151002, МХП-240801, МСО-190207
очной и заочной полной и сокращенной форм обучения
Тюмень 2007
Утверждено редакционно-издательским советом
Тюменского государственного нефтегазового университета
Составители: профессор, к.т.н. Кривохижа Василий Николаевич
ассистент, Панков Дмитрий Николаевич
© государственное образовательное учреждение высшего профессионального образования
«Тюменский государственный нефтегазовый университет»
2007 г
Исходные данные
Для заданного положения кривошипно–ползунного механизма (рис.1) необходимо:
Произвести структурный анализ механизма;
Построить план скоростей, план ускорений;
Выполнить силовой расчет механизма.
Дано:
Размеры:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
Число
оборотов кривошипа постоянно и равно
![]() ;
;
![]() ;
;
![]() ;
;
Массы звеньев:
![]() ,
,
![]() ,
,
![]() .
.
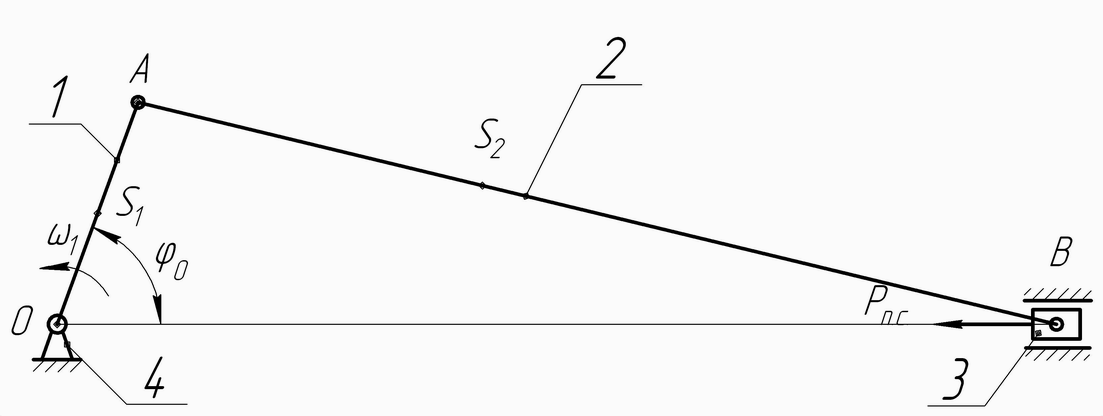
Рис.
1 Кривошипно-ползунный
механизм
1. Структурный анализ механизма
1.1 Назначение механизма
Преобразовать вращательное движение кривошипа в поступательное движение ползуна
1.2 Звенья механизма
Номер звена |
Наименование |
Подвижность |
Число подвижных звеньев |
1 |
Кривошип |
Подвижное |
3 |
2 |
Шатун |
Подвижное |
|
3 |
Ползун |
Подвижное |
|
4 |
Стойка |
Неподвижное |
1.3 Кинематические пары
Обозначение |
Соединяемые элементы |
Тип пары |
Индекс пары |
Число пар |
|||
Вид движения |
Характер соединения |
Подвижность |
Одно подвижных |
Двух подвижных |
|||
О |
1,4 |
Вращательное |
Низшая |
Одноподвижная |
В(1,4) |
|
|
А |
1,2 |
Вращательное |
Низшая |
Одноподвижная |
В(1,2) |
||
В |
2,3 |
Вращательное |
Низшая |
Одноподвижная |
В(2,3) |
||
В |
3,4 |
Поступательное |
Низшая |
Одноподвижная |
П(3,4) |
||
1.4 Определение степени подвижности механизма
![]()
Лишних и пассивных связей нет.
1.5 Расчленяем механизм на группы Ассура
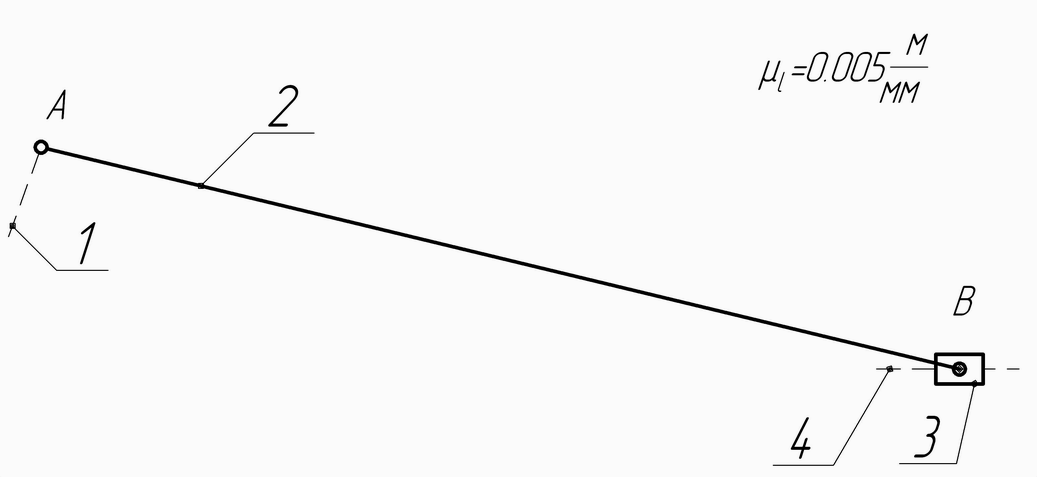
Группа
Ассура
![]() класса, 2–го порядка, 2–го вида;
класса, 2–го порядка, 2–го вида;
![]() ;
;
![]() ;
;
![]() .
.
Структурная формула:
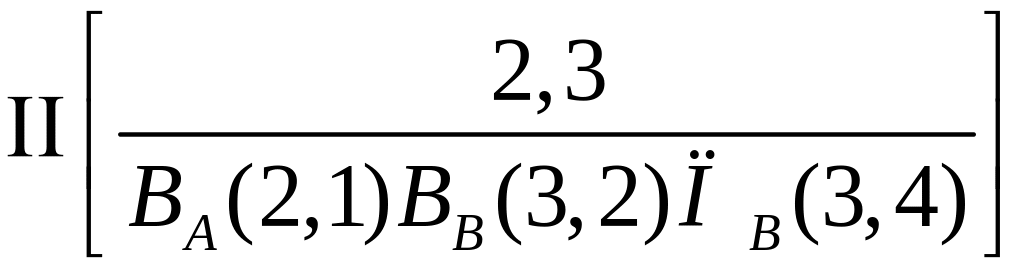 .
.
Начальный механизм
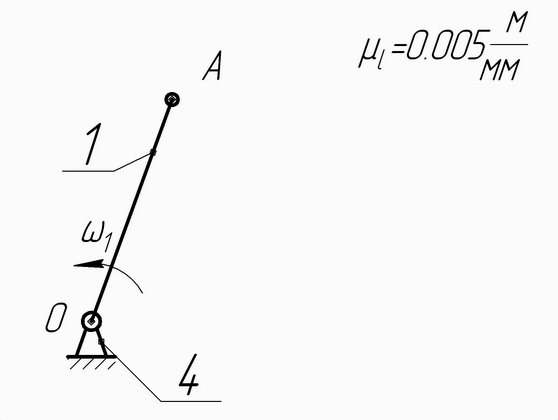
І класса
;
![]() ;
;
![]() .
.
1.7 Структурная формула начального механизма:
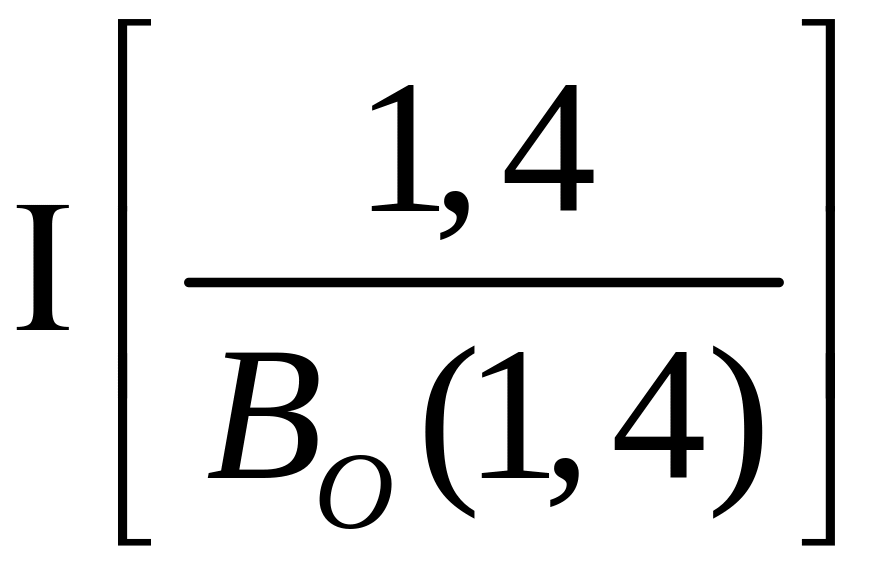
Структурная формула кривошипно-ползунного механизма:
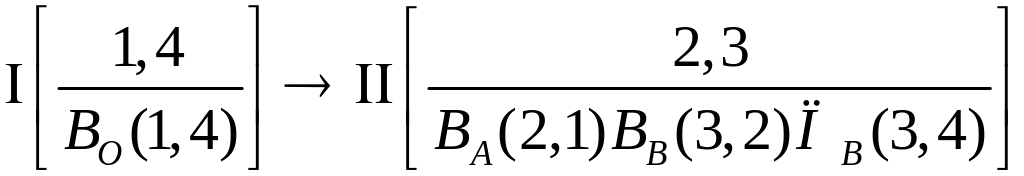 .
.
1.8
Кривошипно-ползунный механизм
![]() класса
класса
2. Построение планов скоростей и ускорений
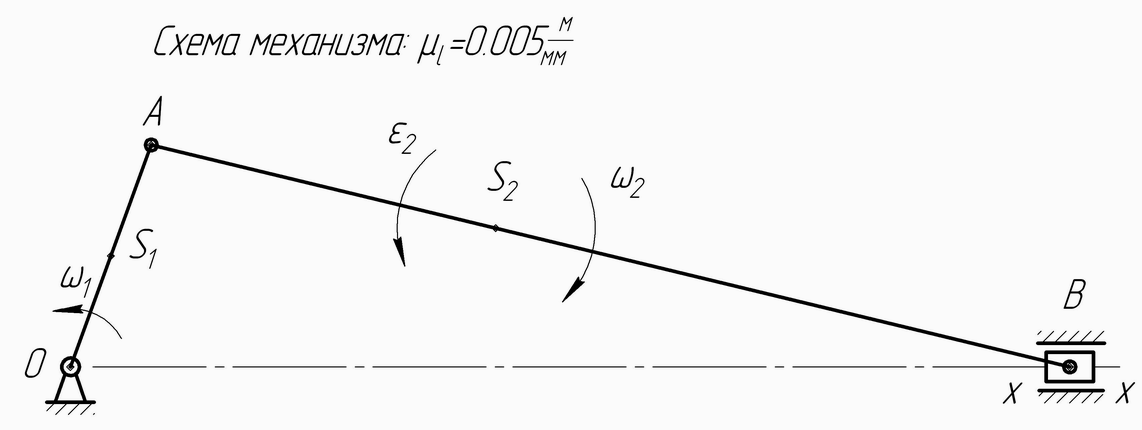
а)
б) |
в) |
Рис. 2 К построению планов скоростей и ускорений
Определяем угловую скорость кривошипа
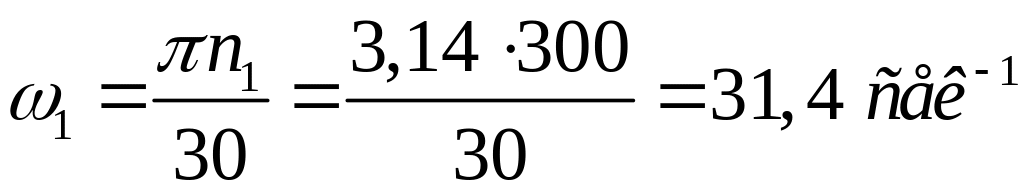
Определяем скорость точки A
![]()
Вектор
скорости точки A
–
![]() направлен перпендикулярно кривошипу
OA
в сторону вращения.
направлен перпендикулярно кривошипу
OA
в сторону вращения.
Задаемся
коэффициентом масштаба плана скоростей
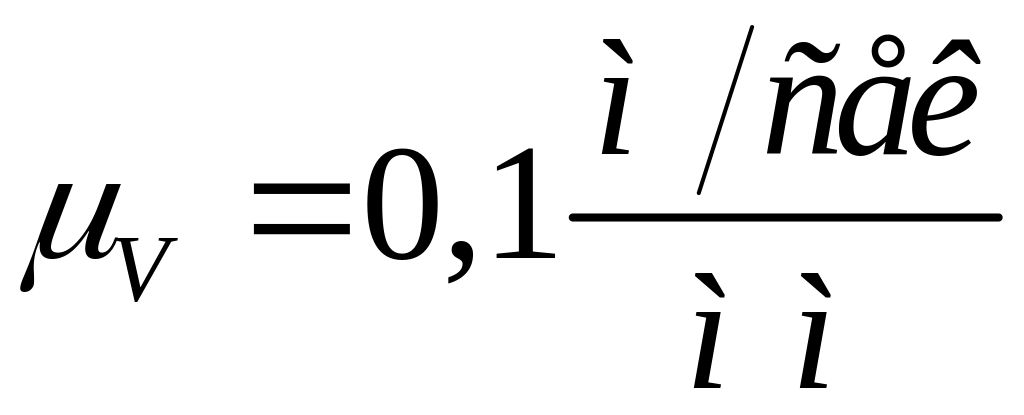 и вычисляем величину отрезка
и вычисляем величину отрезка
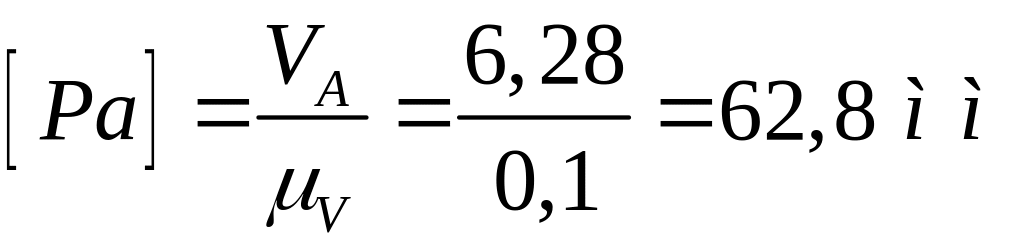
Откладываем этот отрезок в указанном направлении (рис 2,б).
Составляем векторное уравнение для определения скорости точки B группы Ассура (2,3):
![]() (1)
(1)
В
уравнении (1) вектор
полностью известен и по величине и по
направлению (отрезок
![]() ,
изображающий этот вектор, уже отложен).
Вектор
,
изображающий этот вектор, уже отложен).
Вектор
![]() направлен перпендикулярно звену AB,
а вектор
направлен перпендикулярно звену AB,
а вектор
![]() – по направляющей xx.
Величины этих векторов неизвестны.
– по направляющей xx.
Величины этих векторов неизвестны.
Согласно
векторному уравнению, через конец
вектора
(через
точку
a)
проводим направление вектора
,
а через начало вектора
(через полюс P)
– направление вектора
.
Точку пересечения указанных направлений
обозначим b.
Тогда отрезки
![]() и
и
![]() в выбранном масштабе будут соответствовать
скоростям
и
.
в выбранном масштабе будут соответствовать
скоростям
и
.
Измеряем эти отрезки по плану скоростей:
![]() ,
,
![]() ;
;
вычисляем соответствующие скорости:
![]() ;
;![]() .
.
Скорость точки S2 определяем по теореме подобия
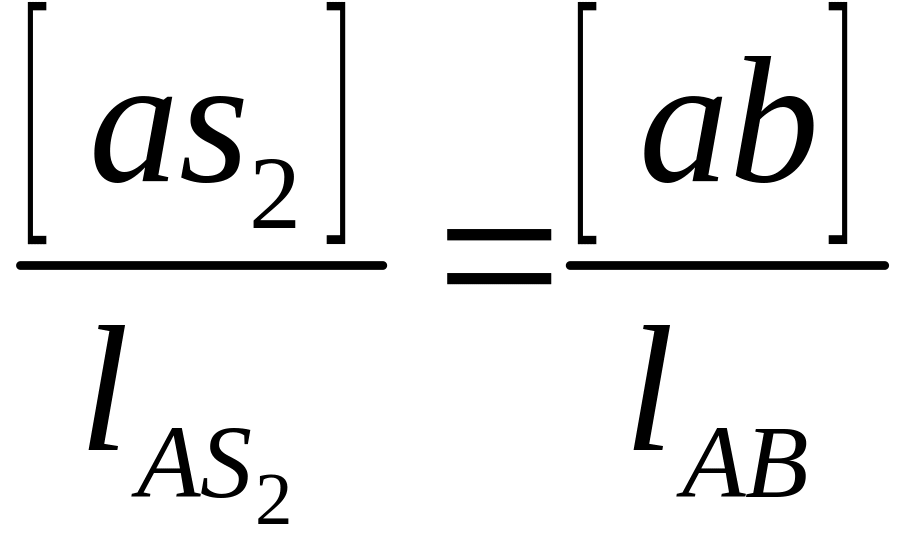 ,
,
откуда
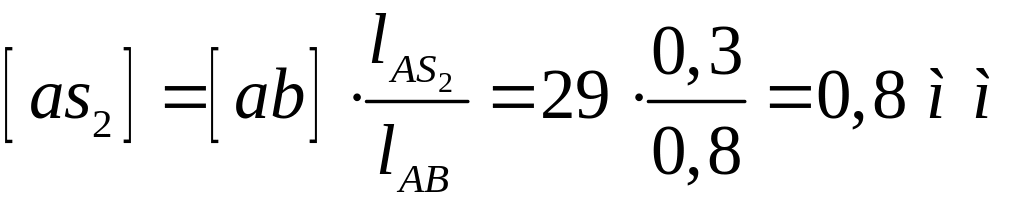 ,
,
где s2 – точка на плане скоростей, соответствующая точке S2 механизма.
Откладывая
отрезок
![]() на плане скоростей, вдоль отрезка
,
получим точку s2.
Соединяя эту точку с полюсом, получим
отрезок
на плане скоростей, вдоль отрезка
,
получим точку s2.
Соединяя эту точку с полюсом, получим
отрезок
![]() изображающий в масштабе вектор
изображающий в масштабе вектор
![]() .
Измеряем величину этого отрезка.
.
Измеряем величину этого отрезка.
![]()
и вычисляем скорость
![]()
Определяем угловую скорость шатуна
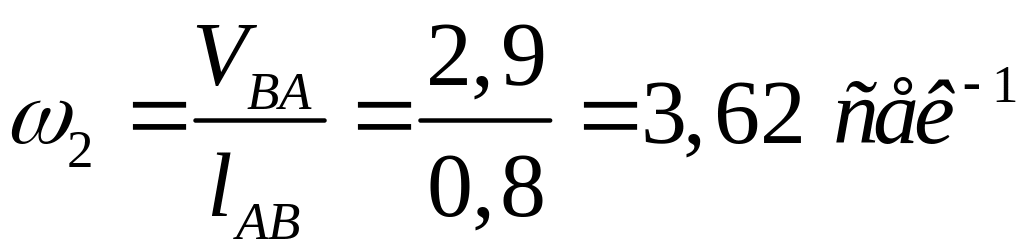 .
.
Для
определения направления угловой скорости
![]() следует вектор
перенести в точку B
механизма и посмотреть, как она в
соответствии с направлением этого
вектора движется относительно точки
А.
В нашем случае
направлена по часовой стрелке.
следует вектор
перенести в точку B
механизма и посмотреть, как она в
соответствии с направлением этого
вектора движется относительно точки
А.
В нашем случае
направлена по часовой стрелке.
Определим ускорение точки А. Так как угловая скорость кривошипа постоянна, то полное ускорение точки А равно ее нормальному ускорению.
![]() .
.
Вектор
![]() – направлен по кривошипу OA
от точки O
к точке A
(к центру вращения кривошипа).
– направлен по кривошипу OA
от точки O
к точке A
(к центру вращения кривошипа).
Задаваясь
коэффициентом масштаба плана ускорений
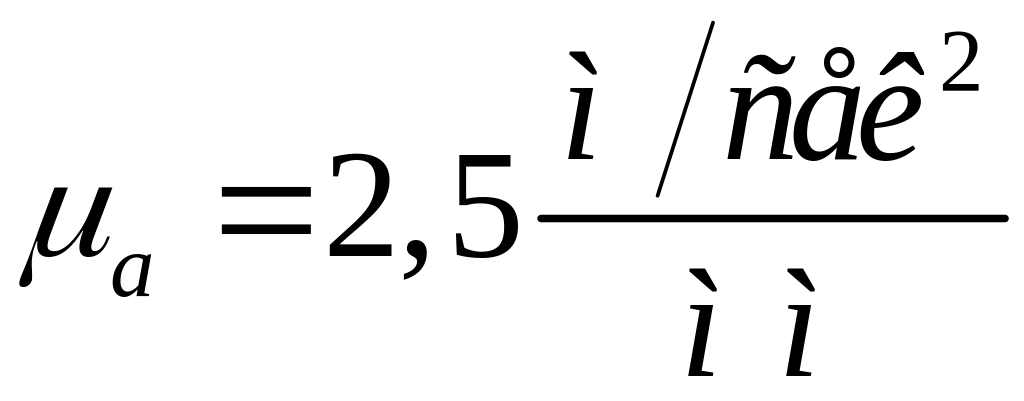 ,
определяем величину отрезка
,
определяем величину отрезка
![]() ,
изображающего вектор
на плане ускорений:
,
изображающего вектор
на плане ускорений:
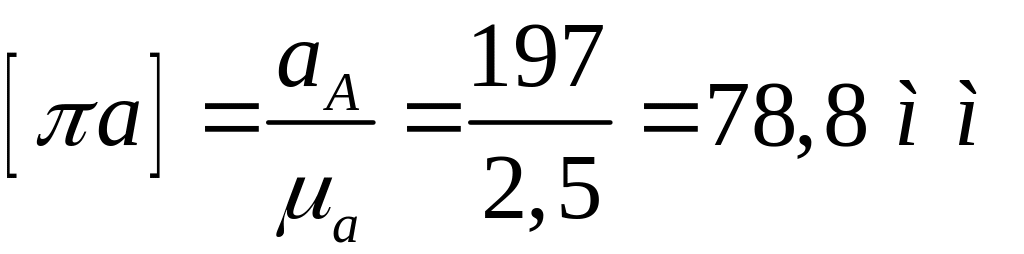
Откладываем этот отрезок в указанном направлении (рис.2,в).
Составляем векторное уравнение для определения ускорения точки B группы Ассура (2,3):
![]() (2)
(2)
Разложим
ускорение
![]() на составляющие
на составляющие
![]() ,
(3)
,
(3)
тогда
![]() (4)
(4)
В
уравнении (4) вектор
уже полностью известен, а величина
вектора
![]() вычисляется по формуле
вычисляется по формуле
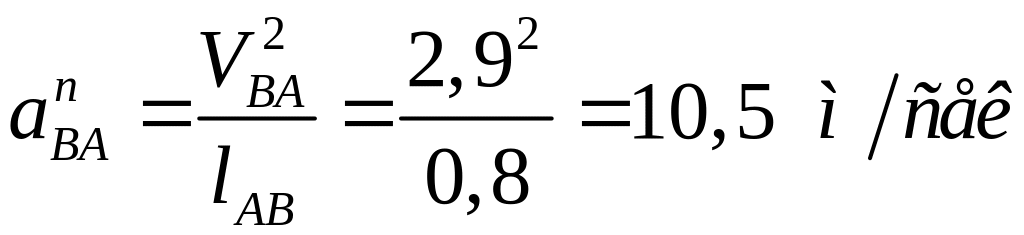 .
.
Определим
величину отрезка
![]() ,
изображающего вектор
на плане
,
изображающего вектор
на плане
![]() ускорений,
ускорений,
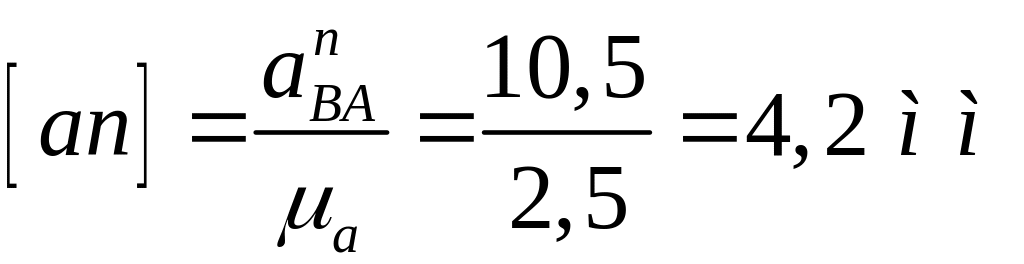 .
.
Векторы
в уравнении (4) направлены следующим
образом:
![]() ,
,
![]() (направлен от точки B
к точке A),
(направлен от точки B
к точке A),
![]() .
.
В
соответствии с правой частью векторного
уравнения к вектору
прикладываем вектор
(т.е. от точки a
откладываем в указанном направлении
отрезок
),
а через конец вектора (через точку n)
проводим направление вектора
![]() .
В соответствии с левой частью уравнения
через полюс
.
В соответствии с левой частью уравнения
через полюс
![]() проводим направление вектора
проводим направление вектора
![]() .
Точку пересечения указанных направлений
обозначим буквой b.
Таким образом, отрезки
.
Точку пересечения указанных направлений
обозначим буквой b.
Таким образом, отрезки
![]() и
и
![]() изображают в масштабе соответственно
ускорения
и
.
Измеряем величины этих отрезков:
изображают в масштабе соответственно
ускорения
и
.
Измеряем величины этих отрезков:
![]() ,
,
![]() .
.
вычисляем ускорения:
![]()
![]()
Соединяя точки a и b, получим отрезок , который в соответствии с уравнением (3) изображает вектор полного относительного ускорения . Измеряем величину отрезка
![]()
и вычисляем ускорение
![]()
Определяем ускорение точки S2. По теореме подобия имеем:
,
откуда

Откладывая
этот отрезок вдоль отрезка
,
получим точку s2.
Соединяя ее с полюсом
,
получим отрезок
![]() ,
изображающий вектор
,
изображающий вектор
![]() .
Измеряем этот отрезок
.
Измеряем этот отрезок
![]()
и вычисляем ускорение
![]() .
.
По аналогии
![]()
Находим величину углового ускорения шатуна
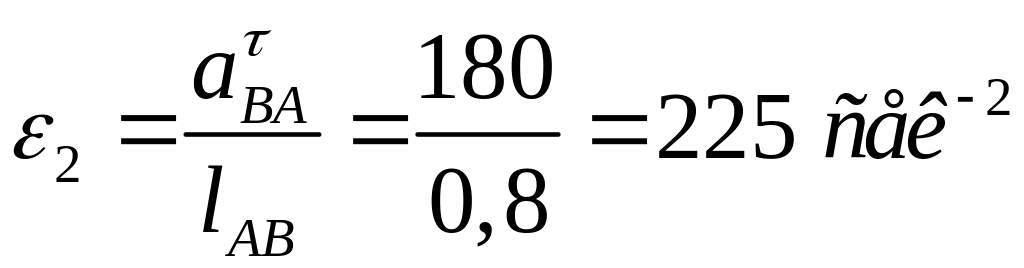
Для
определения направления
![]() следует вектор
перенести в точку B
механизма и посмотреть, как она в
соответствии с этим вектором движется
относительно точки A.
В нашем случае
направлено против часовой стрелки.
следует вектор
перенести в точку B
механизма и посмотреть, как она в
соответствии с этим вектором движется
относительно точки A.
В нашем случае
направлено против часовой стрелки.