Лабораторная работа № 2

РАЗМЕЩЕНИЕ КОНСТРУКТИВНЫХ ЭЛЕМЕНТОВ В МОНТАЖНОМ

ПРОСТРАНСТВЕ

1. Цель работы

Целью настоящей работы является изучение задачи размещения конструктивных элементов в монтажном пространстве, а также исследование некоторых возможных алгоритмов ее решения.

2. Теоретическая часть

2.1. Введение

Под задачей размещения в теории конструирования понимается задача определения такого местоположения элементов в заданном монтажном пространстве, при котором наилучшим образом удовлетворяются некоторые требования.

В качестве элемента здесь могут выступать радиодетали, микросхемы, ячейки, панели, блоки, а в качестве монтажного пространства ячейки, панели, блоки, шкафы. При этом предполагается, что элементы в монтажном пространстве определенным образом соединяются между собой. Эти соединения могут быть выполнены посредством навесных или печатных проводников, жгутовых соединений или других информационных магистралей.

Задача размещения носит в общем случае многоцелевой характер и при ее решении должна производиться оптимизация по совокупности критериев качества [2]. Однако в каждом конкретном случае обычно удается выделить наиболее важный критерии, учитывая другие показатели в качестве ограничений задачи. Известные в литературе алгоритмы размещения оптимизируют в основном следующие показатели качества [I]:

а) суммарную длину всех соединении;

б) длину самой длинной связи;

в) число связей между модулями, находящимися в соседних позициях;

г) число пересечений проводников;

д) число цепей о возможно более простой конфигурацией. Существующие алгоритмы, решения задачи размещения можно разделить на следующие группы:

• итерационные алгоритмы, использующие перестановки элементов;

• конструктивные алгоритмы последовательного и параллельно-последовательного типов;

• непрерывно-дискретные алгоритмы, основанные на силовых моделях;

• использующие комбинаторные методы.

В настоящей лабораторной работе исследуются два приближенных алгоритма размещения применительно к задаче установки модулей на плате.

2.2. Постановка задачи

Имеется плоская или объемная плата с узлами, предназначенными для установки модулей. Задана матрица расстояний между, отдельными узлами платы, включая и расстояние между узлами и контактами платы:

(1)

Элементы S_ij матрицы S определяются либо соотношениями вида:

(2)

либо

(3)

где x_ij и x_j, y_j - координаты i-го и j-го узла соответственно.

Даны некоторая совокупность модулей, подлежащих размещению на плате, и матрица числа связей этих модулей между собой, а также между модулями и контактами.

(4)

Без ограничения общности будем далее считать, что n =m, так как в случае m<n можно всегда ввести фиктивные модули с элементами при в матрице связей ρ.

Необходимо найти размещение модулей на плате с минимальной суммарной длиной всех соединений.

2.3. Алгоритм парных перестановок

Суть этого итерационного алгоритма заключается в последовательном, целенаправленном улучшении произвольного начального размещения модулей на плате по выбранному критерию путем парных перестановок. С этой целью на каждой итерации алгоритма производится вычисление приращений суммарной длины всех связей для всевозможных парных перестановок модулей. Из всего множества перестановок, дающих отрицательные приращения, выбирается подмножество, которое удовлетворяет следующим требованиям:

1. выбранное подмножество перестановок позволяет максимально уменьшить суммарную длину всех связей;

2. подмножество образует лишь независимые перестановки, т.е. такие парные перестановки, в которые входят модули, не связанные с модулями других переставляющихся пар.

Далее осуществляются перестановки выделенных таким образом пар модулей и. переход к следующей итерации.

Описанный итерационный процесс сходится к локально-оптимальному размещению модулей на плате.

Выведем формулы для суммарной длины L всех связей и ее приращения ΔL при перемещении модулей.

Пусть на некоторой итерации имеется следующее размещение модулей на плате :

узлы	1	2	3	…	l	…	n
модули	t1	t2	t3	…	tl	…	tn

где t_l – номер модуля, оказавшегося размещенным в l-м узле платы

Поставим в соответствие этому размещению матрицу ,

где - элементы матрицы (4), находящиеся на пересечении строки t_i и столбца t_j ,r_ij= . Определенный таким образом элемент r_ij матрицы R равен числу связей между модулями t_i и t_j, находящимися на данной итерации в узлах i и j соответственно.

Поскольку расстояние между узлами i и к равно S_ik, то суммарная длина связей между модулями t_i и t_k

L_ik=r_ikS_ik.

Отсюда суммарная длина связей t_i -го модуля, расположенного в i-м узле, со всеми модулями совокупности равна:

,

И для суммарной длины всех связей при данном размещении получаем

(5)

Найдем теперь формулу для приращения суммарной длины всех связей при перестановке модулей t_i и t_j, расположенных в узлах i и j соответственно.

Для суммарной длины связей t_i-го и t_j-го модулей со вcеми остальными модулями имеем выражение:

, (6)

где последнее слагаемое соответствует длине связей между модулями, расположенными в i-й и j-й позициях.

При взаимной перестановке модулей о номерами t_i и t_j суммарная длина их связей со. всеми остальными модулями

. (7)

Заметим, что взаимная перестановка модулей с номерами t_i и t_j соответствует перестановке строк и столбцов с номерами- i и j в матрице R формула же (7) получена лишь путем перестановки i-го и j-го столбцов матрицы R. Именно поэтому в ней отсутствует слагаемое вида .

Вычитая из (7) выражение (6), определяем приращение суммарной длины всех связей после перестановки модулей с номерами t_i и t_j.

(8)

По этой формуле принципиально могут быть вычислены элементы матрицы приращений для всевозможных парных перестановок. Однако более удобно использовать для вычисления элементов матрицы приращений некоторые вспомогательные построения.

Введем в рассмотрение матрицу Р с помощью следующего выражения:

(9)

Нетрудно видеть, что полусумма диагональных членов матрицы Р (полуслед) равна суммарной длине всех связей, определяемой формулой (5). С помощью элементов матрицы Р могут быть также легко вычислены и элементы ΔL_ij матрицы приращений для всевозможных парных перестановок.

Действительно, о учетом симметричность матрицы S выражение (8) преобразуется к виду:

(10)

где

q_ij =P_ij.=P_ii+P_ji-P_jj (11)

Вычисляя по формулам (10), (11) элементы матрицы приращений , можно выбрать подмножество перестановок, удовлетворяющих перечисленным выше требованиям.

Пример. Пусть начальное размещение связанной системы модулей на плате с 6 узлами имеет вид, представленный на рис. 1.а. При этом нумерация элементов в начальном размещении совпадает о нумерацией узлов, а во втором узле размещен разъем, который запрещено переносить на другую позицию.

а) б)

Рис.1

Если расстояние S_ij между узлами i и j платы определено по формуле (2), то матрица расстояний S имеет вид:

(12)

Составим соответствующие начальному размещению матрицы R и P=RS.

(13)

Суммарная длина всех связей в начальном размещении равна полуследу матрицы Р, т.е.

.

Вычисляем далее последовательно матрицы :

.

В матрице ΔL прочерком (-) указаны элементы, которые заведомо являются положительными в силу положительности соответствующих элементов матрицу q, а также элементы, отвечающие недопустимому переразмещению разъема (модуля 2).

Из рассмотрения матрацы ΔL видно, что к уменьшению суммарной длины всех связей приводят взаимные перестановки пар модулей, расположенных в начальном размещении в следующих узлах:

3 и 4 (ΔL=-11), 3 и 6 (ΔL=-2), 5 и 6 (ΔL=-7).

Упорядочивая эти пары по возрастанию оценки и проверяя по матрице связей R условия независимости, приходим к выводу, что допустимой является лишь одна перестановка-(пара 3 и 4).

Производим переразмещение модулей (рис.1,б) и приводим в соответствие новому размещению матрицы R и Р. С этой целью необходимо в матрице R, соответствующей начальному размещению, поменять местами элементы 3-го и 4-го столбцов и 3-й и 4-й строк. Матрица Р получается умножением новой матрицы R на матрицу S (12). Тогда

Суммарная длина всех связей нового размещения

Выполняем следующую итерацию:

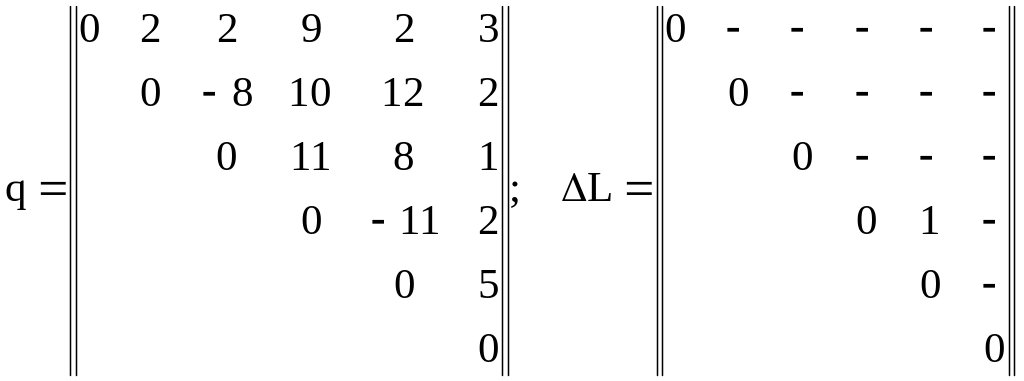
Матрица ΔL не имеет ни одного отрицательного элемента. Поэтому процесс улучшения начального размещения закончен. Таким образом, размещение, изображенное на рас. 1.б, соответствует локальному оптимуму.

2.4. Последовательный алгоритм размещения

Сущность этого конструктивного алгоритма сводится к последовательному (на каждом шаге) размещению очередного модуля в определенный узел платы. Предполагается, что часть модулей или хотя бы один заранее размещены на монтажной плоскости. В качестве таких модулей могут быть выбраны либо контакты разъема, либо модули, фиксируемые на определенных позициях в соответствии с директивными указаниями разработчиков. При выборе очередного модуля оптимизируется целевая акция, учитывающая связи этого модуля с множествами ранее размещенных и неразмещенных модулей, в качестве такой (функции может быть, например, выбрана следующая:

, (14)

где и соответственно множество размещенных и множество неразмещенных на К- м шаге алгоритма модулей, ρ_ij - элемент матрицы связей (4).

Тогда задача сводится к максимизации этого выражения по всем .

Далее для выбранного модуля находится наиболее приемлемая позиция на плате. Для выбора такой позиции используется критерий минимальности длины связей размещаемого модуля с уже размещенными модулями. При этом, очевидно, нет необходимости рассматривать все не занятые на этом шаге позиции, а достаточно оценить лишь множество позиций, соседних с занятыми. Поэтому позиция ρ_i, в которую необходимо поместить выбранный i-й модуль, определяется из условия минимизации следующего выражения:

где Г^к- множество позиций, соседних с занятыми; P_j позиция, в которой размещен j-й модуль; - элемент матрицы (I).

Описанный последовательный алгоритм наиболее прост в реализации, дает малое время решения задачи и не требует начального размещения. Этот алгоритм может использоваться как самостоятельно, так и в комбинированных алгоритмах в качестве начального этапа для получения исходного размещения.

3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

3.1. Расчетная часть

3.1.1. Для полученного варианта принципиальной схемы устройства составить графовую модель, используемую для последующего решения задачи размещения.

2. Провести решение задачи "вручную" для полученного варианта задания с помощью последовательного алгоритма. Представить графически результаты решения. Подсчитать суммарную длину межсоединений.

3. Составить исходные данные в форматах, указанных преподавателем, для трех случаев:

а) последовательного алгоритма;

б) алгоритма парных перестановок с произвольным начальным размещением;

в) алгоритма парных перестановок с начальным размещением, являющимся результатом размещения с помощью последовательного алгоритма.

3.2. Экспериментальная часть

1. Подготовить ЭВМ к работе.

1. Вызвав программу последовательного алгоритма размещения в режиме диалога ввести запрашиваемые ЭВМ исходные данные.

3.2.3. Получить распечатку с результатами машинного решения.

3.2.4. Выполнить п.п. 3.2.2, 3.2.3 для алгоритма парных перестановок для двух вариантов начального размещения (произвольного и являющегося результатом размещения с помощью последовательного алгоритма).

4. СОДЕРЖАНИЕ ОТЧЁТА ПО РАБОТЕ

1. Исходное задание на исследование.

2. Результаты, полученные в п. 3.1.2.

3. Исходные данные для машинного размещения по п. 3.1.3.

4. Представленное графически результаты размещения, полученные в п.п.. 3.1.2, 3.2.2, 3.2.4.

Графики изменения суммарной длины связей в зависимости от номера итерации, построенные по результатам.

6. Анализ полученных результатов.

7. Выводы по работе.

5. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Как формулируется задача размещения в конструировании?

2. В чем суть последовательного алгоритма размещения?

1. Выведите формулу для приращения суммарной длины связей при перестановке двух модулей.

4. Почему полуслед матрицы Р равен суммарной длине всех связей?

5. Какие пары модулей переставляются на одной итерации алгоритма парных перестановок?

Библиографический список

1. Селютив В.А, Машинное конструирование электронных устройств. М.: Сов. радио, 1977. 381 с.

2. Гавриленко В.И., Юсим Г.В. Теоретические основы конструирования и надежности электронно-вычислительной аппаратуры. Рязань:РРТИ, 1976. 208с.