Приклад:

Розглянемо показники обсягу викидів шкідливих речовин в атмосферне повітря по районах Житомирської області за 2005 рік.

Побудуємо ряд розподілу районів за обсягом викидів шкідливих речовин, виділивши п'ять груп з нерівними інтервалами (табл. 2.4.3.):

I група - обсяг викидів до 0,6 тис. т;

II група - обсяг викидів від 0,6 до 1,2 тис. т;

3. група - обсяг викидів від 1,2 до 2,4 тис. т;

3. Група- обсяг викидів від 2,4 до 4,8 тис. Т; V група - обсяг викидів понад 4,8 тис. Т.

По кожній групі обчислимо суму обсягів викидів та суму квадратів викидів.

Далі виконаємо процедуру розкладання обсягів викидів на складові частини за законом, розкладання варіацій, обчисливши всі види дисперсій - Do, D_m D_e за формулами:

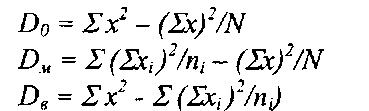
Для обчислення дисперсій необхідно знайти значення таких величин: ∑x, (∑x)², ∑x², (∑х_і)²,

∑(∑х_і)2 / n _i. Для їх розрахунку складається табл. 2.4.4. За даними цієї таблиці маємо:

Підставляємо ці дані в формули дисперсій:

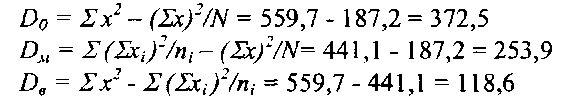
Розрахунок дисперсій дає такі результати :

Міжгрупова дисперсія набагато вища внутрішньогрупової дисперсії, яка обумовлена випадковістю варіації викидів. Тобто варіація викидів, обумовлена в основному дією систематичних факторів. Визначимо вплив на стан забруднення систематичних та випадкових факторів за ή і iή². Розрахунок кореляційного відношення і коефіцієнта детермінації дає змогу кількісно оцінити тісноту взаємодії і ступінь зв'язку між двома групами факторів :

тіснота взаємодії викидів із систематичними факторами складає:

Зробимо перевірку істотності зв'язку, яка ґрунтується на порівнянні фактичного значення ή²з його критичним значенням ή_ά² ,що знаходиться з математичних таблиць при заданому рівні істотності (ά=0,05) і ступенях вільності: V₁ = т-1 = 5-1=4, V₂ = N-m = 28-5=23

Критичне значення ή_ά² при 4 і 23 ступенях вільності для рівня істотності ά = 0,05 становить: ή²_0,05 (4;23) = 0,328.

Фактичне значення ή_в=0,318, що є < 0,328 і свідчить про те, що істотність між викидами і випадковістю не є доказаною. Тобто на варіацію викидів шкідливих речовин в атмосферне повітря впливають систематичні фактори. Порівнюючи фактичне значення ή_с = 0,682, що є набагато > 0,328, підтверджуємо факт наявності зв'язку викидів з систематичними факторами.

Перевірка істотності зв'язку здійснюється за допомогою F -критерію, який можна розрахувати за різними формулами:

Табличне (критичне) значення F-критерію знаходиться з математичних таблиць: F_0.05 (4;23) = 2,8. Фактичне значення F_c=12,3 > > F_0.05 ⁼ 2,8, що свідчить про істотність кореляційного зв'язку між викидами і систематичними факторами, яка є доказаною.

Висновки

Таким чином в Житомирській області 68,2 % варіації викидів шкідливих речовин в атмосферу пов'язані з різними систематичними факторами. Варіація за рахунок випадковості складає 31,8%.

Різниця групових середніх у цьому разі невипадкова і є свідченням про наявність зв'язку між викидами і систематичними факторами. Зроблені висновки надійні і достовірні, що можна гарантувати із ймовірністю помилкового висновку в 5-й випадках зі 100.

Але зауважимо, що кореляційне відношення має тенденцію дещо перебільшувати щільність зв'язку. Тому для більш точної оцінки щільності зв'язку слід використовувати коефіцієнт кореляції. Крім того конкретний вплив окремих систематичних факторів також розглядає кореляційний метод аналізу.

ПРАКТИЧНЕ ЗАВДАННЯ:

1. Для дисперсного аналізу використати показник обсягу викидів в атмосферу згідно з варіантом.

Динаміка викидів забруднюючих речовин в атмосферне повітря від стаціонарних джерел забруднення у регіоні по окремим населеним пунктам, тис.т

ВАРІАНТ	1	2	3	4	5
	2000	2005	2006	2007	2008
м.Черкаси	16,821	21,432	19,07	18,353	19,52
м.Ватутіне	0,817	1,267	1,054	1,065	0,857
м.Канів	0,115	0,09	0,096	0,079	0,097
м.Золотоноша	0,546	0,381	0,291	0,414	0,286
м.Сміла	1,31	1,75	1,541	0,708	0,533
м.Умань	0,79	1,031	0,871	1,315	1,315
Городищенський р-н	0,345	0,379	0,577	0,509	0,576
Драбівський р-н	0,112	0,039	0,187	0,249	0,467
Жашківський р-н	0,191	0,698	0,7	0,596	0,793
Звенигородський р-н	0,852	0,13	0,15	0,111	0,188
Золотоніський р-н	1,357	3,254	3,536	2,645	3,04
Кам'янський р-н	0,227	0,231	0,261	0,149	0,111
Канівський р-н	0,015	0,013	0,025	0,353	3,945
Катеринопільський р-н	0,264	0,086	0,059	0,047	0,065
К.Шевченківський р-н	0,402	0,478	0,399	0,553	0,47
Лисянський р-н	0,643	1,049	1,21	0,713	0,613
Маньківський р-н	0,26	0,121	0,207	0,177	0,379
Монастирищенський р-н	0,379	0,209	0,263	0,16	0,09
Смілянський р-н	0,201	0,276	0,37	0,564	0,496
Тальнівський р-н	0,816	2,151	2,086	1,846	1,573
Уманський р-н	0,476	0,373	0,312	0,502	0,502
Христинівський р-н	0,468	0,917	0,92	0,834	0,836
Черкаський р-н	0,411	1,709	2,146	2,407	2,278
Чорнобаївський р-н	0,4	0,815	2,855	3,553	3,305
Чигиринський р-н	0,228	0,039	0,073	0,073	0,058
Шполянський р-н	0,332	0,495	0,983	0,809	0,782

2. Заповнити таблицю «Допоміжні розрахунки для дисперсного аналізу»