МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика»

Т.С. Кули-Заде, Н.П. Наумов

ИЗУЧЕНИЕ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ

ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ

ПОЛУПРОВОДНИКОВ И МЕТАЛЛОВ

ФИЗИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНОЙ РАБОТЕ 408

Москва  2011

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика»

Т.С. Кули-Заде, Н.П. Наумов

ИЗУЧЕНИЕ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ

ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ

ПОЛУПРОВОДНИКОВ И МЕТАЛЛОВ

ФИЗИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНОЙ РАБОТЕ 408

Рекомендовано редакционно-издательским советом университета в качестве методических указаний для студентов ИУИТ, ИПСС и ИТТСУ

Москва  2011

УДК 621.382.2

Н-20

Кули-Заде Т.С., Наумов Н.П. Изучение температурной зависимости электрического сопротивления полупроводников и металлов. Физика. Методические указания к лабораторной работе 408. – М.: МИИТ, 2011. – 12 с.

Методические указания к выполнению лабораторной работы 408 «Изучение температурной зависимости электрического сопротивления полупроводников и металлов» соответствует программе и учебным планам по физике (раздел «Физика твердого тела») и предназначены для студентов 2, 3 курсов технических специальностей.

© Московский государственный

университет путей сообщения

(МИИТ), 2011

Учебно-методическое издание

Кули-Заде Тофик Салман-оглы

Наумов Николай Павлович

Изучение температурной зависимости электрического

сопротивления полупроводников и металлов.

Физика. Методические указания к лабораторной работе 408

Подписано в печать Усл.-печ. л. – 6,0

Формат 60х84/16. З аказ –

Изд. № 247-об Тираж 200 экз.

Работа 408

ИЗУЧЕНИЕ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ

ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ

ПОЛУПРОВОДНИКОВ И МЕТАЛЛОВ

Цель работы. Изучение зависимости электрического сопротивления полупроводников и металлов от температуры.

Приборы и принадлежности. Лабораторная установка ФПК-07. Блок-схема установки приведена на рис. 1.

1 – блок с образцами, 2 – измерительный блок.

Рис. 1.

Введение

Плотность тока в проводнике равна произведению удельной электрической проводимости металла  на напряженность электрического поля :

  . (1)

Выражение (1) – закон Ома в дифференциальной форме, связывающей плотность тока в любой точки внутри проводника с напряженностью электрического поля в этой точке. В выражении (1) величина

  ,

обратная удельному сопротивлению , для электронных проводников и, в частности, для металлов равна

  , (2)

где – заряд электрона, – концентрация электронов, – масса электрона,  – время релаксации электронного газа к равновесному состоянию.

Из выражения (2) следует, что проводимость материала тем выше, чем больше концентрация свободных электронов. В металлах концентрация свободных электронов остается постоянной с изменением температуры и других видов воздействия. Зависимость проводимости от температуры определяется уменьшением  с увеличением температуры. Действительно,

  , (3)

где – средняя длинна свободного пробега электрона (для металлов  10^8 м), а – средняя скорость теплового движения электронов.

Там как согласно экспериментальным данным

 ,

а для классического электронного газа

 ,

получаем:

  T^3/2, или   T^3/2. (4)

Следовательно, в случае классической физики сопротивление металла должно изменяться не линейно, как показывают эксперименты, а по закону T^3/2.

Типичная экспериментальная зависимость сопротивления металлов от температуры представлена на рис. 2.

Из рис. 2 следует, что в широком диапазоне температур сопротивление металлов линейно растет с ростом температуры. Увеличение величины сопротивления R объясняется тем, что с ростом температуры Т амплитуда тепловых колебаний кристаллической решетки увеличивается, и столкновение электронов с решеткой происходят чаще. Наличие остаточного нулевого сопротивления R_ОСТ в области низких температур связано с наличием дефектов и примесей, искажающих кристаллическую структуру материала.

Таким образом, классическая физика дает для металлов неправильную температурную зависимость R(T). Линейная зависимость может быть объяснена только с использованием модели вырожденного или квантового электронного газа в рамках квантовой физики.

Величина температурного коэффициента сопротивления

_R 

для большинства металлов составляет от 110^3 К^1 до 510^3 К^1. Для чистых (беспримесных) металлов величина температурного коэффициента близка к значению К^1.

Линейная зависимость сопротивления металлов от температуры позволяет реализовывать на их основе проволочные измерители температур в широком температурном диапазоне.

Наибольшие значения _R достигаются в полупроводниковых материалах, что связано с резкой температурной зависимостью концентрации свободных носителей:

n  exp ,

однако сама температурная зависимость R(T) имеет нелинейный характер. Кроме того, диапазон изменяемых температур в случае полупроводниковых терморезисторов весьма ограничен.

Полупроводники – это большой класс веществ, сопротивление которых изменяется в широких пределах и в очень сильной степени зависит от температуры (по экспоненциальному закону). Электропроводимость нелегированного (собственного) проводника называется собственной проводимостью. Она обусловлена тепловым переводом электронов из валентной зоны в свободную зону полупроводника, которая становится при этом зоной проводимости. Электронная проводимость (проводимость п-типа) возникает при тепловом переходе электронов с донорных уровней в зону проводимости. При температуре абсолютного нуля все энергетические уровни в зоне проводимости (в свободной зоне) были бы свободны (вакантны), зона проводимости отделена от полностью заполненной валентной зоны запрещенной энергетической зоной с шириной Е_g. По мере возрастания температуры электроны валентной зоны из-за термического возбуждения переходят в зону проводимости, при этом в валентной зоне возникает вакантное энергетическое состояние или «дырка».

Электроны в зоне проводимости и дырки в валентной зоне определяют электропроводность собственных полупроводников.

Температурная зависимость концентрации электронов в зоне проводимости, а, следовательно, и концентрации образовавшихся при этом дырок в собственном полупроводнике определяется соотношением

n  n₀ . (5)

Тогда удельная электропроводность собственных полупроводников изменяется по закону :

  ₀ . (6)

У величение проводимости полупроводников с ростом температуры – главное отличие полупроводников от металлов. С точки зрения зонной теории это обстоятельство объясняется довольно просто: с повышением температуры растет число электронов, которые из-за теплового возбуждения переходят в зону проводимости. Поэтому удельная электропроводность собственных и примесных полупроводников резко возрастает с ростом температуры, а электрическое сопротивление – резко уменьшается.

Если представить зависимость ln как функцию 1/T, то для собственных полупроводников она представляет прямую (рис. 4), по наклону которой можно определить ширину запрещенной зоны Е_g, экстраполируя данную зависимость в область малых значений 1/T. Зависимость сопротивления полупроводников от температуры описывается следующим выражением (при условии, что геометрические размеры образца с температурой не изменяются):

R  R₀ , (7)

где R₀ – некоторая константа.

Прологарифмировав выражение (7), получим:

lnR  lnR₀  . (8)

Формула (8) представляет уравнение прямой в координатах lnR и 1/T. Построив в этих координатах график зависимости сопротивления полупроводника от температуры, получим прямую линию, как показано на рис. 4.

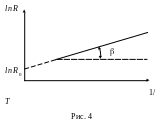
Продолжение прямой до пересечения с осью ординат lnR определяет значение lnR₀. Тангенс угла наклона прямой к оси абсцисс определяет величину постоянной B  tg:

B  . (9)

Данное выражение позволяет определить значение ширины запрещенной зоны:

Е_g  2kB. (10)

Порядок выполнения работы

I. Температурная зависимость электрического сопротивления полупроводников

1. Включите установку 1 нажатием тумблера «Сеть» на передней панели и установку 2 нажатием тумблера «Сеть» на задней панели.

2. Поставьте переключатель «Образец» на установке 1 в положение 3, что соответствует полупроводниковому термистору.

3. Занесите в таблицу 1 значения температуры (правая шкала на установке 2) и сопротивления термистора (левая шкала на установке 2).

4. Включите термостат нажатием кнопки «Нагрев», при этом должен загореться светодиод.

5. Отметьте по прибору температуру внутри нагревателя (по достижении t  30 C) и одновременно снимите показания сопротивления термистора. Измерения повторите 10 раз через каждые 5 ºС, результаты измерений R и t занесите в таблицу 1.

6. Отключите термостат (светодиод погаснет) и включите вентилятор, нажав кнопку «Вентилятор» (загорится светодиод).

7. Проведите те же измерения при охлаждении термистора для тех же значений температуры.

8. Для каждой величины вычислите среднее(при нагреве и остывании) значение электрического сопротивления.

9. Постройте график зависимости сопротивления от температуры , нанося по оси абсцисс температуру t, C, а по оси ординат сопротивления R, кОм (откладывая по оси ординат средние значения сопротивлений, полученных при нагревании и при охлаждении термистора).

10. Если измерения делались для двух термисторов, то постройте графики для каждого из них.

11. Переведите температуру из градусов Цельсия в кельвины и вычислите величину , причем расчет величины сделайте до пятого знака после запятой (например,  0,00335). Занесите полученные значения натуральных логарифмов lnR в таблицу 1.

12. Постройте зависимость сопротивления термисторов от температуры в координатах lnR и 10⁴ или 10⁵.

13. Из полученных зависимостей определите наклон прямой, то есть постоянную В из формулы (10), выразив её в кельвинах, и рассчитайте значение ширины запрещенной зоны Е_g в электрон-вольтах по формуле (10). В связи с тем, что k  1,3810^23 ДжК^1, здесь k  0,8610^4 эВК^1, поскольку 1эВ  1,610^19 Дж.

Таблица 1

ТЕРМИСТОР
№ п.п.	t, С	T, К	R, кОм		RСР, кОм	 104, К1	lnRСР
			НАГРЕВ	ОХЛАЖДЕНИЕ
1
2
10
Ширина запрещённой зоны Еg  эВ