Задание 3. Определение показателя преломления призмы

При прохождении светового пучка через призму (рис. 1.7) существует угол падения, при котором отклонение пучка от начального направления минимально. При этом лучи падающего и прошедшего пучков симметричны относительно преломляющих граней призмы. Угол минимального отклонения - наименьший угол между оптической осью и преломленным лучом – связан с преломляющим углом призмы соотношением:

. (1.20)

При этом угол падения определяется законом преломления:

, (1.21)

тогда показатель преломления находится по формуле:

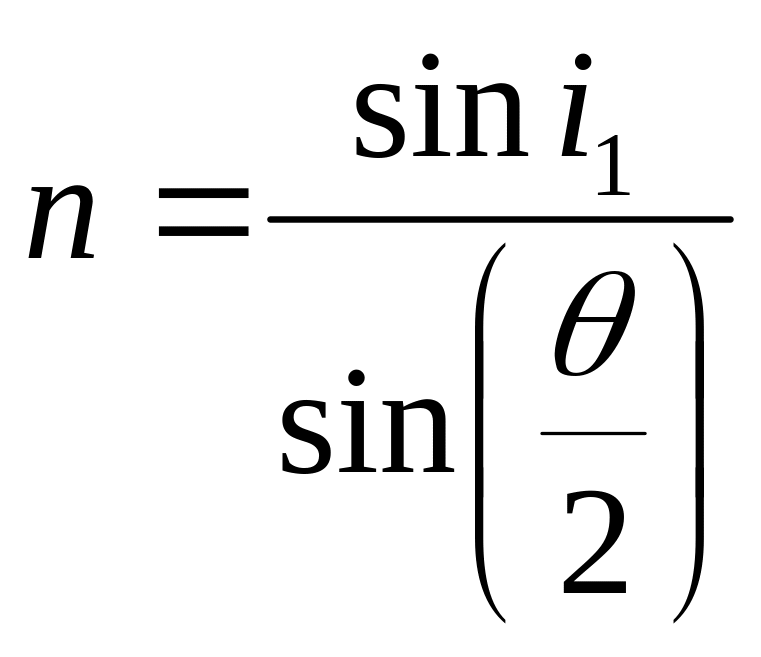. (1.22)

Эксперимент

1. Освободите оптическую скамью, установите на нее поворотный стол (модуль 13), так, чтобы его риска была вблизи отметки 20 см, и поместите призму (объект 9) в объектную плоскость стола. Поворачивая стол, наблюдайте на экране установки движение пучков, отраженных от граней призмы, и преломленных в ней (рис. 1.8).

Рис. 1.8

2. Поворачивая стол, направьте отраженный от грани луч навстречу падающему, совместив следы соответствующих пучков в точке выхода луча из лазера. При этом фиксируется положение нормали к грани призмы. Зафиксируйте угловую координату стола.

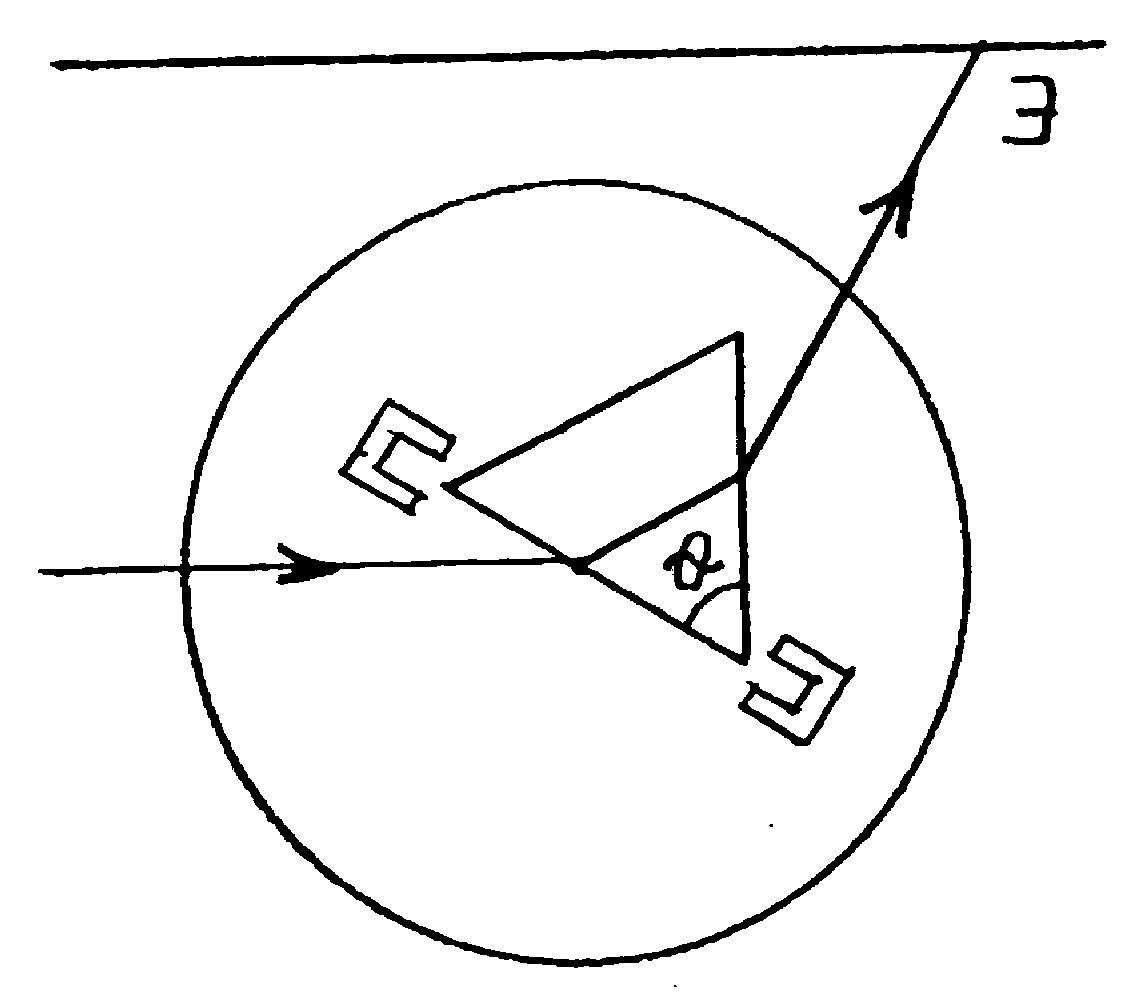
3. Поверните стол против часовой стрелки до фиксации положения нормали к следующей грани призмы. Смещение стола представляет собой угол, смежный с ближайшим к вам преломляющим углом призмы . Тогда данный преломляющий угол призмы .

4. Пользуясь тем же методом, найдите остальные преломляющие углы призмы..

5. Определив положение нормали к основанию призмы – зафиксировав угловую координату стола , поворачивайте стол таким образом, чтобы световое пятно на экране перемещалось вправо, до тех пор, пока не получите минимальное отклонение преломленного луча – самое удаленное (крайнее правое) положение светового пятна на шкале экрана.

6. Снимите координату стола и определите угол падения .

7. По формуле (1.22) найдите показатель преломления.

8. Выполните пункты 5-7 для боковой грани призмы.

9. Вычислить , , , и занести результаты в таблицу:

грань	º	º	º	º	º					, %
основание
боковая

10. Представить окончательный результат в виде:

, …%

Сделайте вывод о проделанной работе.

Контрольные вопросы

1. Сформулируйте законы геометрической оптики.

2. Каков физический смысл абсолютного и относительного показателей преломления?

3. Показать эквивалентность двух формулировок принципа Ферма.

4. Вывести законы отражения и преломления света на основе принципа Ферма.

5. Выведите формулы 1.7 и 1.19.

6. Объясните, почему в задании 3 смещение стола представляет собой угол, смежный с преломляющим углом призмы?

7. Выведите соотношение (1.20).

8. Какова скорость света в использованных в работе веществах?

9. Рассчитайте угол полного внутреннего отражения от граней призмы.

Литература

Лабораторная работа № 2

Определение фокусного расстояния и увеличения линз

Цель работы: ознакомление с методами определения фокусного расстояния и увеличения линз.

Оборудование: модули: конденсор с экраном 5, объектив 6, микропроектор 2, кассета в двухкоординатном держателе 8; объекты: калибровочная сетка 2.

Краткая теория

Тонкие линзы. Построение изображений.

Линзой называется шлифованное стекло или любое другое прозрачное вещество, ограниченное с двух сторон сферическими поверхностями; в частном случае одна из поверхностей линзы может быть плоской. Линзы разделяются на два класса: собирающие, или выпуклые, когда сферическая поверхность выпуклая, и рассеивающие, или вогнутые, когда сферическая поверхность вогнутая. Эти определения применимы для линз, имеющих больший коэффициент преломления, чем среда, из которой падают лучи.

Сферические линзы применяются для получения изображений и собирания световых пучков.

Линзы бывают толстые и тонкие. Тонкой называется линза, толщина которой мала по сравнению с радиусами кривизны ограничивающих ее поверхностей.

Рассмотрим тонкую собирающую линзу (рис. 2.1а).

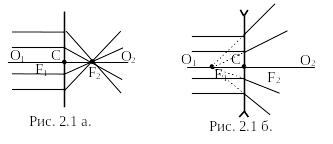
На рисунке С – оптический центр – точка, проходя через которую лучи не изменяют направления.

Всякая прямая, проходящая через оптический центр, называется оптической осью, и если она, кроме того, проходит через центры кривизны (О₁ и О₂) – главной оптической осью. Плоскость, перпендикулярная главной оптической оси и проходящая через оптический центр, называется главной плоскостью линзы.

Главным фокусом линзы называется точка, в которой пересекаются после преломления в линзе лучи, падающие на нее пучком, параллельным главной оптической оси (на рис. 2.1 точки F₁ и F₂). Расстояние f от главного фокуса до оптического центра линзы (расстояние СF₂ и СF_1`) называется главным фокусным расстоянием и является основной характеристикой линзы. Для собирающих линз главное фокусное расстояние – величина положительная, для рассеивающих - отрицательная. Часто линзу характеризуют оптической силой D = 1/f в диоптриях – величиной, обратной главному фокусному расстоянию, выраженному в метрах. Для рассеивающих линз главный фокус является мнимым, и для его отыскания берут не сами лучи, а их продолжения (рис. 2.1 б).

Для построения изображения предмета с помощью линзы пользуются лучами, ход которых через линзу известен. Обычно берут два луча из следующих трех (рис. 2.2): луч 1, проходящий через оптический центр (он пройдет через линзу, не преломляясь); луч 2, падающий на линзу параллельно ее главной оптической оси (этот луч при выходе из собирающей линзы пройдет через ее главный фокус, см. рис. 2.2 а, а при выходе из рассеивающей линзы пойдет так, что его продолжение пройдет через главный фокус, см. рис. 2.2 б); луч 3, проходящий через главный фокус собирающей линзы (рис. 2.2 а) или луч, продолжение которого проходит через главный фокус рассеивающей линзы (рис. 2.2 б) (этот луч выходит из линзы параллельно главной оптической оси).

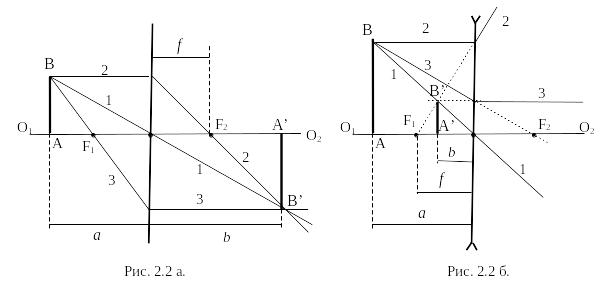
Изображение предмета в зависимости от класса линзы и от расстояния от предмета до линзы может получиться увеличенным (рис. 2.2 а) или уменьшенным (рис. 2.2 б), действительным (рис. 2.2 а) или мнимым (рис. 2.2 б). Мнимым изображением предмета называется такое его изображение, которое формируется продолжениями лучей, преломленных линзой, и находится перед линзой по одну сторону с предметом. Рассеивающая линза всегда дает мнимое уменьшенное изображение предмета. Вид изображения, созданного собирающей линзой, зависит от соотношения между расстоянием от предмета до линзы а и фокусным расстоянием линзы f:

a < f	Изображение мнимое увеличенное.
a = f	Изображения нет (изображение локализовано на бесконечности).
f < a < 2f	Изображение действительное, увеличенное.
а = 2f	Изображение действительное в масштабе 1:1.
a > 2f	Изображение действительное, уменьшенное.

Обозначим через b (рис. 2.2) расстояние от линзы до изображения. Зависимость между a, b и f дается формулой тонкой линзы:

. (2.1)

Линейное увеличение, даваемое тонкой линзой,

, (2.2)

т.е. линейным увеличением называется отношение размера изображения предмета к соответствующему размеру предмета.