1. Вектор лежит в плоскости падения электромагнитной волны.

Направления векторов , и для какого-то момента времени показаны на рис. 9.1 ( - вектор Умова-Пойтинга).

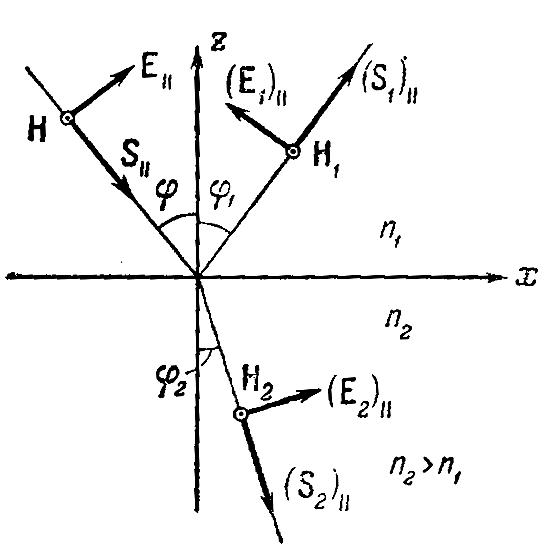
Рис. 9.1. Направления векторов и на границе раздела.

Вектор лежит в плоскости падения.

Направление векторов , и определяется выбором направления для , и . В данном случае векторы , и направлены одинаково — перпендикулярно к плоскости чертежа по направлению к читателю. Для проекций амплитуд векторов и имеем:

.

Учитывая, что , , , а также , находим:

(9.1)

Тогда

(9.2)

Складывая уравнения (2.1), получаем:

,

откуда

. (9.3)

2. Вектор перпендикулярен к плоскости падения волны.

В этом случае выберем направление векторов , и согласно рис. 9.2. На нем векторы , и направлены от читателя перпендикулярно к плоскости чертежа.

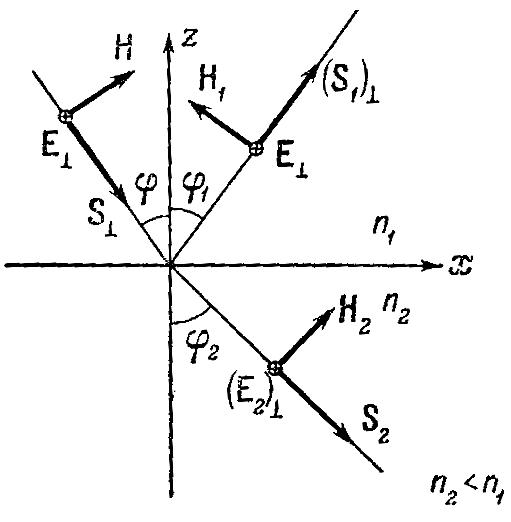
Рис. 9.2. Направления векторов и на границе раздела.

Вектор перпендикулярен плоскости падения луча.

Для проекций амплитуд исследуемых векторов на оси получим соотношения

Последнее условие можно переписать в виде

.

Отсюда легко получаются искомые зависимости

, . (9.4)

Займемся анализом найденных соотношений. Прежде всего рассмотрим относительные интенсивности отраженной и преломленной волн. Проанализируем зависимость коэффициента отражения от угла падения (рис 9.3).

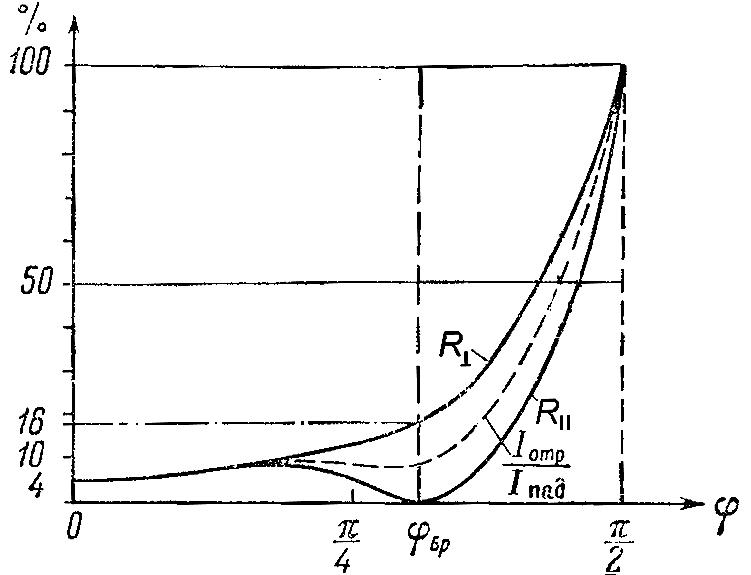
Рис.9.3. Зависимость коэффициента отражения R от угла падения

При переходе света из воздуха (n₁1) в стекло (n₂1,5).

Рассмотрение формул Френеля показывает, что компоненты , и , по-разному изменяются с увеличением угла . Во-первых, сразу видно, что если , то и, следовательно, . Вместе с тем коэффициент отражения не обращается в нуль при , так как знаменатель выражения (2.4) . Таким образом, получается, что при некотором значении угла падения от гра­ницы раздела отразится только электромагнитная волна с вполне определенной поляризацией. Волна, в которой колебания вектора параллельны плоскости падения, вообще не отразится при . Вектор в отраженной волне (при выполнении условия ) будет колебаться перпендикулярно к плоскости падения. В учебниках по оптике часто употребляют несколько иную терминологию. Так, например, в рассматриваемом случае говорят, что отраженный свет поляризован в плоскости падения. Отсюда видно, что плоскость по­ляризации света соответствует плоскости, перпендикулярной к направлению колебаний вектора .

Для данного случая, впервые экспериментально обнаруженного Малю, очевидны следующие соотношения: если , то и, значит,

.

Эта зависимость угла, при котором наблюдается плоская поляризация отраженной волны, от отношения показателей преломления двух исследуемых диэлектриков носит название закона Брюстера, а соответствующий угол часто называют углом Брюстера . В этих обозначениях

. (9.5)

Для перехода световой волны (видимая область спектра) из воздуха в стекло , что соответствует углу .

Заметим, что отражение полностью поляризованной волны наблюдается тогда, когда нормали к преломленной и отраженной волнам взаимно перпендикулярны (рис. 9.4).

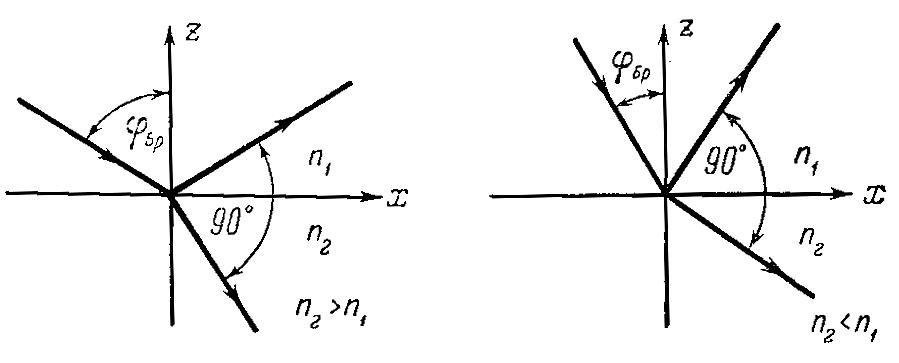
Рис. 9.4. Нормали к преломленной и ораженным волнам при падении света

на границу раздела двух сред под углом Брюстера перпендикулярны.

Если связывать наличие отраженной волны с вынужденными колебаниями электронов во второй среде, то в направлении, перпендикулярном к нормали к преломленной волне, не должна распространяться энергия, так как электрон не излучает в направлении, вдоль которого происходят его колебания (рис. 9.5).

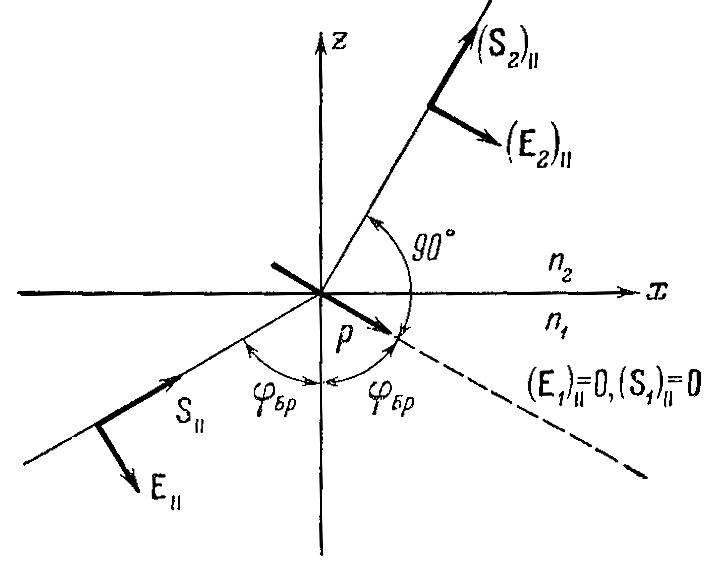
Рис. 9.5. К трактовке закона Брюстера с позиций электронной теории.

Вектор в падающей волне лежит в плоскости падения. Отраженная волна этой gоляризации отсутствует, т.к. электроны не излучают в направлении своих колебаний.

Легко заметить, что последнее ограничение относится лишь к колебаниям электронов в плоскости падения волны, происходящим в результате действия на них . Вместе с тем будет раскачивать электроны в направлении, перпендикулярном к плоскости падения, и такое излучение будет распространяться без всяких ограничений в направлении, удовлетворяющей условию (9.5), целиком определяя поляризацию отраженной волны.