
- •Физический практикум оптика
- •Введение
- •Лабораторный оптический комплекс лко-3п
- •Функциональные модули
- •Набор объектов
- •Настройка установки
- •1.2. Прохождение света через плоскопараллельную пластинку.
- •1.3. Преломление света в призме.
- •1.4. Принцип Ферма.
- •Порядок выполнения работы Задание 1. Преобразование пучка света линзами
- •Эксперимент
- •Задание 2. Определение показателя преломления пластины
- •Эксперимент
- •Задание 3. Определение показателя преломления призмы
- •Эксперимент
- •Контрольные вопросы
- •Порядок выполнения работы Задание 1. Калибровка микропроектора
- •Задание 2. Определение фокусного расстояния объектива
- •Задание 3. Определение фокусного расстояния и увеличения объектива с помощью калибровочной сетки.
- •Контрольные вопросы
- •Порядок выполнения работы
- •Эксперимент
- •Задание 2. Интенсивность в сферической волне
- •Эксперимент
- •Контрольные вопросы
- •Изучение интерференции световых волн с помощью щелей Юнга
- •Краткая теория
- •4.1. Интерференция света: общие сведения.
- •4.2. Опыт Юнга.
- •Задание 1. Изучение интерференции. Эксперимент
- •Задание 2. Измерение длины волны лазерного излучения. Эксперимент
- •Контрольные вопросы
- •Контрольные вопросы
- •Дифракция Френеля
- •Краткая теория
- •6.1. Геометрическая оптика и дифракция.
- •Угол дифракции
- •Длина дифракции
- •Дифракция Френеля и дифракция Фраунгофера
- •6.2. Дифракция Френеля.
- •6.3. Дифракция Френеля на круглом отверстии и диске.
- •Порядок выполнения работы Задание 1. Наблюдение дифракции Френеля на диске.
- •Эксперимент
- •Задание 2. Дифракция Френеля на круглом отверстии. Зоны Френеля.
- •Эксперимент
- •Контрольные вопросы
- •Дифракция Фраунгофера
- •Краткая теория
- •7.1. Дифракция Фраунгофера на одной щели.
- •7.2. Дифракция Фраунгофера на дифракционной решетке.
- •Порядок выполнения работы Задание 1. Дифракция Фраунгофера на щели Эксперимент
- •Задание 2. Дифракция Фраунгофера на одномерной дифракционной решетке
- •Контрольные вопросы
- •Изучение поляризации света. Экспериментальная проверка закона Малюса.
- •Краткая теория
- •1. Плоская или линейная поляризация.
- •Порядок выполнения работы
- •Задание 1. Определение степени поляризации излучения лазера.
- •Задание 2 Экспериментальная проверка закона Малюса
- •Задание 3. Определение коэффициентов пропускания неидеального поляризатора.
- •Контрольные вопросы
- •Литература
- •Лабораторная работа №9 Экспериментальная проверка закона Брюстера
- •Краткая теория
- •1. Вектор лежит в плоскости падения электромагнитной волны.
- •2. Вектор перпендикулярен к плоскости падения волны.
- •Порядок выполнения работы
- •Эксперимент
- •1. Установка оборудования.
- •2. Калибровка установки.
- •3. Измерения.
- •Контрольные вопросы
- •Литература
- •Лабораторная работа №10 Изучение явления вращения плоскости поляризации света
- •Краткая теория
- •Порядок выполнения работы
- •Эксперимент Задание 1. Определение степени поляризации излучения лазера.
- •Задание 2. Измерение концентрации сахара в растворе.
- •Контрольные вопросы
- •Литература
- •Содержание
Контрольные вопросы
Дать определения угла дифракции и длины дифракции.
При каком условии перестают выполняться законы геометрической оптики?
Чем отличается дифракция Френеля от дифракции Фраунгофера? Что является критерием наблюдения того или иного типа дифракции?
Дать определение зон Френеля? Вывести формулу для радиусов зон Френеля (6.17).
Как связаны между собой амплитуда и интенсивность света, пришедшего в точку наблюдения от одной только центральной зоны Френеля и от всей волновой поверхности?
Объяснить механизм возникновения дифракционной картины при дифракции Френеля на диске. В каком случае в центре тени, отбрасываемом диском, будет наблюдаться светлое пятно? Почему?
Объяснить механизм возникновения дифракционной картины при дифракции Френеля на круглом отверстии. В каких случаях в центре дифракционной картины будет наблюдаться светлое пятно, и в каких случаях будет наблюдаться темное пятно? Почему?
Почему для получения плоской волны при выполнении упражнения 2 объектив устанавливают за линзой-конденсором на расстоянии, равном фокусному расстоянию объектива?
Лабораторная работа №7
Дифракция Фраунгофера
Цель работы: изучить экспериментально закономерности дифракции Фраунгофера на одной щели и на одномерной дифракционной решетке.
Оборудование: модули: микропроектор 2, линза-конденсор 5, объектив 6, двухкоординатный держатель 8; объекты: экраны с щелями 23, 27, 29, 30, одномерная дифракционная решетка 32.
Краткая теория
7.1. Дифракция Фраунгофера на одной щели.
Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики.
Условия наблюдения дифракционных явлений, объяснение явления дифракции на основе принципа Гюйгенса-Френеля, а также особенности дифракции сферической световой волны на отверстии и на диске разобраны в краткой теории к предыдущей лабораторной работе (разделы 6.1 – 6.3). В настоящей работе будет рассмотрена дифракция плоских световых волн, или дифракция в параллельных лучах, так же называемая дифракцией Фраунгофера, которая наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызывающего дифракцию. Чтобы этот тип дифракции осуществить на практике, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.
Рассмотрим дифракцию Фраунгофера от бесконечно длинной щели (для этого практически достаточно, чтобы длина щели b была значительно больше ее ширины а). Пусть плоская монохроматическая волна падает нормально к плоскости узкой щели (рис. 7.1). Оптическая разность хода между крайними лучами MC и ND, идущими от щели в произвольном направлении θ,
![]() , (7.1)
, (7.1)
где F – основание перпендикуляра, опущенного из точки М на луч ND.
Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля (см. раздел 6.2), имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна λ/2, т.е. всего на ширине щели уместится 2Δ/λ зон. Так как свет падает на щель нормально, то плоскость щели совпадает с фолновым фронтом; следовательно, все точки волнового фронт в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.
Из выражения (7.1) вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла θ. От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. При интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга. Следовательно, если число зон Френеля четное, то
![]() (m
= 1, 2, 3, …), (7.2)
(m
= 1, 2, 3, …), (7.2)
и в точке Р наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное, то
![]() (m
= 1, 2, 3, …), (7.3)
(m
= 1, 2, 3, …), (7.3)
и
наблюдается дифракционный
максимум,
соответствующий действию одной
нескомпенсированной зоны Френеля.
Отметим, что в направлении
![]() щель действует как одна зона Френеля,
и в этом направлении свет распространяется
с наибольшей интенсивностью, т.е. в точке
Р0
наблюдается центральный
дифракционный максимум.
щель действует как одна зона Френеля,
и в этом направлении свет распространяется
с наибольшей интенсивностью, т.е. в точке
Р0
наблюдается центральный
дифракционный максимум.
Из
условий (7.2) и (7.3) можно найти направления
на точки экрана, в которых амплитуда (а
следовательно и интенсивность) света
равна нулю (![]() )
или максимальна (
)
или максимальна (![]() ).
Распределение интенсивности на экране,
получаемое вследствие дифракции
(дифракционный спектр) показано на рис.
7.2. Интенсивность света Iθ
в точке, расположение которой
характеризуется углом θ и интенсивность
I0
в точке Р0,
расположенной в центре дифракционной
картины (против центра линзы) связаны
между собой соотношением
).
Распределение интенсивности на экране,
получаемое вследствие дифракции
(дифракционный спектр) показано на рис.
7.2. Интенсивность света Iθ
в точке, расположение которой
характеризуется углом θ и интенсивность
I0
в точке Р0,
расположенной в центре дифракционной
картины (против центра линзы) связаны
между собой соотношением
![]() . (7.4)
. (7.4)
График
функции (7.4) показан на рис. 7.2. Расчеты
по данной формуле показывают, что
интенсивности в центральном и последующих
максимумах относятся как
1:0,047:0,017:0,0083:…, т.е. основная часть световой
энергии сосредоточена в центральном
максимуме. Из опыта и соответствующих
расчетов следует, что сужение щели
приводит к тому, что центральный максимум
расплывается, а интенсивность уменьшается
(это относится и к другим максимумам).
Наоборот, чем щель шире (а
> λ),
тем картина ярче, но дифракционные
полосы уже, а число самих полос больше.
При
![]() в центре получается резкое изображение
источника света, т.е. имеет место
прямолинейное распространение света.
в центре получается резкое изображение
источника света, т.е. имеет место
прямолинейное распространение света.
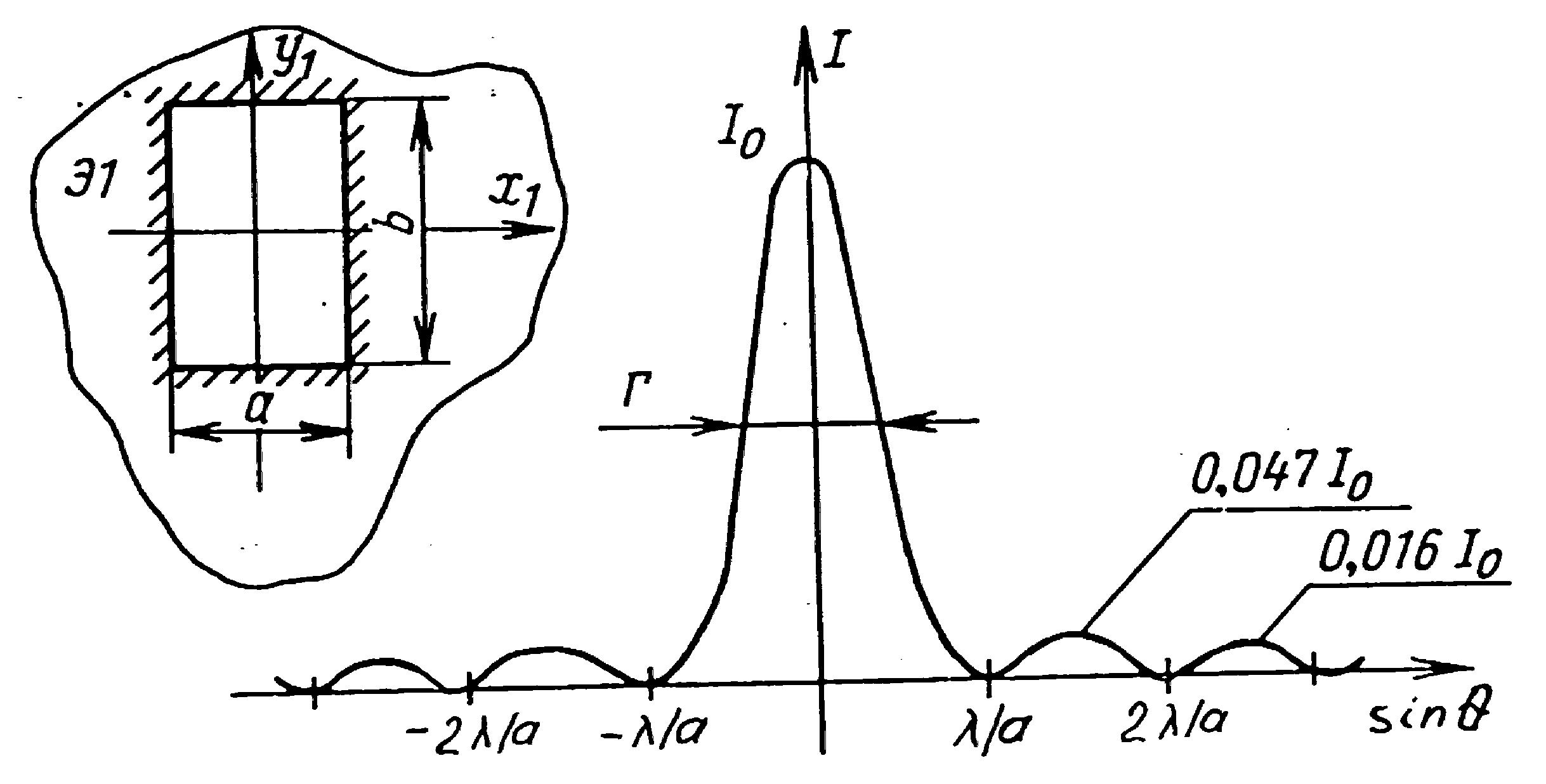
Рис. 7.2.
