6. Сжатие данных при помощи сетей встречного распространения.
В сети Кохонена происходит решение задачи нахождения кластеров в пространстве входных образов. Сеть Кохонена обучается без учителя на основе самоорганизации. В течении обучения вектора весов нейронов стремятся к центрам кластеров – групп векторов обучающей выборки. После обучения сеть сопоставляет предъявляемый образ к одному из кластеров, то есть к одному из выходов. В общем случае задача кластеризации представляется следующим образом:
-
есть объекты, характеризуемые
вектором параметров
,
имеющих
компонент 
;
-
есть введенное множество классов 
в
пространстве классов 
(обычно 
,
в случае 
,
задача сводится к тривиальной);
Необходимо
определить ядра классов 
в
пространстве классов
,
так что бы меры близости 
были
минимальны, то есть:
Обычно 
есть
евклидова мера 
.
Функция 
,
определяющая номер класса по
индексу 
множества
объектов {
}
, задает разбиение на классы и является
решением задачи классификации.
Например,
для задачи разбиения учеников на группы
{отличник, хорошист, троечник, двоечник}
по 
предметам,
центрами групп будут 
, 
и
так далее.
Сеть Кохонена выглядит, как показано на рисунке:
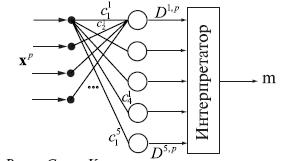
Ядра 
являются
весовыми коэффициентами нейронов.
Каждый нейрон сети Кохонена запоминает
один класс, то есть величина выхода тем
выше, чем ближе предъявляемый образец
к данному классу. Суть интерпретатора
– выбрать номер нейрона с максимальным
выходом (может не показываться). Если
использовать функцию SOFTMAX,
то выход можно трактовать как вероятность.
Меняя количество нейронов, мы можем
динамично менять количество классов.
Присвоение начальных значений происходит с помощью генератора случайных чисел – каждому весу присваивается небольшое значение. Однако для сети Кохонена желательно, чтобы значения весов изначально были равномерно распределены, для этого используется метод выпуклой комбинации.
Обучение сети Кохонена происходит следующим образом:
подаем на вход один из векторов ;
рассчитываем выход слоя Кохонена и определяем номер выигравшего нейрона
,
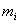выход которого максимален;корректируем веса только выигравшего нейрона
:
-
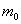скорость обучения, обычно используется
монотонно убывающая функция 
.
Обучение происходит пока не застабилизируются веса.
Звезды Гроссберга
Нейрон
в виде входной звезды имеет 
входов 
,
которым соответствуют веса 
и
один выход 
,
являющийся взвешенной суммой входов.
Входная звезда обучается выдавать на
выход сигнал, когда на входы поступает
определенная комбинация входов, по сути
входная звезда является детекторов
совокупного состояния входов. Процесс
обучения представляется в следующей
итерационной форме:
обычно 
и
монотонно убывает в течении обучения.
В процессе обучения (или лучше, в данном
случае, сказать - настройки) нейрон
учится усредненным обучающим векторам.
Выходная
звезда Гроссберга выполняет противоположную
функцию – командного нейрона, выдавая
на выходе определенную комбинацию при
поступлении сигнала на вход. Нейрон
этого типа имеет один вход 
и 
выходов 
,
которые обучаются по формуле:
Рекомендуется
брать 
равным
единице и постепенно уменьшать в ходе
обучения.
Особенность нейронов в виде звезд Гроссбега – локальная память: каждый нейрон в виде входной звезды помнит свой образ и игнорирует остальные. Если выходная звезда также присуща определенная команда.
Существует также интересный симбиоз сети Кохонена и звезды Гроссберга, получившая название «сеть встречного распространения». Слой Кохонена в данном случае работает в режиме интерполяции или аккредитации. Все слои полносвязны. Сеть представлена на рис.
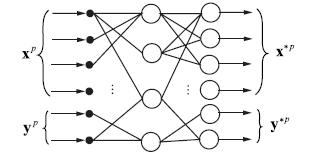
Рис. Сеть встречного распространения
Слой Гроссберга предназначен для совместной работы со слоем, дающим единственную единицу на выходе (как у слоя Кохонена в режиме аккредитации) или же такой набор выходов, что их сумма равна единице (функция SOFTMAX). Нейроны слоя Гроссберга вычисляют взвешенную сумму своих входов. Функция активации – линейная. Слой Гроссберга дает на выходе линейную комбинацию своих векторов весов, коэффициенты комбинации задаются входами слоя Гроссберга. Обычно данную сеть используют для сжатия данных. Более подробно о данной сети можно прочитать в специальной литературе.