2). Далее решаем уравнение, применяя общий алгоритм:

a⁰. Находим первообразную функции М = :

u(x,y)= +φ(y)= – + +φ(y)=

=xsiny+ycosx+ln|x|+φ(y). (1)

a¹. Подберем φ(y) так, чтобы выполнялось условие: = N(x,y); это значит, что выполняется: (xsiny+ycosx+ln|x|)+φ′(y)=xcosy+cosx+φ′(y)=N(x,y). (2)

a². Используя (2), запишем равенство для вычисления функции φ′(y):

φ′(y)=N(x,y)–(xcosy+cosx)= – . (3)

a³. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):

φ(y)=–ln|y|. (4)

a⁴. Запишем общее решение заданного уравнения:

u(x,y)= + = xsiny+ycosx+ln|x|–ln|y|= С. (5)

Ответ: u(x,y)= xsiny+ycosx+ln| |= С – общее решение.

Пример 6–143: Решить ДУ: (xcos2y+1)dx–x²∙sin2y∙dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.

Решение:

1). В нашем случае: =–2x∙sin2y и =–2x∙sin2y → условие = выполняется → задано уравнение в полных дифференциалах.

2). Далее решаем уравнение, применяя общий алгоритм:

a⁰. Находим первообразную функции М = :

u(x,y)= +φ(y)= +φ(y)= x²cos2y+x+φ(y). (1)

a¹. Подберем φ(y) так, чтобы выполнялось условие: = N(x,y); это значит, что выполняется: ( x²cos2y+x)+φ′(y)= –x²∙sin2y+φ′(y)=N(x,y). (2)

a². Используя (2), запишем равенство для вычисления функции φ′(y):

φ′(y)=N(x,y)+ x²∙sin2y=0. (3)

a³. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):

φ(y)=C. (4)

a⁴. Запишем общее решение заданного уравнения:

u(x,y)= + = x²cos2y+x= С. (5)

Ответ: u(x,y)= x²cos2y+x= С – общее решение.

Пример 7–181: Найти уравнение кривой, проходящей через точку (1,2), если произведение абсциссы точки касания на абсциссу точки пересечения нормали с осью ОХ равно удвоенному квадрату расстояния от начала координат до точки касания.

Р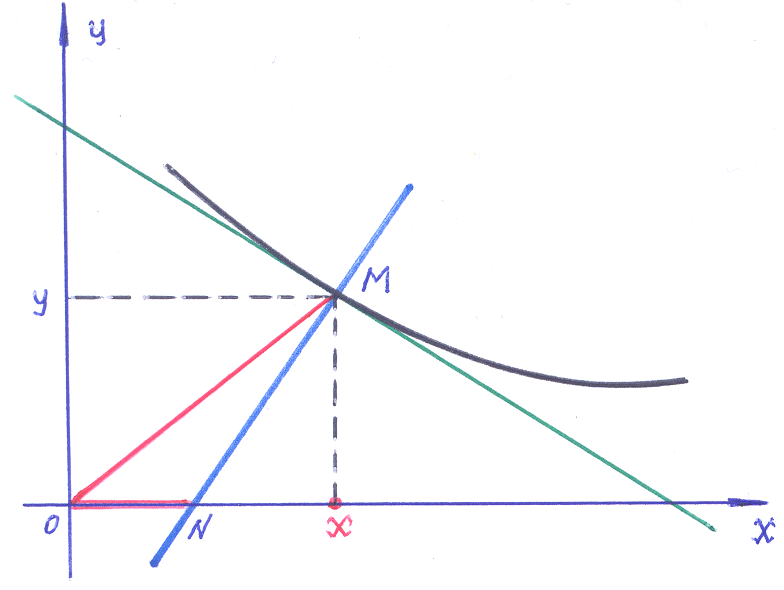 ешение:

Замечание: 1). При составлении дифференциального уравнения необходимо учесть возможные варианты названного в условии равенства: 2|OM|² = |x∙ON|.

2). Для лучшего восприятия задачи воспользуемся рисунком: отрезки ОМ, ОN и абсцисса точки М выделены красным цветом.

Итак, через некоторую точку М(x,y) плоскости OXY проходит кривая y=(y) со свойством:

▪ Случай-1: 2(x²+y²)= x∙(x+yy′); (1)

▪ Случай-2: 2(x²+y²)=–x∙(x+yy′). (2)

Случай-1.

1). Из условия запишем: y′ = = +2 – однородное дифференциальное уравнение для нахождения кривой с заданными свойствами. Остается решить это уравнение!

2). Применим стандартный алгоритм решения задачи:

a¹. Исходная запись ДУ решений не дает.

a². Примем = u; получим: φ(u)=f(u)–u= +2u–u= +u= .

a³. Проверим условие: φ(u₀)= f(u₀)–u₀=0. Дополнительных решений не получим.

a⁴. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде (1): 2 =2 . (3)

a⁵. Интегрируем уравнение (3): ln(u²+1)= lnCx² → u²+1=Cx².

a⁶. Записываем общее решение ДУ. Учитывая что , получаем: y²=x²(Cx²–1).

a⁷. Записываем частное решение ДУ, учитывая что интегральная кривая должна пройти через точку (1,2) → С=5 : получаем: y²=x²(5x²–1).

Случай-2.

1). Из условия запишем: y′ =– =–3 –2 – однородное дифференциальное уравнение для нахождения кривой с заданными свойствами. Остается решить это уравнение!

2). Применим стандартный алгоритм решения задачи:

a¹. Исходная запись ДУ решений не дает.

a². Примем = u; получим: φ(u)=f(u)–u= +2u–u=–3 –3u=–3 .

a³. Проверим условие: φ(u₀)= f(u₀)–u₀=0. Дополнительных решений не получим.

a⁴. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде (1): –6 =2 . (3)

a⁵. Интегрируем уравнение (3): –3ln(u²+1)= lnCx² → u²+1=C .

a⁶. Записываем общее решение ДУ. Учитывая что , получаем: y²=x²(C –1).

a⁷. Записываем частное решение ДУ, учитывая что интегральная кривая должна пройти через точку (1,2) → С=5 : получаем: y²=x²(5 –1).

Ответ: Случай-1: y²=x²(Cx²–1).– общее решение ДУ, частное решение: y²=x²(5x²–1).

Случай-2: y²=x²(C –1).– общее решение ДУ, частное решение: y²=x²(5 –1)

Замечание: задачние «зевнул» второе решение!

Пример 8–188: Через сколько времени температура тела, нагретого до 100⁰С, понизится до 25⁰С, если температура помещения равна 20⁰С и за первые 10 мин тело охладилось до 60⁰С?

Решение:

Замечание: задача интересна «физической стороной» вопроса: физик использует общее решение для определения характеристик остывания конкретного тела в заданных условиях! Общее решение задачи нами получено в Примере 8–187: T=a+(Т₀–a)e^–kt. (2)

1). Из условия задачи следует: Т₀–a=80⁰С, Т–a=40⁰С, t=10 мин.

2). Из уравнения (1) следует: (e^–k)¹⁰ =0.5 → (e^–k)= .

3). Теперь имеем: Т–a=75⁰С =( )^t, или ( )^t = → t ≈40 мин.

Ответ: t ≈ 40 мин.

☻

Вопросы для самопроверки:

1. Как определяют ДУ в полных дифференциалах?

2. Как определить, что данное уравнение есть ДУ в полных дифференциалах?

3. Каков «стандартный алгоритм» решения ДУ в полных дифференциалах?

4. Что такое «интегрирующий множитель уравнения»?

5. Привести пример применения ДУ для решения задачи из геометрии.

6. Привести пример применения ДУ для решения задачи из физики.

< * * * * * >