2). Далее решаем уравнение, применяя общий алгоритм:

a⁰. Находим первообразную функции М = :

u(x,y)= + φ(y)= +φ(y)= x²+x∙lny+φ(y). (1)

a¹. Подберем φ(y) так, чтобы выполнялось условие: = N(x,y); это значит, что выполняется: ( x²+x∙lny)+φ′(y)= +φ′(y)=N(x,y); (2)

a². Используя (2), запишем равенство для вычисления функции φ′(y):

φ′(y)= N(x,y)– =siny. (3)

a³. Интегрируем (3) и окончательно «восстанавливаем» функцию u(x,y):

φ(y)= = –cosy. (4)

a⁴. Запишем общее решение заданного уравнения:

u(x,y)= + =x²+x∙lny–cosy= С. (5)

Ответ: u(x,y)=x²+x∙lny–cosy= С – общее решение.

Пример 8–171: Найти уравнение кривой, проходящей через точку , если для любого отрезка [1,x] площадь криволинейной трапеции, ограниченной соответствующей дугой этой кривой, на 2 больше отношения абсциссы x концевой точки к ординате y.

Решение:

З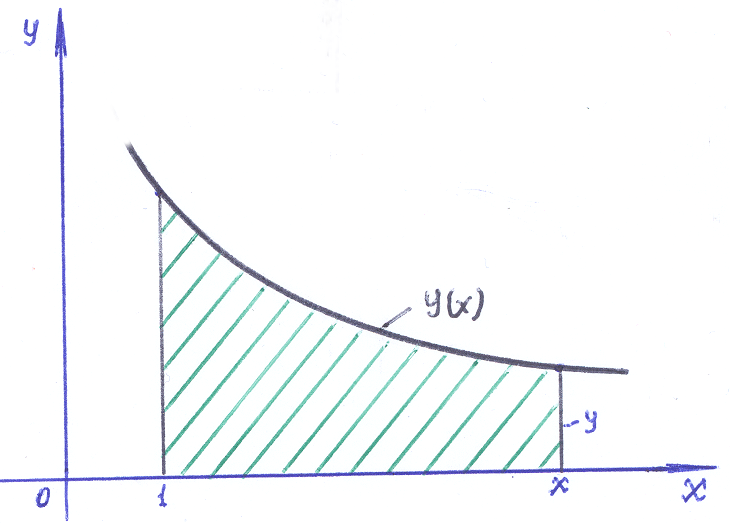 амечание: а). При решении задачи используется производная интеграла по верхнему «переменному пределу»;

б). Необходимо отметить «безразличие» решения к «числу 2».

1) Составим «интегральное» уравнение:

= +2. (1)

2). Дифференцируя (1), получаем дифференциальное уравнение:

y= – x y′, или y′– y=– y³. (2)

3). Уравнение (2) – уравнение Бернулли для n=3. Алгоритм решения стандартный:

a⁰. Примем: z = y^–n+1, где (–n+1)= –2; то есть: z=y^–2.

a¹. Запишем преобразованное уравнение Бернулли: z′+2 z=2 . (3)

a². Решение уравнения ищем в виде: функцию z=u(x)∙v(x);

a³. Вычислим интеграл: – =–2 =–lnx² → u= = .

a⁴. Вычислим функцию v: v = = 2 +С= x² +С;

a⁵. Запишем общее решение уравнения для (3): z=u∙v= ∙( x² +С). (4)

a⁶. Учитывая: z=y^–2, запишем общее решение для (1): y^–2= ∙( x² +С), или (удобнее для использования): y²= .

a⁷. Учитывая начальные условия, запишем частное решение: .

Ответ: y²= – общее решение уравнения. Частное решение: .

Замечание: решение y=0 в нашем случае «геометрически неинтересное», потому в ответе не отмечено.

Пример 8–187: Скорость охлаждения тела пропорциональна разности температур тела и окружающей среды (закон Ньютона). Найти зависимость температуры Т от времени t, если тело, нагретое до Т₀ градусов, внесено в помещение, температура которого постоянна и равна а градусам.

Р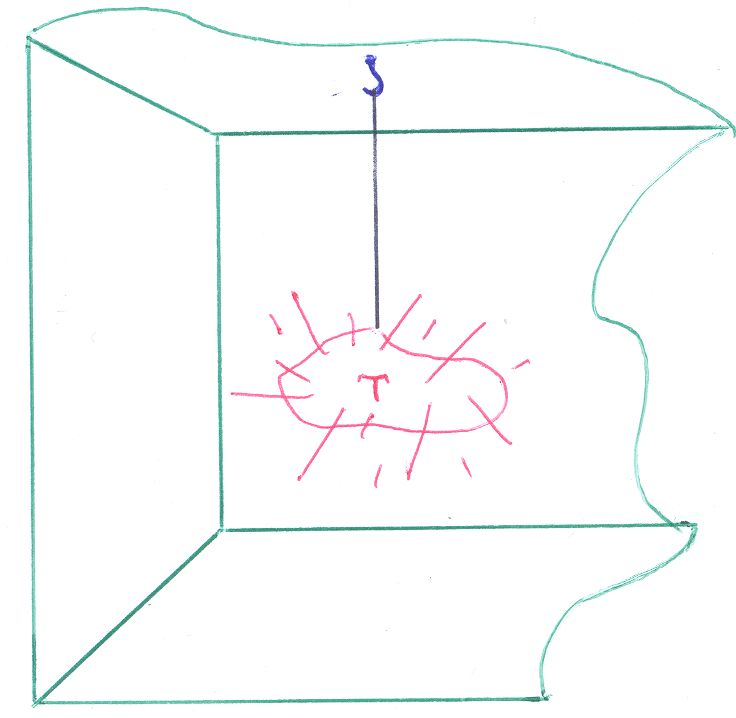 ешение:

Замечание: рисунок «мотивирует» решение задачи, а также «намекает», что охлаждение тела происходит за счет «молекулярного взаимодействия» тела и среды: подвеска тела к потолку на тонкой нити с минимальной теплопроводностью.

1). Из условия задачи следует дифференциальное уравнение:

=–k(T–a). (1)

2). Уравнение (1) – ДУ с разделяющимися переменными. Его стандартная форма записи:

=–kdt. (2)

3). В результате интегрирования уравнения (2) получаем общее решение задачи:

T=a+Ce^–kt. (3)

4). Учитывая начальные условия, получаем частное решение задачи:

T=a+(Т₀–a)e^–kt. (4)

Ответ: T=a+Ce^–kt – общее решение уравнения. Частное решение: T=a+(Т₀–a)e^–kt.

* * * * * * * * * *

Домашнее задание

Дома

Л-3

гл.10: № 97, 99,101,103,105,143,181,188.

8

Пример 1–97: Решить дифференциальное уравнение: (10xy–8y+1)dx+(5x²–8x+3)dy=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.

Решение:

1). В нашем случае: =10x–8 и =10x–8 → условие = выполняется → задано уравнение в полных дифференциалах.