Тема 1. Множества, отношения, функции.
1.1 Элементы и множества
Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. Можно сказать, что множество — это любая определенная совокупность объектов. Объекты, из которых составлено множество – называются его элементами. Элементы множества различны и отличимые друг от друга.
Пример.
Множество S страниц в данной книге. Множество N натуральных чисел 1, 2, 3, ,… Множество Р простых чисел 2, 3, 5, 7, 11, ... Множество Z целых чисел: ... , -2, -1, 0, 1, 2, ... Множество R вещественных чисел. Множество А различных символов на этой странице.
Если объект x
является
элементом множества М,
то говорят, что х
принадлежит М,
Обозначение:
.
В противном случае говорят, что х
не принадлежит М.
Обозначение:
.
Обычно множества обозначают прописными буквами латинского алфавита, а элементы множества — строчными буквами.
Множества, как объекты, могут быть элементами других множеств. Множество, элементами которого являются множества, обычно называется классом или семейством. Множество, не содержащее алиментов, называется пустым. Обозначение:Ошибка! Объект не может быть создан из кодов полей редактирования..
Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества U (своего для каждого случая), которое называется универсальным множеством (или универсимом).
1.2 Задание множеств
Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:
а)
перечислением элементов: 
б)
характеристическим
предикатом: 
в)
порождающей процедурой: 
Примеры:
а)
б)
в)
{n
|
for
n
from
1
to 9 yield
n
}.
1.3 Операции над множествами
Самого по себе понятия множества еще недостаточно — нужно определить способы конструирования новых множеств из уже имеющихся, то есть операции над множествами.
Сравнение множеств. Множество А содержится в множестве В (множество В включает множество А), если каждый элемент А есть элемент В:
В этом случае А называется подмножеством В, В – надмножеством А.
Если
и
,
то А
называется собственным
подмножеством В.
Заметим, что
.
По
определению
.
Два множества равны, если они являются подмножествами друг друга:
.
Мощность
множества М
обозначается
как |М|.
Для конечных множеств мощность — это
число элементов. Например, |
|
= 0, но |{
}|
= 1. Если |A|
= |В|, то множества А и В называются
равномощными.
Обычно рассматриваются следующие операции над множествами:
а) объединение:
б) пересечение:
в) разность:
г) симметрическая разность:
д) дополнение:
Операция дополнения
подразумевает некоторый
универсум
.
Пример.
Пусть А : ={1,2,3}, В :={3,4,5}.
Тогда:
На рис 1.1 приведены диаграммы Венна, иллюстрирующие операции над множествами. Сами исходные множества изображаются фигурами (в данном случае овалами), а результат графически выделяется (в данном случае для выделения использована штриховка).
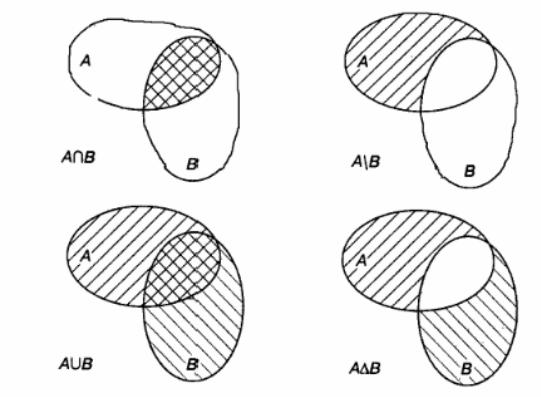
Рис. 1.1. Операции над множествами