1. Сигналы

Сигналом называется электрическое, электромагнитное, акустическое или другое колебание, несущее информацию. Электроника имеет дело с электрическими, электромагнитными и акустическими сигналами.

Сигналы подразделяются на детерминированные и случайные. Детерминированным сигналом называется колебание (несущее информацию), которое может быть описано некоторой аналитической функцией, т.е. формулой. В этом случае информация заложена либо в самом факте появления сигнала, либо во времени его прихода. К случайным сигналам относятся колебания (несущие информацию), которые нельзя описать аналитической функцией, а для их описания требуется аппарат теории вероятностей.

1. 1. Детерминированные сигналы

Детерминированные сигналы подразделяются на периодические и непериодические. К периодическим сигналам относятся сигналы, значение которых повторяется через некоторый фиксированный интервал времени. Минимальный интервал времени, через который сигнал повторяет свое значение, называется периодом периодического сигнала.

Для непериодического сигнала не существует интервала времени, через который сигнал повторяет свое значение.

Периодический сигнал описывается функцией, для которой выполняется условие:

s(t) = s(t + nT), (1.1.1)

где

n – любое целое число, как положительное, так и отрицательное;

T – период сигнала.

Пример периодического сигнала приведен на рис.1.1.

s(t)

Е

t

τ 0

T

Рис. 1.1. Последовательность прямоугольных импульсов длительностью τ и периодом Т.

Простейшим периодическим сигналом является гармонический сигнал, который описывается функцией вида:

s(t) = A Cos (ωt + φ ), (1.1.2)

где А – амплитуда гармонического сигнала, ω - частота гармонического сигнала (измеряется в рад/сек), φ – начальная фаза гармонического сигнала, ω = 2 π f, f – циклическая частота (измеряется в Гц или в 1/сек).

- 2 -

Важнейшим свойством гармонического сигнала является то, что при прохождении через линейные электронные средства этот сигнал не меняет своей формы, а изменяет только амплитуду и начальную фазу. Это свойство позволяет использовать гармонические колебания при анализе линейных цепей.

Из математики известно, что

exp (jα) = Сos α + j Sin α, (1.1.3)

Тогда

s(t) = Re A exp (ωt+φ) (1.1.4)

или

s(t) = Re A exp (φ) exp (ωt) = Re à exp (ωt), (1.1.5)

где

à = A exp (φ) – комплексная амплитуда гармонического колебания.

Комплексной амплитудой гармонического колебания называется такое комплексное число, модуль которого равен действительной амплитуде гармонического колебания, а аргумент – начальной фазе гармонического колебания.

1.2. Спектры периодических сигналов

Р ассмотрим произвольный периодический сигнал с периодом Т (рис.1.2).

s(t)

t

0

T

Рис. 1.2. Произвольный периодический сигнал с периодом Т.

Из математики известно, что на интервале Т сигнал можно представить в виде набора гармонических колебаний вида (разложение в ряд Фурье):

∞

s(t) = ao/2 + ∑ [an Cos(nΩt) + bn Sin(nΩt)], (1.2.1)

n=1

где ao/2, an, bn – коэффициенты ряда Фурье, которые связаны с сигналом s(t) следующими выражениями:

T/2 T/2 T/2

ao/2=(1/T)∫s(t) dt, an=(2/T)∫s(t)Cos(nΩt)dt, bn=(2/T)∫s(t)Sin(nΩt)dt,

` -T/2 -T/2 -T/2 (1.2.2)

- 3 -

где Ω = 2π/T – основная частота периодического сигнала или частота первой гармоники сигнала, частоты ωn = nΩ называются частотами высших гармоник сигнала.

Выражение (1.2.1) можно переписать в виде:

∞

s(t) = ao/2 + ∑An Cos (nΩt + φn), (1.2.3)

n=1

где

An=√(an)² + (bn)² - действительная амплитуда n-ой гармоники сигнала,

φn = - arctg(bn/an) начальная фаза n – ой гармоники сигнала.

Выражение (1.2.3) называется рядом Фурье в тригонометрической форме.

Величина ао /2 называется постоянной составляющей сигнала или его средним значением.

Совокупность амплитуд (An) гармонических составляющих сигнала и ао/2 называется амплитудным спектром периодического сигнала или его амплитудно-частотной характеристикой (АЧХ).

Совокупность начальных фаз (φn) гармонических составляющих сигнала называется фазовым спектром периодического сигнала или его фазочастотной характеристикой (ФЧХ).

Совокупность амплитуд (An), (φn) и ао /2 полностью определяют периодический сигнал.

Выражение (1.2.3) можно представить в комплексном виде

∞

s(t) = 0,5 ∑Ãn exp(jnΩt), (1.2.4)

n═ - ∞

T/2

где Ãn = =(2/T)∫s(t)exp(-jnΩt)dt.

-T/2

Учитывая, что An - четная, а φn - нечетная функции частоты, и используя формулы Эйлера уравнение 1.2.4 легко переходит в уравнение 1.2.3.

Пример.

Дана периодическая последовательность прямоугольных импульсов (рис.1.3).

s(t)

Е

-τ /2 τ /2 t

T

Рис. 1.3. Последовательность прямоугольных импульсов длительностью τ и периодом Т.

• 4 –

Найти: амплитудный An и фазовый спектр φn заданного сигнала.

На интервале периода сигнал может быть записан в виде:

Е , -τ /2 ≤ t ≤ τ /2 ,

s(t) = (1.2.5)

0, τ/2 ≤ t ≤ (T – τ/2).

Найдем постоянную составляющую:

τ/2 τ/2

ао /2 = (1/T) ∫E dt = Et/T = E τ/T.

- τ/2 -τ/2

Найдем коэффициенты ряда Фурье аn и bn:

τ/2 τ/2 4E Sin(nΩt) τ/2

a n =(2/T)∫s(t)Cos(nΩt)dt = (4/T) )∫s(t)Cos(nΩt)dt = =

-τ/2 0 nΩ 0

Sin(nΩτ/2)

= (2E τ/T) .

nΩτ/2

bn = 0, так как подинтегральная функция нечетная.

Поэтому

Sin(nΩτ/2)

A n = an = (2E τ/T) ,

nΩτ/2

0, если an > 0;

φn =

π, если an < 0.

Графики Аn и φn приведены на рис.1.4, а и б.

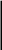
Аn а) φn б) nΩ

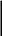
nΩ -π

1.4. Амплитудный (а) и фазовый (б) спектры рассматриваемого сигнала.

Как видно из рис. 1.4 спектры периодических сигналов имеют линейчатый характер.