2.6. Построение зависимостей спроса от предложения

Рассмотрим зависимость спроса от предложения. Кривые спро­са и предложения D = D(P) и S(P) = S запишем в виде

D=f(S).

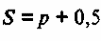Из и имеем

это кривая 1 на рис. 3.6.

Кривая 2 из уравнений и определяется как

Из уравнений находим уравнение кри­вой 3

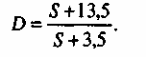
Уравнение кривой 4:

найдено из уравнении

Проведем биссектрису первого координатного угла, которая пересекает кривые D = f(S) в точках, соответствующим равновес­ным ценам. Выше биссектрисы D > S, что отвечает зоне отсутствия риска. Ниже биссектрисы D < S — это зона повышенного риска. Таким образом, зоне повышенного риска отвечает нера­венство f(S) - S < 0, а зоне отсутствия соответствует неравенство f(S) - S > 0.

Полученные результаты можно использовать для разработки методов внерыночного регулирования, основанных на субсидиях и дотациях. В некоторых случаях существование равновесия не является само собой разумеющимся и его реализация требует до­полнительных усилий:

ситуация, в которой производитель несет большие издерж­ки в процессе производства и поэтому не может начать постав­лять продукцию по цене ниже обусловленной границы рентабель­ности (Рр). Однако эта цена оказывается весьма высокой для потребителей и спрос при ценах оказывается меньше объемов производства, при которых оно рентабельно.

В этой обстановке равновесия в узком смысле не существует, но есть равновесие в широком смысле при 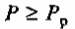(предложение больше спроса). Положение может быть исправлено путем доти­рования производителя, после чего кривая предложения {S₂) пе­ремещается в положение (S₃) (рис. 3.5) и может быть достигнута точка равновесия;

случай дефицита, когда производство товара невелико и сла­бо реагирует на повышение цены, т.е. почти или полностью не­эластично, а потребители готовы приобрести большое количество товара практически по любой цене.

Нетрудно видеть, что в области разумных цен нет равновесия ни в узком, ни в широком смысле, напротив, имеет место дефицит товара. Равновесие может быть достигнуто либо путем резкого подъема производства, либо посредством резкого ограничения доходов потребителей, например денежной реформы.

3.Влияние фактора времени на степень риска

Рисковый поток — часть единого временного потока. Вре­мя — основной человеческий ресурс. Человек приходит в эту жизнь с определенным запасом времени, в течение которого у него есть возможность создать себе подобных, обогатить (развить) свое со­знание, осознать переходящий характер земной действительнос­ти и захотеть устремиться в беспредельность, чтобы понять отно­сительность ограниченности всех видов ресурсов, в том числе и времени.

Необходимо тщательно выбрать момент, с которого начина­ется процесс принятия и реализации управленческого решения в ситуации риска, так как начальное состояние значительно, как правило, отличается от того, которое было во время подготовки и выработки решения. Существующая зависимость между време­нем, которое имеет в распоряжении управленческий персонал и риском, требует от менеджеров, предпринимателей держать этот аспект управленческой деятельности под постоянным контролем. И если, в процессе управленческих воздействий на объект в ситу­ации риска, удалось прийти к разрешению неопределенности, то опоздание в реализации снова приведет к нарастанию неопреде­ленности в деятельности фирмы, компании. Все это можно гра­фически изобразить следующим образом (рис 3.7).

Учет фактора времени при экономических расчетах обуслов­лен тем, что при оценке экономической эффективности принима­емых решений как эффект, так и затраты могут быть распределе­ны во времени. Так при создании сложных объектов (промыш­ленные предприятия, гидросооружения, прокладка газопроводов и др.) их проектирование и строительство ведется несколько лет. При этом точное определение затрат и получаемых полезных ре­зультатов в течении нескольких лет практически невозможно.

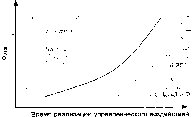
Рис. 3.7. График зависимости между временем и риском

В данной ситуации возникает необходимость учета фактора време­ни при определении капитальных вложений и расходов, связан­ных с проектированием, созданием и эксплуатацией новой техни­ки и прогрессивных технологий.

С учетом фактора времени можно решать следующие задачи:

прогнозирование затрат и результатов;

определение распределенных во времени затрат и резуль­татов в любой момент времени;

определение коэффициента дисконтирования (нормы доход­ности, процентной ставки) при известных начальных и будущих затратах и результатах.

Влияние фактора времени следует учитывать, исходя из двух точек зрения:

из-за наличия инфляционных процессов, связанных с обес­цениванием денег, необходимо учитывать покупательную способ­ность денег, которая является различной в различные моменты времени при равной номинальной стоимости;

из-за обращения денежных средств в виде капитала и полу­чения дохода с оборота, ибо один и тот же капитал имеющий боль­шую скорость оборота, обеспечит большую величину дохода.

Для определения будущих доходов или затрат применяется формула наращения сложных процентов:

(3.3.1)

где Р — начальная оценка вложения,

i — коэффициент дисконтирования (процентная ставка, норма доход­ности),

Рt — вложения к концу t — го периода времени с момента вклада пер- . вон анальной суммы.

Пример 3.1. Годовая ставка сложных процентов равна 15%. Через сколько лет начальная сумма утроится?

Введение 2

1. Факторы ограничения риска 3

2. ВЛИЯНИЕ ФАКТОРОВ РЫНОЧНОГО РАВНОВЕСИЯ НА ИЗМЕНЕНИЕ РИСКА 6

2.1.Взаимосвязь рыночного равновесия и коммерческого риска 6

2.2. Влияние факторов рыночного равновесия на изменение коммерческого риска 7

2.3. Моделирование процесса достижения равновесия 9

2.4. Влияние изменения спроса на уровень коммерческого риска 13

2.5.Влияние изменения предложения на степень коммерческого риска 15

2.6. Построение зависимостей спроса от предложения 16

3.ВЛИЯНИЕ ФАКТОРА ВРЕМЕНИ НА СТЕПЕНЬ РИСКА 18

4.Влияние факторов эластичности предложения и спроса на уровень риска 25

5. ВЛИЯНИЕ ФАКТОРА НАЛОГООБЛОЖЕНИЯ В РЫНОЧНОМ РАВНОВЕСИИ НА УРОВЕНЬ РИСКА 35

Отсюда следует, что сумма утроится через восемь лет.

Пример 3.2. Какая ситуация выгоднее: взять сегодня $2000 или $4000 через восемь лет при ставке 6%.

Найдем современную начальную величину Р из формулы (3.3.1):

Следовательно, выгоднее взять $4000 через восемь лет.

Пример 3.3. Срок разработки проекта составляет три года. Ка­питальные вложения в начале каждого года составляют величи­ны К₁ =2 млн руб., К2- 4 млн. руб., K₃ = 3 млн руб. Коэффициент дисконтирования i= 60%. Необходимо определить суммарные капитальные вложения к концу срока разработки.

Капитальные вложения первого года к концу срока разра­ботки:

Капитальные вложения второго года к концу срока разработки:

Капитальные вложения третьего года к концу срока разработки:

Суммарные капитальные вложения, определенные с учетом фактора времени:

Пример 3.4. Инвестор располагает 5 млн руб. и хочет полу­чить через три года 20 млн руб. Следует определить, под какую процентную ставку ему следует отдавать эти деньги.

Из соотношения записанной на основании фор­мулы (3.3.1), получаем i = 0,59. Таким образом, необходимо вло­жить капитал в такие мероприятия, которые обеспечат годовой доход в размере не ниже 59%.

Фактор времени усиливает действие фактора неопределенно­сти. В общем случае при определении полезных результатов и зат­рат, зависящих от времени, основные виды неопределенности ха­рактеризуются следующими причинами:

быстрым изменением внешней среды (экономической, тех­нологической, политической и т.п.) во времени;

отсутствием сведений о состоянии внешней среды в различ­ные моменты времени;

недостаточной информацией о функционировании анализи­руемых систем в будущем;

отсутствием единого мнения участников выполнения проек­тов на отдельных этапах времени;

наличием конфликтных ситуаций, возникающих среди учас­тников проекта;

возникновением антагонизма между участниками проекта и внешней средой.

В этом параграфе был рассмотрен пример, в котором пред­полагалось, что капитальные вложения в различные годы изве­стны точно. В реальных задачах данное условие, как правило, не выполняется. Указанные капитальные затраты зависят от множества факторов, среди которых имеются факторы неопре­деленности, т е. те, которые являются непредсказуемыми. По­этому в общем случае определяемые капитальные вложения являются функцией указанных неопределенных факторов, т.е. где

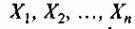— определенные факторы, — неопре­деленные факторы. В качестве Yt могут быть: состояние фирмы, рыночная конъюнктура, условия строительства объекта, погод­ные условия и т.п.

Для оценки характеристик инвестиционных проектов важ­нейшее значение имеет ставка дисконтирования будущих дохо­дов к современному моменту. Если будущие платежи рискован­ны, т.е. не являются жестко определенными, то инвесторы умень­шают сегодняшнюю оценку будущих доходов. Тем самым для оценки сегодняшнего значения будущих доходов приходит­ся применять увеличенную ставку дисконтирования. Самое про­стое — расклассифицировать проекты на низкорискованные, среднерискованные и высокорискованные и приписать каждой группе некоторый добавок к обычному коэффициенту дискон­тирования. Например, для низкорискованных к ставке прибавляется 2%, к среднерискованным — 4%, к высокорискован­ным — 6%. Совершенно ясно, что «добавок» зависит от величи­ны обычного коэффициента дисконтирования, но сам этот коэф­фициент зависит от темпов инфляции, от доверия к политике государства и других факторов.

Отсюда можно сделать вывод: чтобы увеличить привлекатель­ность выдвигаемых проектов, фирма должна заботиться об умень­шении этого рискового «добавка». Для этого она должна привле­кать к себе доверие потенциальных инвесторов. Привлечение до­верия включает своевременную выплату дивидендов, соблюдение прав акционеров и др. Особенно это важно для фирмы, намерива­ющейся долго работать. Такой фирме просто необходимо быть честной.

Пример 3.5. Проанализировать инвестиционный проект (-1000, 600, 600), процентная ставка 8%. Окупаются ли инвестиции? Эксперты признали проект среднерисковым и увеличили процент дисконтирования будущих доходов до 13%. Окупаются ли инвес­тиции в этом случае?

Данный инвестиционный проект означает, что в начальный момент вложены инвестиции размером Inv - 1000, а затем, напри­мер, в течении 2 лет получены доходы = 600, D2 = 600. Ставка процента 8% в год.

Наверху указаны размеры инвестиций (отрицательные) и по­лученные доходы (положительные). Допустим, доходы вклады­ваются в тот же банк, который и дал инвестиции и на доход на­числяются те же сложные проценты, под которые банк выдал кре­дит — инвестиции. Верхняя строка под линией — размер счета в банке до внесения очередного платежа дохода. Средняя строка — этот самый платеж доход, ниже — итоговый размер счета в банке. Итак, (-1080) — это наращенная за один год сумма выданных в кредит инвестиций, добавляем доход 600, получим (-480) — долг заемщика банку. В конце второго года этот долг заемщика увели­чивается на 8% и становится равным (-518,4), добавляем доход 600 и получаем 81,6. Это означает, что к концу второго года инве­стиции окупились и наращенная величина чистого дохода равна 81,6. Если эту величину дисконтировать к моменту 0 по ставке 8%, то получим

Эта величина называется приведенным чистым доходом проекта. Если ее поделить на абсолютную величину инвестиций, то полу­чим доходность проекта (иногда эту величину называют рентабельностью проекта): , или 7%.

Проведем аналогичные расчеты для процентной ставки 13%.

Отсюда видно, что инвестиции к концу второго года не оку­пятся, т.е. проект является нерентабельным.

Рассмотрим далее случайные рисковые потоки платежей час­то встречающиеся на практике.

Пусть единичные платежи следуют друг за другом через случайные промежутки времени, распределенные по показатель­ному закону с параметром λ > 0 (пуассоновский поток плате­жей), дифференциальная функция распределения которого имеет вид:

(3.3.2)

где Т — среднее время между платежами. Найдем современ­ную величину такого случайного потока платежей (математическое ожидание этой величины).

Дисконтируем к современному моменту первый платеж. Из формулы (3.3.1) имеем Умножаем равенство на и интегрируем по t:

Введение 2

1. Факторы ограничения риска 3

2. ВЛИЯНИЕ ФАКТОРОВ РЫНОЧНОГО РАВНОВЕСИЯ НА ИЗМЕНЕНИЕ РИСКА 6

2.1.Взаимосвязь рыночного равновесия и коммерческого риска 6

2.2. Влияние факторов рыночного равновесия на изменение коммерческого риска 7

2.3. Моделирование процесса достижения равновесия 9

2.4. Влияние изменения спроса на уровень коммерческого риска 13

2.5.Влияние изменения предложения на степень коммерческого риска 15

2.6. Построение зависимостей спроса от предложения 16

3.ВЛИЯНИЕ ФАКТОРА ВРЕМЕНИ НА СТЕПЕНЬ РИСКА 18

4.Влияние факторов эластичности предложения и спроса на уровень риска 25

5. ВЛИЯНИЕ ФАКТОРА НАЛОГООБЛОЖЕНИЯ В РЫНОЧНОМ РАВНОВЕСИИ НА УРОВЕНЬ РИСКА 35

и конечные результаты подставляем в соотношение (3.3.3)

или, деля числитель и знаменатель на , получаем

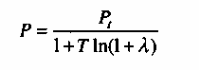
Следовательно, учитывая, что 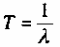есть среднее время между платежами, математическое ожидание современной величины первого платежа равно

Так как промежуток времени между платежами распределен одинаково, то математическое ожидание современной величины второго платежа равно

и т.д. Сумма всех этих величин, представляющая сумму членов бесконечно убывающей геометрической прогрессии со знаменателем , равна

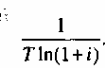
Таким образом, среднее значение суммы всех платежей

равно

В частности, при Т = 1 имеем 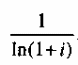. Отметим, что если бы поток был неслучайным и платежи следовали бы друг за другом через единичный промежуток времени (тогда частота платежей была бы той же самой), то современная величина такого потока была бы - и, так как то современная величина случайной ренты больше, чем регулярной.

Потоки платежей со случайным временем платежа встречаются на практике часто. К ним можно отнести поток платежей оплаты за телефон, поток выплат страховых сумм за пострадавший в ава­рии автомобиль и т.п.