Тема №4 Применение производной в экономической теории
Типовые примеры
Задание 1
Вычислить предел
;
Решение
Подстановка предельного значения
переменной x в выражение,
стоящее под знаком предела приводит к
неопределенности
.
Для устранения этой неопределенности числитель и знаменатель дроби разложим на множители и сократим дробь на общий множитель.
Задание 1
Вычислить предел
Числитель и знаменатель дроби стремятся
к бесконечности (неопределенность
вида
).
Для устранения этой неопределенности числитель и знаменатель дроби делим почленно на старшую степень переменной x в данной дроби, т.е. на x3.
.
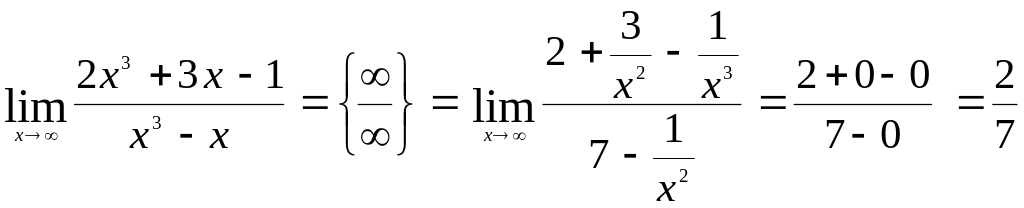Задание 1
Вычислить предел
Решение
Подстановка предельного значения
переменной x в выражение
, стоящее под знаком предела, приводит
к неопределенности
.Для
устранения неопределенности в числитле
дроби следует избавиться от рациональности
умножением числителя и знаменателя на
сопряженное выражение
, а знаменатель разложить на множители.
Задание № 2
Найти производную Функции
y=
Решение:
Воспользуемся известным правилом
дифференцирования суммы и разности
функций
и теоремой о производной сложной
функции
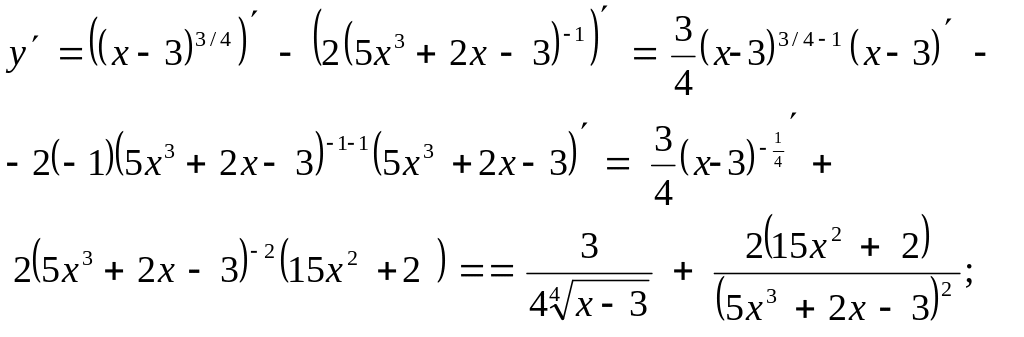
Задание 2
Найти производную функции
Решение
Воспользуемся правилом дифференцирования произведения двух функций
и формулами
Задание 2
Найти производную функции
Решение
Воспользуемся следующими формулами дифференцирования:
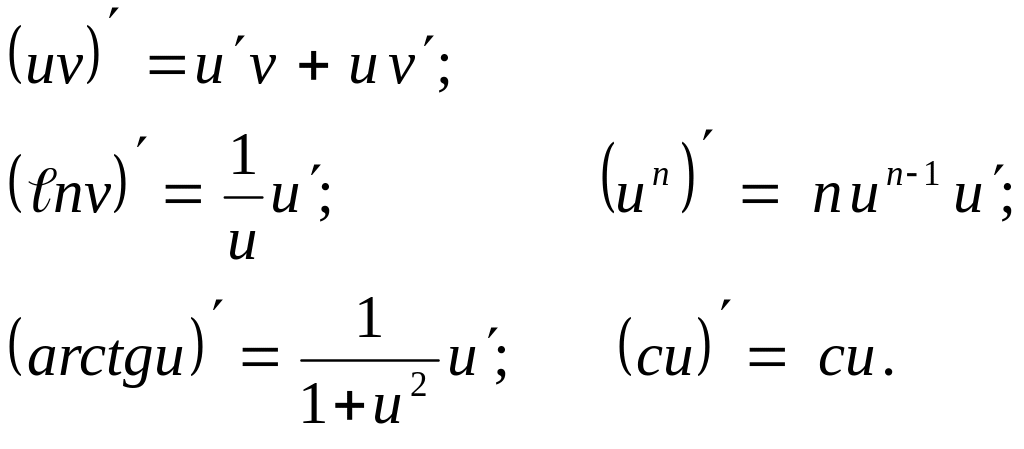
Задание 3
Провести полное исследование функции
и построить ее график.
Решение:
1. Область определения функции
т.е.
вся числовая прямая, кроме точки x
= 0, где знаменатель обращается в нуль
2.Функция не является ни четной, ни нечетной, т.к. не выполняется ни одно из условий
В самом деле
полученное выражение не равно ни
,ни
Т. о. график функции не является симметричной кривой.
Функция не является периодической
3. Функция непрерывна всюду, кроме точки
(как
элементарная
функция)
,
т.е. прямая
является вертикальной асимптотой.
4.Точек пересечения с осью ординат график
функции не имеет, т. к.
.
Для определения точек пересечения с
осью абсцисс решим уравнение
;
т.к.
то
,
т.е. график функции пересекает ось
абсцисс в точке
.
5.Для определения точек экстремума, интервалов монотонности функции найдем первую производную
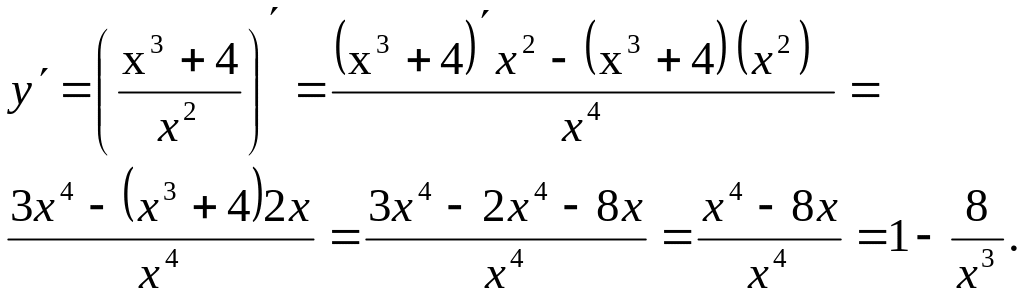
Приравняем производную к нулю и найдем
критические точки
При производная не существует ,но эта точка не является критической, т .к. в ней не существует и сама функция.
Критическая точка разбивает всю область
определения функции на следующие
интервалы
.
Заполним следующую таблицу
|
|
|
|
|
|
|
- |
не сущ. |
- |
0 |
+ |
|
|
не сущ. |
|
min |
|
Найдем
Функция имеет минимум в точке
6.
Для
определения интервалов выпуклости,
вогнутости, точек перегиба найдем вторую
производную
;
Вторая производная
в области определения функции положительна,
поэтому график всюду вогнут, точек
перегиба нет.
7 Найдем наклонные асимптоты кривой,
которые имеют уравнение
Т.о. наклонная асимптота кривой имеет
уравнение
.
8.Строим график функции. Сначала на координатной плоскости строим асимптоты и ;затем характерные точки.
Y
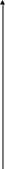
y=x
(2,3)
X
Задание 4
Вычислить приближенно с помощью
дифференциала
;
Решение:
Если
получает некоторое приращение
,
то соответствующее приращение функции
можно
представить в виде
где
есть бесконечно малая величина высшего
порядка относительно
В приближенных вычислениях принимают
или
,
откуда
Обозначая
через
,
получаем формулу приближенного вычисления
Следует учесть, что значение
нужно представить в виде
.
таким образом , чтобы значение
было известно или легко вычислялось, а
величина приращения
была
по возможности наименьшей.
Итак
и требуется найти
.
Число 1000 можно представить в виде
так, чтобы
,
а также
легко вычислялось, и кроме того,
было
по возможности минимальным. Так как
и
,
то целесообразно взять
.
Тогда
,
откуда
.
В сравнении с заданным числом
величина
является
небольшой, поэтому можно воспользоваться
формулой (1).Для этого вычислим
.
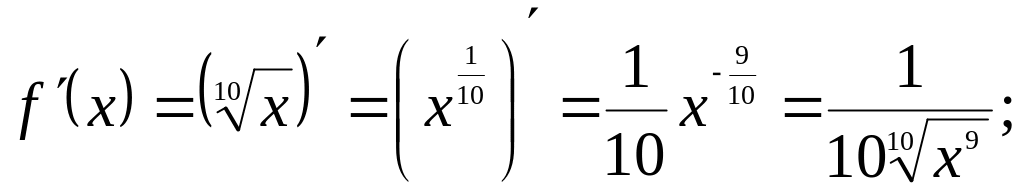
Тогда
.
Задание 8.
Найти частные производные и частные
дифференциалы функции z=ctg
Решение.
Найдём частные производные:
;
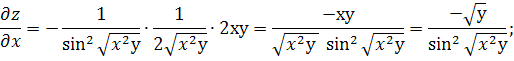
Найдём частные дифференциалы.
dz
=
dz
Задание 9
Исследовать на экстремум функцию z=
Решение.
Найдём частные производные:
Используя необходимое условие экстремума:
Составим систему уравнений
Решив эту систему найдём четыре стационарные точки.
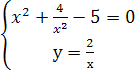
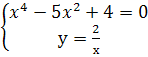
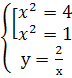
Стационарные точки М
(-2;-1);
М
(2;1);
М
(-1;-2);
М
(1;2)
Найдём производные второго порядка
=6у;
И составим дискриминант ∆=А
для каждой стационарной точки
Для точки М : А=
;
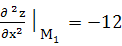В=
;
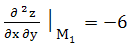С=
∆=А
.
В точке М
функция имеет максимум, равный
z
=-8-6+30+12=28
Для точки М : А=12; В=6; С=12;
∆=144-36>0; А>0.
В точке М
функция имеет минимум, равный
z
=8+6-30-12=-28
Для точки М : А=-6; В=-12; С=-6;
∆=36-144<0. Экстремума нет
Для точки М : А=6; В=12; С=6;
∆=36-144<0. Экстремума нет
Расчетные задания.
Задание1
Вычислить предел:
17.
;
18.
;
19.
;
20.
;
21.
;
22.
;
25.
;
26.
;
Задание 1
Вычислить предел:
1.
;
2.
;
3.
;
4.
;
5.
;
6.
;
7.
;
8.
;
9.
;
10.
;
11.
; 12.
;
13.
;
14.
;
15.
;
16.
;
17.
;
18.
;
19.
;
20.
21.
22.
;
23.
;
24.
;
25.
;
26.
;
27.
;
28.
;
29.
;
30.
;
Задание 1.
Вычислить пределы:
1.
;
2.
;
3.
;
4.
;
5.
;
6.
;
7.
;
8.
;
9.
;
10.
;
11.
;
12.
;
13.
;
14.
;
15.
;
16.
;
17.
;
18.
;
19.
;
20.
;
21.
;
22.
;
23.
;
24.
;
25.
;
26.
;
27.
;
28.
;
29.
;
30.
;
Задание 1.
Первоначальный вклад, вложенный в банк под 10% годовых, составил 6 млн. руб. Найти размер вклада через 5 лет при сложном начислении процентов: а) ежеквартальном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 5% годовых, составил 1 млн. руб. Найти размер вклада через 20 лет при сложном начислении процентов: а) каждое полугодие; б) непрерывном.
Первоначальный вклад, вложенный в банк под 4,5% годовых, составил 0,5 млн. руб. Найти размер вклада через 6 лет при сложном начислении процентов: а) каждое полугодие; б) непрерывном.
Первоначальный вклад, вложенный в банк под 6% годовых, составил 2 млн. руб. Найти размер вклада через 10 лет при сложном начислении процентов: а) ежеквартальном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 5% годовых, составил 10 млн. руб. Найти размер вклада через 2 года при сложном начислении процентов: а) каждое полугодие; б) непрерывном.
Первоначальный вклад, вложенный в банк под 8% годовых, составил 3 млн. руб. Найти размер вклада через 4 года при сложном начислении процентов: а) ежеквартальном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 6% годовых, составил 2 млн. руб. Найти размер вклада через 7 лет при сложном начислении процентов: а) ежеквартальном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 9 % годовых, составил 3 млн. руб. Найти размер вклада через 2 года при сложном начислении процентов: а) ежеквартальном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 8 % годовых, составил 4 млн. руб. Найти размер вклада через 3 года при сложном начислении процентов: а) каждое полугодие; б) непрерывном.
Первоначальный вклад, вложенный в банк под 5% годовых, составил 2 млн. руб. Найти размер вклада через 5 лет при сложном начислении процентов: а) ежеквартальном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 4 % годовых, составил 300000 руб. Найти размер вклада через 5 лет при сложном начислении процентов: а) каждое полугодие; б) непрерывном.
Первоначальный вклад, вложенный в банк под 9% годовых, составил 500000 руб. Найти размер вклада через 10 лет при сложном начислении процентов: а) ежеквартальном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 8 % годовых, составил 300000 руб. Найти размер вклада через 12 лет при сложном начислении процентов: а) ежемесячном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 5% годовых, составил 100000 руб. Найти размер вклада через 8 лет при сложном начислении процентов: а) ежемесячном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 4 % годовых, составил 800000 руб. Найти размер вклада через 10 лет при сложном начислении процентов: а) каждое полугодие; б) непрерывном.
Первоначальный вклад, вложенный в банк под 7 % годовых, составил 400000 руб. Найти размер вклада через 3 года при сложном начислении процентов: а) ежемесячном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 10 % годовых, составил 200000 руб. Найти размер вклада через 5 лет при сложном начислении процентов: а) каждое полугодие; б) непрерывном.
Первоначальный вклад, вложенный в банк под 3 % годовых, составил 50000 руб. Найти размер вклада через 5 лет при сложном начислении процентов: а) ежемесячном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 4% годовых, составил 300000 руб. Найти размер вклада через 6 лет при сложном начислении процентов: а) ежемесячном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 4 % годовых, составил 100000 руб. Найти размер вклада через 8 лет при сложном начислении процентов: а) ежеквартальном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 8% годовых, составил 500000 руб. Найти размер вклада через 7 лет при сложном начислении процентов: а) ежемесячном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 4% годовых, составил 100000 руб. Найти размер вклада через 5 лет при сложном начислении процентов: а) каждое полугодие; б) непрерывном.
Первоначальный вклад, вложенный в банк под 6,5% годовых, составил 500000 руб. Найти размер вклада через 4 года при сложном начислении процентов: а) ежемесячном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 9% годовых, составил 400000 руб. Найти размер вклада через 3 года при сложном начислении процентов: а) ежеквартальном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 3% годовых, составил 100000 руб. Найти размер вклада через 10 лет при сложном начислении процентов: а) каждое полугодие; б) непрерывном.
Первоначальный вклад, вложенный в банк под 7% годовых, составил 700000 руб. Найти размер вклада через 4 года при сложном начислении процентов: а) ежемесячном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 9 % годовых, составил 900000 руб. Найти размер вклада через 6 лет при сложном начислении процентов: а) ежеквартальном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 9% годовых, составил 800000 руб. Найти размер вклада через 5 лет при сложном начислении процентов: а) ежемесячном; б) непрерывном.
Первоначальный вклад, вложенный в банк под 5% годовых, составил 200000 руб. Найти размер вклада через 10 лет при сложном начислении процентов: а) каждое полугодие; б) непрерывном.
Первоначальный вклад, вложенный в банк под 6% годовых, составил 400000 руб. Найти размер вклада через 9 лет при сложном начислении процентов: а) ежегодном; б) непрерывном.
Задание 2 Найти производную функций:
1.
;
2.
;
3.
;
4.
;
5.
;
6.
;
7.
; 8.
;
9.
10.
;
11.
; 12.
;
13.
.
14.
;
15.
;
16.
;
17.
;
18.
;
19.
;
20.
;
21.
;
22.
;
23.
;
24.
;
25.
;
26.
;
27.
;
28.
;
29.
;
30.
;
Задание 2.Найти производную функции:
1.
;
2.
;
3.
;
3.
;
5.
;
6.
;
7.
;
8.
;
9.
;
10.
;
11.
;
12.
;
13.
;
14.
;
15.
;
16.
;
17.
;
18.
;
19.
;
20.
;
21.
;
22.
;
23.
;
24.
;
25.
;
26.
;
27.
;
28.
;
29.
;
30.
;
Задание 2.Найти производную функции:
1.
;
2.
;
4.
;
4.
;
5.
;
6.
;
7.
;
8.
;
9.
;
10.
;
11.
;
12.
;
13.
;
14.
;
15.
;
16.
;
17.
;
18.
;
19.
;
20.
;
21.
;
22.
;
23.
;
24.
;
25.
;
26.
;
27.
;
28.
29.
;
30.
;
Задание 3.
Провести полное исследование функции и построить ее график.
1.
;
2.
;
3.
;
4.
;
5.
;
6.
;
7.
;
8.
;
9.
;
10.
;
11.
;
12.;
13.
;
14.
;
15.
;
16.
;
17.
;
18.
;
19.
;
20.
;
21.
;
22.
;
23.
;
24.
;
25.
;
26.
;
27.
;
28.
;
29.
;
30.
;
Задание 4. Вычислить приближенно с помощью дифференциала:
1.
;
x=0,998; 2.
;
x=1,03;
3.
;
x=2,01; 4.
;
x=8,24;
5.
;
x=1,996; 6.
;
x=7,64;
7.
;
x=2,56; 8.
;
x=1,016;
9.
;
x=8,36; 10.
;
x=4,16;
11
;
x=1,012; 12.
;
x=7,76;
13.
;
x=0,98; 14.
;
x=0,08;
15.
;
x=0,97; 16.
;
x=1,97;
17.
;
x=1,021; 18.
;
x=26,46;
19.
;
x=1,012; 20.
;
x=1,21;
21. ; x=27,54; 22. ; x=2,01;
23.
;
x=2,002; 24.
;
x=1,78;
25.
;
x=3,998; 26.
;
x=2,997;
27.
;
x=0,98; 28.
;
x=0,01;
29.
;
x=0,01; 30.
;
x=1,02.