2. Дифракция Френеля на круглом отверстии.

Поставим на пути света от источника непрозрачный экран с круглым отверстием. Дифракционная картина наблюдается на экране, параллельном плоскости отверстия и находящимся от него на расстоянии . Выясним, что будет наблюдаться в точке , лежащей напротив центра отверстия. Отверстие открывает зон Френеля. Зная радиус отверстия можно найти значение : .

Амплитуда результирующего колебания в точке равна:

Если - нечетное, то . Если мало, то и .

Если - четное, .

В общем случае , где знак «+» соответствует нечетным , а «-»- четным.

Если убрать преграду с отверстием, то амплитуда в точке станет равной . Преграда с отверстием, открывающим небольшое нечетное количество зон, ни только не уменьшает освещенность в точке , но напротив приводит к увеличению амплитуды в 2 раза, а интенсивности в 4 раза.

Как видно из формулы число зон Френеля зависит от расстояния экрана до перегородки . Поэтому, перемещая экран, в точке будет наблюдаться то светлое пятно ( - нечетное), то темное ( - четное). Расчет амплитуды колебаний в других точках экрана более сложно.

3. Дифракция Френеля на небольшом диске.

В этом случае диск закрывает первых зон Френеля. Амплитуда результирующего колебания в точке равна:

Итак, в случае диска в точке всегда будет светлое пятно, окруженное концентрическими темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.

Лекция 5 Дифракция Фраунгофера

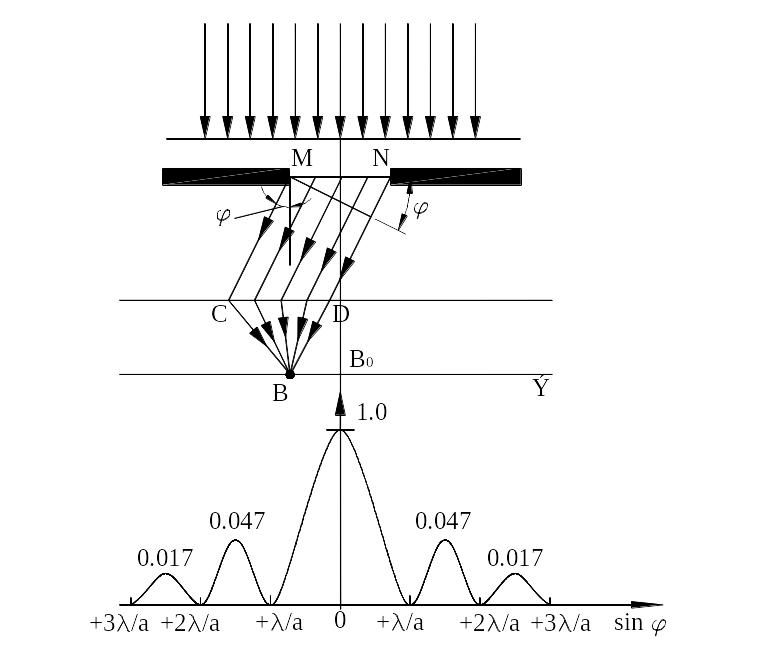
1. Дифракция от одной прямоугольной щели

Для наблюдения дифракции Фраунгофера источник света помещают настолько далеко от щели, что лучи можно считать практически параллельными. На практике источник света располагают в фокусе собирающей линзы, тогда лучи, вышедшие из линзы, будут параллельны (рис. 1).

Рис.1.

Пусть на щель шириной падает монохроматический свет с длиной волны . Из-за дифракции свет после щели распространяется во всех направлениях. Лучи, которые идут не отклоняясь, собираются линзой в точке D (экран находится в фокальной плоскости линзы). Точка D - главный фокус линзы. Рассмотрим лучи, которые дифрагируют под углом . Они соберутся на экране в некоторой точке B (побочном фокусе линзы). Лучи, дифрагирующие под другими углами, соберутся в других точках на экране. В итоге экран будет освещен во многих местах, на нем будет чередование света и тени. Окажется в точке B минимум или максимум зависит от разности хода поступающих сюда волн. Щель является волновой поверхностью. По принципу Гюйгенса каждая точка ее есть источник вторичных волн. Найдем разность хода волн, приходящих в точку B. Для этого проведем фронт волны MF. Точный расчет показывает, что оптические пути MB и FB одинаковы (геометрически путь FB короче, но здесь толще линза). Поэтому разность хода лучей 1 и 2 равна . Проведем систему плоскостей параллельных MF на расстоянии друг от друга. Разность хода разделиться на участки длиной , а щель на полоски, называемые зонами Френеля.

Площади этих зон одинаковы, поэтому по принципу Гюйгенса-Френеля они испускают волны равной интенсивности. Разность хода между соответствующими точками соседних полосок по построению равна . Поэтому, если в щели укладывается четное число зон Френеля, они попарно друг друга погасят. Тогда в точке B будет наблюдаться минимум, если нечетное, то одна зона окажется непогашенной и в точке B будет максимум.

Число зон Френеля равно . Если это число четное, то мы получаем условие минимума:

,

если нечетное, то условие максимума:

.

Величина называется порядком дифракционного спектра.

В направлении наблюдается самый интенсивный центральный максимум нулевого порядка, в этом случае щель действует как одна зона Френеля и интенсивность света велика.

Если на щель падает белый свет, то для каждой длины волны будет соответствовать свой угол и полоски будут окрашены. Ближе к центру будет фиолетовый свет, конец полоски будет красный. Центральный максимум будет общим для всех длин волн, так что центр дифракционной картина будет представляться в виде белой полоски.

Дифракционная картина зависит от соотношения и :

1. Если , то наблюдается описанная дифракционная картина.

2. Если , то в щели укладывается только одна зона Френеля при всех значениях , и на экране будет наблюдаться расплывшийся нулевой максимум.

3. , . Углы будут мало отличаться для малых . На экране будет видно равномерно освещенное изображение щели и только у краев его размытие (при больших значениях ).

От одной щели трудно наблюдать дифракционную картину из-за малой интенсивности. Поэтому обычно используется дифракционная решетка.