5. Качество оценки: коэффициент r2.

Цель регрессионного анализа состоит в объяснении поведения зависимой переменной у. В любой данной выборке у оказывается сравнительно низким в одних наблюдениях и сравнительно высоким — в других. Мы хотим знать, почему это так. Разброс значений у в любой выборке можно суммарно описать с помощью выборочной дисперсии Var (у).

В парном регрессионном анализе мы пытаемся объяснить поведение у путем определения регрессионной зависимости у от выбранной независимой переменной х. После построения уравнения регрессии мы можем разбить значение у_i в каждом наблюдении на две составляющих — и е_i.

y_i = + e_i (2.18)

Величина — расчетное значение у в наблюдении i — это то значение, которое имел бы у при условии, что уравнение регрессии было правильным, и отсутствии случайного фактора. Это, иными словами, величина у, спрогнозированная по значению x в данном наблюдении. Остаток e_i есть расхождение между фактическим и спрогнозированным значениями величины y. Это та часть у, которую мы не можем объяснить с помощью уравнения регрессии. Используя уравнение (2.18), разложим дисперсию у:

Var (y) = Var ( + e ) = Var ( ) + Var(e) + 2Cov ( ,e) (2.19)

Далее, Cov ( ,е) должна быть равна нулю. Следовательно, мы получаем:

Var (y) = Var ( ) + Var (e) (2.20)

Это означает, что мы можем разложить Var (у) на две части: Var ( ) — часть, которая «объясняется» уравнением регрессии в вышеописанном смысле, и Var (е) — «необъясненную» часть.

Согласно (2.20), Var ( )/ Var (у) — это часть дисперсии y, объясненная уравнением регрессии. Это отношение известно как коэффициент детерминации, и его обычно обозначают R ².

(2.21)

что равносильно

(2.22)

Слова «объясненный» и «необъясненный» взяты в кавычки, так как объяснение, в сущности, может быть мнимым. В действительности у может зависеть от какой-то другой переменной z, и х может действовать как величина, замещающая z . Поэтому вместо слова «объясненный» здесь лучше употреблять выражение «представляющийся объясненным».

Максимальное значение коэффициента детерминации равно единице. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, так что = у_i для всех i и все остатки равны нулю. Тогда Var ( ) = Var (у), Var (е) = О и R² = 1.

Если в выборке отсутствует видимая связь между у и х, то коэффициент R² будет близок к нулю.

При прочих равных условиях желательно, чтобы коэффициент R² был как можно больше. В частности, мы заинтересованы в таком выборе коэффициентов а и b, чтобы максимизировать R². Не противоречит ли это нашему критерию, в соответствии с которым а и b должны быть выбраны таким образом, чтобы минимизировать сумму квадратов остатков? Нет, легко показать, что эти критерии эквивалентны, если (2.22) используется как определение коэффициента R². Отметим сначала, что

e_i = y_i - = y_i - a -bx_i (2.23)

откуда, беря среднее значение е_i по выборке и используя уравнение (2.10), получим:

(2.24)

Следовательно,

(2.25) Отсюда следует, что принцип минимизации суммы квадратов остатков эквивалентен минимизации дисперсии остатков при условии выполнения (2.10). Однако если мы минимизируем Var(e), то при этом в соответствии с (2.22) автоматически максимизируется коэффициент R.².

Альтернативное представление коэффициента R²

На интуитивном уровне представляется очевидным, что чем больше соответствие, обеспечиваемое уравнением регрессии, тем больше должен быть коэффициент корреляции для фактических и прогнозных значений y, и наоборот. Покажем, что R² фактически равен квадрату такого коэффициента корреляции между у и , который мы обозначим (заметим, что Cov (е, у) = 0.

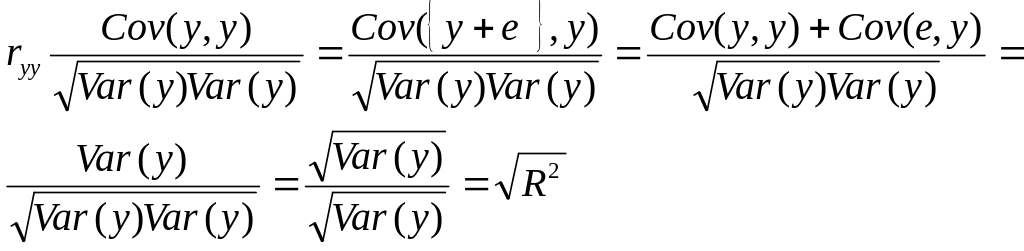(2.26)

Вопросы для повторения

1. Раскройте понятие уравнения регрессии.

2. Что такое «остатки» в регрессионной модели, и каковы причины их существования?

3. Поясните сущность метода наименьших квадратов.

4. Как выглядит система нормальных уравнений в случае парной линейной регрессии?

5. Какие способы определения коэффициента регрессии Вы знаете?

6. Какова интерпретация коэффициента регрессии?

7. Есть ли смысловая интерпретация у свободного члена уравнения парной линейной регрессии?

8. Что показывает коэффициент детерминации?

9. Напишите смысловую формулу коэффициента детерминации.

10. Как связан коэффициент детерминации с линейным коэффициентом корреляции?

1 - доказательство формул (2.9) и (2.10) требует знания основ дифференциального исчисления и здесь не приводится, поэтому принимаем формулы расчета коэффициентов регрессии на веру.

10