
Решение
Для вычислений удобно использовать функцию КПЕР (англ.: NPER), с помощью которой на основе периодических постоянных выплат и постоянной процентной ставки рассчитывается общее количество периодов выплаты.
Для данной задачи по формуле =КПЕР(1%;-100;1000) число выплат равно 11 лет.
Задача 6.
Вас просят дать в долг 15.01.05г. 20000 руб. и обещают вернуть 5000 руб. 11.08.05г., 9000 руб. - 14.12.05г., 7000 руб. - 27.03.06 г. Имеет ли смысл эта сделка при годовой ставке 5%? В каком случае данная сделка является выгодной?
Решение
Решение данной задачи в MS Excel представлено на рис. 9. По результатам решения можно сделать вывод о том, что давать деньги в долг на описанных условиях выгодно, если возвращаемые деньги вкладывать в банк под указанную процентную ставку.
Примечания
Для определения числа дней между двумя датами в обычном (365- или 366-дневном) году нужно вычесть из одной даты другую, при этом каждая дата задается в виде текстового выражения, т.е. в кавычках. Нужно отметить, что при вычитании из более поздней по времени даты более ранней результат представляется положительным числом, а при вычитании из более ранней даты более поздней – отрицательным. Например:
="1.3.2008"-"28.2.2008"(результат равен 2);
="1/1/2005"-"1/1/2004" (результат равен 366);
="31.01.05"-"02.02.05" (результат равен -2).
Начисление сложных процентов при дробном числе лет происходит следующим образом.
- за целое число лет - по формуле сложных процентов
- за дробное число лет - по формуле простых процентов.
Общая формула:
![]() ,
где
,
где
n=a+b – общий срок;
a – целое число;
в – дробное/
Расчет наращенной суммы вклада, если срок финансовой операции задан в днях или месяцах, производится по следующей формуле:
![]() ,
где
,
где
S(0) – первоначальная сумма вклада;
P(n) – наращенная сумма склада;
i – годовая процентная ставка;
t – срок финансовой операции в днях или месяцах;
T – продолжительность года (обозначается в тех же единицах, что и t, и принимает значение =365(366) при точных процентах и =360 при обыкновенных (коммерческих)процентах).
Расчет наращенной суммы вклада при внутригодовом начислении процентов проводится по формуле сложных процентов по подинтервалам и по ставке, пропорциональной доле исходной годовой ставки
![]() ,
где
,
где
S(0) – первоначальная сумма вклада;
P(n) – наращенная сумма склада;
r – годовая процентная ставка;
m – количество начислений в году;
k – количество лет.
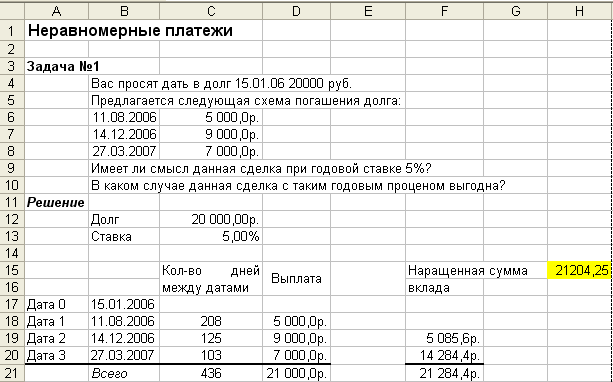
Рис9. Решение задачи 6
В ячейки введены формулы:
Ячейка |
Формула |
Комментарий |
D19 |
=D18*(1+$C$13*(C19/365)) |
Наращенная сумма вклада в размере 5000 руб. |
D20 |
=(D19+F19)*(1+$C$13*(C20/365)) |
Наращенная сумма вкладов в размере 5000 и 9000 руб с процентами за период |
D21 |
=F20+D20 |
Итоговая сумма с выплатой в размере 7000 руб |
Н15 |
=C12*(1+C13)*(1+(71/365)*C13) |
Наращенная сумма вклада при дробном числе лет |
Задача 7.
Предположим, Вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Допустим, Вы собираетесь вложить 1000 руб. при годовой ставке 6%, а затем хотите вкладывать по 100 руб. в начале каждого месяца в течение следующих 12 месяцев. Сколько денег будет на счету в конце этих 12 месяцев?
