6. Второй закон Ньютона. Понятие импульса. Механический принцип относительности.

инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

где  — ускорение материальной точки;  — сила, приложенная к материальной точке; m — масса материальной точки.

Или в более известном виде:

В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил.

где  — импульс точки,

где  — скорость точки;

t — время;  — производная импульса по времени.

Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:

или

Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности.

Нельзя рассматривать частный случай (при ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

7. Третий закон Ньютона. Закон сохранения импульса.

Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.

8. Понятие работы. Вычисление работы переменной силы.

Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины и направления силы (сил) и от перемещения точки (точек) тела или системы

.

Рассмотрим материальную точку, движущуюся под действием силы Р по прямой. Если действующая сила постоянна и направлена вдоль прямой, а перемещение равно s, то, как известно из физики, работа А этой силы равна произведению Ps. Теперь выведем формулу для подсчета работы, совершаемой переменной силой.

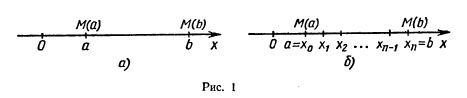
Пусть точка движется по оси Ох под действием силы, проекция которой на ось Ох есть функция f от х. При этом мы будем предполагать, что f есть непрерывная функция. Под действием этой силы материальная точка переместилась из точки М (а) в точку М (b) (рис. 1, а). Покажем, что в этом случае работа А подсчитывается по формуле

(1)

Разобьем отрезок [а; b] на п отрезков одинаковой длины .Это отрезки [а; x₁], [x₁; x₂],..., [x_n-1;b] (рис. 1,6). Работа силы на всем отрезке [а; b] равна сумме работ этой силы на полученных отрезках. Так как f есть непрерывная функция от x, при достаточно малом отрезке [а; x₁] работа силы на этом отрезке приблизительно равна f (а) (x₁—а) (мы пренебрегаем тем, что f на отрезке меняется). Аналогично работа силы на втором отрезке [x₁; x₂] приближенно равна f (x₁) (x₂ — x₁) и т. д.; работа силы на n-ом отрезке приближенно равна f (x_n-1)(b — x_n-1). Следовательно, работа силы на всем отрезке [а; b] приближенно равна:

и точность приближенного равенства тем выше, чем короче отрезки, на которые разбит отрезок [а;b] Естественно, что это приближенное равенство переходит в точное, если считать, что n→∞:

Поскольку A_n при n →∞ стремится к интегралу рассматриваемой функции от а до b, формула (1) выведена.