Стационарные стохастические процессы

Весьма специальный класс стохастических процессов, называемых стационарными процессами, основывается на предположении, что процесс находится в определенном статистическом равновесии. Стохастический процесс называется строго стационарным, если его свойства не зависят от изменения начала отсчета времени. Иными словами, если совместное распределение вероятностей   наблюдений   сделанных в любые моменты времени  , такое же, что и для    наблюдений  , сделанных в соответствующие  моменты времени  . Поэтому, чтобы дискретный процесс был строго стационарным, взаимное распределение любой совокупности наблюдений не должно изменяться при сдвиге всех времен наблюдений вперед или назад на любое целое число  .

Среднее значение и дисперсия стационарного процесса. Когда  , из предположения о стационарности процесса следует, что распределение  вероятности   одинаково для всех времен   и может быть записано как  . Отсюда стохастический процесс имеет постоянное среднее значение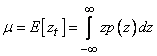 определяющее уровень, относительно которого он флуктуирует, и постоянную дисперсию ,        (2.1.2)

измеряющую его в размерах относительно этого уровня. Поскольку распределение вероятности   одинаково для всех времен  , его форм может быть оценена по гистограмме наблюдений   временного ряда. Кроме того, среднее значение   стохастического процесса можно оценить с помощью выборочного среднего временного ряда

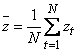,                дисперсию   стохастического процесса – с помощью выборочной дисперсии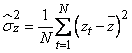 .                          (2.1.4)

 

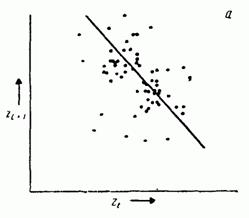
Автоковариация и коэффициенты автокорреляции. Из предположения о стационарности следует также, что совместное распределение вероятностей   одинаково для всех времен  , разделенных одним и тем же интервалом. Следовательно, природу для совместного распределения можно оценить по диаграмме рассеяния, построенной по парам значений   временного ряда, разделенных постоянным интервалом, или задержкой  . Диаграммы рассеяния на рис.2.4 построены по данным циклического процесса. На рис. 2.4,а показаны данные для задержки  (по одной оси отложено  , а по другой  ). На рис. 2.4,б показаны данные для задержки   (по одной оси отложено  , а по другой  ). Мы видим, что соседние значения временных рядов коррелированны; корреляция между   и   отрицательная, а между   и   положительная. Ковариация между значениями   и  , отделенными   интервалами времени, называются автоковариацией с задержкой,   и определяется как

.            (2.1.5)

Аналогично автокорреляция с задержкой   равна

,

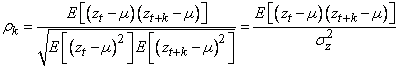поскольку для стационарного процесса дисперсия   в момент времени   та же, что и в момент времени  .Таким образом, автокорреляция с задержкой   равна  ,                                                    (2.1.6)

откуда вытекает, что  .

9. Числові параметри вибірок.

Вибірка — це множина об'єктів, подій, зразків або сукупність вимірів, за допомогою визначеної процедури вибраних з статистичної популяції або генеральної сукупності для участі в дослідженні. Зазвичай, розміри популяції дуже великі, що робить прийняття до уваги всіх членів популяції непрактичним або неможливим. Вибірка представляє собою множину або сукупність певного обсягу, члени якої збираються і статистичні характеристики обчислюється таким чином, що в результаті можна зробити висновки або екстраполяцію із вибірки на всю популяцію або генеральну сукупність.