КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им.А.Н.ТУПОЛЕВА
Институт радиоэлектроники и телекоммуникаций
Кафедра радиоэлектронных и телекоммуникационных систем
В.Р.Линдваль
Метод зеркальных изображений при решении электростатических задач
Учебное пособие к курсовой работе
по дисциплине
«Электромагнитные поля и волны».
Казань, 2004 г.
Содержание
(страницы могут не совпадать)
|
|
Стр. |
|
Введение …………………………………………………………… |
3 |
1. |
Основные положения электростатики …………………………... |
4 |
2. |
Скалярный потенциал электростатического поля .……………… |
5 |
3. |
Метод зеркальных изображений ………………………………..... |
9 |
3.1. |
Заряд у металлической плоскости…………………………………. |
10 |
3.2. |
Заряд в металлическом угле……………………………………..... |
12 |
3.3. |
Заряд у заземлённой металлической сферы……………………… |
14 |
4. |
Программа POLE и работа с ней .…………………………………. |
16 |
4.1. |
Пример 1. Система точечных зарядов…………………………….. |
17 |
4.2. |
Пример 2. Точечные заряды над металлической плоскостью ….. |
19 |
4.3. |
Пример 3. Точечные заряды в металлическом угле……………… |
20 |
4.4. |
Пример 4. Точечные заряды у металлической сферы………….... |
22 |
5. |
Типовые задания на курсовую работу ……………………………. |
24 |
|
Список литературы ……………………………………………….... |
28 |
Введение
При изучении дисциплины «Специальные разделы физики» и, в особенности, при выполнении курсовой работы по ней, студенты сталкиваются с необходимостью выполнения расчётов электростатических полей системы электрических зарядов в присутствии металлических тел. Имеющийся в литературе [1 – 6] материал на эту тему даёт лишь краткие описания методов решения таких задач и не сопровождается программными средствами их решения. Настоящее пособие должно восполнить этот пробел. Кроме основных теоретических положений электростатики и описания метода зеркальных отображений, оно содержит описание программы POLE и примеры её использования при решении ряда задач.
Пособие предназначено для студентов заочной и очной форм обучения специальностей 201000 «Многоканальные телекоммуникационные системы» и 201200 «Средства связи с подвижными объектами», но может быть использовано студентами других специальностей направлений «Телекоммуникации» и «Радиотехника» при изучении стандартных дисциплин дисциплин «Электромагнитные поля и волны», «Электродинамика и распространение радиоволн».
1. Основные положения электростатики
Статические поля
характеризуются постоянством всех
величин во времени
и отсутствием электрических токов
.
При этих условиях система уравнений
Максвелла разделяется на две полностью
независимых системы, одна из которых
,
(1)
(2)
описывает
электростатическое поле. Здесь
-
вектор напряжённости электрического
поля,
-
вектор электрической индукции,
-
объёмная плотность заряда.
При рассмотрении полей в однородных изотропных линейных диэлектриках, в следствие
,
(3)
где
-
абсолютная диэлектрическая проницаемость
среды, уравнение (2) принимает вид
.
(4)
В случае расчёта
поля в вакууме или воздухе
.
В диэлектрике
,
где
-
относительная диэлектрическая
проницаемость.
В проводящей среде
удельная проводимость
.
Из дифференциальной формы закона Ома
и условия отсутствия электрических
токов (плотность тока проводимости
)
следует, что внутри проводящей среды
электростатическое поле отсутствует.
Это значит, что
и, в соответствии с (3)
.
При подстановке последнего в (2) имеем
.
(5)
Это означает, что
внутри проводника нет зарядов. В условиях
электростатики электрические заряды
сосредоточены на поверхности проводника,
где их распределение характеризуется
поверхностной плотностью заряда
.
Если незаряженное проводящее тело помещено в электростатическое поле, то под действием сил поля свободные заряды тела начнут перемещаться. Это перемещение зарядов к поверхности завершится тогда, когда поверхностные заряды полностью компенсируют электрическое поле внутри проводника. Наступит электростатическое равновесие, при котором поверхность тела будет границей электростатического поля в диэлектрике, окружающем проводник.
На границе раздела диэлектрик – проводник граничные условия записываются в виде
,
(6)
.
(7)
Из выражений (6),
(7) следует, что на границе вектор
ориентирован перпендикулярно поверхности
проводника, силовые линии начинаются
на положительных поверхностных зарядах
и оканчиваются на отрицательных
.
2. Скалярный потенциал электростатического поля
Уравнение (1)
представляет собой условие потенциальности
электростатического поля. Действительно,
вследствие тождества
,
электростатическое векторное поле
может быть выражено через скалярную
функцию, называемую скалярным электрическим
потенциалом
.
(8)
Очевидно, что электростатический потенциал определяется с точностью до произвольной постоянной, так как
.
(9)
Подставив (8) в (4), получаем уравнение
,
(10)
называемое скалярным уравнением Пуассона.
В тех областях,
где нет зарядов
,
оно переходит в скалярное уравнение
Лапласа
.
(11)
При распределении
заряда с плотностью
в области V
однородного безграничного диэлектрика
потенциал в некоторой точке
даёт
выражение
,
(12)
где вектор
задаёт
положение точки наблюдения M,
вектор
задаёт
положение точки с зарядом, r
– расстояние между этими точками, а
интегрирование производится по всем
точкам с зарядами (рис.1).
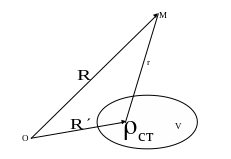
Рис.1. Геометрия задачи
Если размеры объёма V много меньше расстояния от него до точек, где определяется его поле, то его можно считать точечным и имеющим величину заряда
.
(13)
Тогда для точечного заряда, помещённого в начало координат О, имеем
,
(14)
где r – расстояние от заряда до точки наблюдения. Из (14) следует, что поверхности постоянного потенциала (U=const) будут сферами (r=const).
Применив выражение (8), взятое в сферической системе координат, получаем напряжённость электрического поля
,
(15)
где
- орт сферической системы координат.
Определим работу А сил поля при переносе пробного заряда q из точки N в точку M (рис.2)
.
(16)
Рис.2. К определению работы сил поля
Известно, что
,
поэтому
.
(17)
Если принять
,
то выражение (17) определит потенциал
точки М.
Обычно точку N нулевого потенциала размещают в бесконечности или совмещают с корпусом прибора и землёй.
Электростатический потенциал определяется как работа сил поля по переносу положительного единичного точечного заряда из заданной точки в точку нулевого потенциала (в бесконечность).
.
(18)
Если поле создаётся
несколькими точечными зарядами (рис.3),
то вследствие линейности уравнений (1)
и (4) можно использовать принцип
суперпозиции, суммирую потенциалы
зарядов алгебраически, а их поля
электрической напряжённости векторно
Рис.3. Система нескольких точечных зарядов
,
(19)
,
(20)
где
- расстояние от i-го
заряда до точки М,
- орт этого направления.
Очевидно, что расчёты по выражению (19) существенно проще, чем по (20). Полученное в результате скалярное поле потенциала изображают в виде поверхностей постоянного потенциала. В плоском сечении имеем картину линий равного потенциала U=const.
Для плоской задачи (рис.3)
(21)
Вследствие (8) силовые линии вектора в каждой точке перпендикулярны линиям равного потенциала и направлены в сторону убывания потенциала: от положительных зарядов и отрицательным или земле, от земли к отрицательным зарядам.