
§4. Алгебраические операции. Основные типы алгебраических структур
Алгебра − наука об алгебраических операциях. Свойства множеств с алгебраическими операциями изучаются в этом параграфе.
1°. Алгебраические операции.
Пусть X − произвольное множество.
Определение 1.
![]() -арной
алгебраической операцией
на X
называется отображение
-арной
алгебраической операцией
на X
называется отображение
![]() .
То есть
.
То есть
![]() –
компонентному
элементу
–
компонентному
элементу
![]() однозначно ставится в соответствие
элемент
однозначно ставится в соответствие
элемент
![]() .
.
Задача.
Пусть
![]() .
Сколько
.
Сколько
![]() n–арных
алгебраических операций на
n–арных
алгебраических операций на
![]() ?
Ответ. Таких
операций
?
Ответ. Таких
операций
![]()
Алгебраические
операции при
![]() называются унарными,
при
называются унарными,
при
![]() – бинарными,
– бинарными,
![]() – тернарными.
Далее, как правило, будут рассматриваться
бинарные операции.
– тернарными.
Далее, как правило, будут рассматриваться
бинарные операции.
Если
![]() ,
то пишут
,
то пишут
![]() или
или
![]() .
Операции на X
обозначают символами
.
Операции на X
обозначают символами
![]() .
Последний символ используется для
операции сложения, остальные − для
операции умножения.
.
Последний символ используется для
операции сложения, остальные − для
операции умножения.
Определение 2. Множество X с конкретной алгебраической операцией называется алгебраической структурой.
На одном и том же множестве X могут быть заданы различные алгебраические структуры.
Примеры (алгебраических операций и алгебраических структур).
1. (R,
+) − алгебраическая структура, и
![]() R
имеем
R
имеем
![]()
2. (R, -) − алгебраическая структура.
3. (R,
![]() )
− алгебраическая структура.
)
− алгебраическая структура.
4. Деление не
является алгебраической операцией на
R,
так как не определено деление на нуль.
Однако оно является алгебраической
операцией на (R![]() ).
).
5–8. То же самое для С.
9. (Rn, +) − алгебраическая структура.
10. Скалярное произведение не является алгебраической операцией на множестве векторов, так как результатом операции является число.
11.
![]() – множество всех отображений
– множество всех отображений
![]() относительно операции композиции
относительно операции композиции
![]() является алгебраической структурой.
является алгебраической структурой.
12. Как правило,
алгебраическая операция на конечном
множестве может быть задана с помощью
таблицы Кэли, которая описывает результат
операции на любой паре элементов
множества. Рассмотрим множество,
состоящее из 3-х элементов: {Доска, Окно,
Тряпка} (кратко {Д, О, Т}). Введем следующую
операцию, обозначаемую
![]() (символ операции). Соответствующую
таблицу Кэли можно выбрать в виде
(символ операции). Соответствующую
таблицу Кэли можно выбрать в виде
1 |
Д |
О |
Т |
Д |
Д |
О |
Д |
О |
О |
Д |
Т |
Т |
Т |
Т |
Д |
13. Примерами
тернарных операций на
R3
![]() R
R
R
являются:
R
R
R
являются:
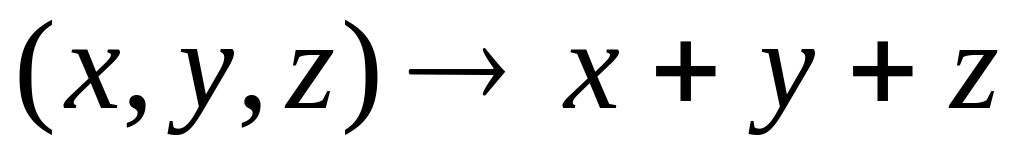 .
.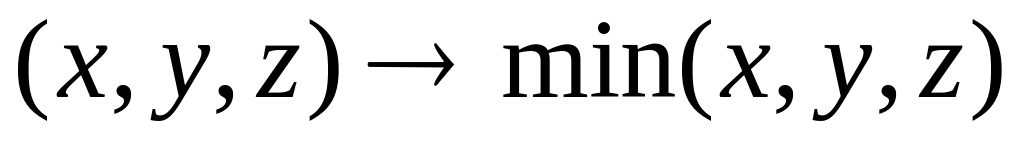 .
.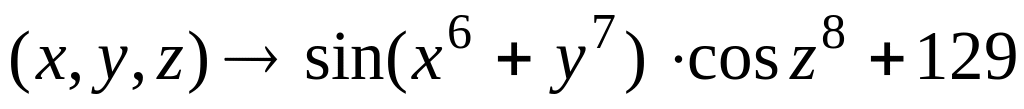 .
.
Обычно рассматривают операции со специальными свойствами.
Определение 3.
Бинарная операция
на X
называется коммутативной,
если
![]() выполняется
выполняется
![]() ;
ассоциативной,
если
;
ассоциативной,
если
![]() выполняется
выполняется
![]() .
.
Замечание.
Если
![]() (то есть множество
конечное) и
− коммутативная операция, то таблица
Кэли симметрична относительно диагонали.
(то есть множество
конечное) и
− коммутативная операция, то таблица
Кэли симметрична относительно диагонали.
Задача.
Пусть
![]() .
Сколько
коммутативных бинарных операций на X?
Ответ.
Таких операций
.
Сколько
коммутативных бинарных операций на X?
Ответ.
Таких операций
![]() .
.
Примеры.
В (R, +) операция сложения коммутативна и ассоциативна.
В (R, -) операция вычитания не коммутативна и не ассоциативна. Например,
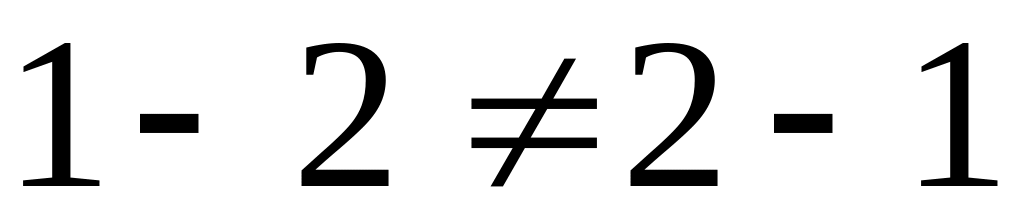 ,
,
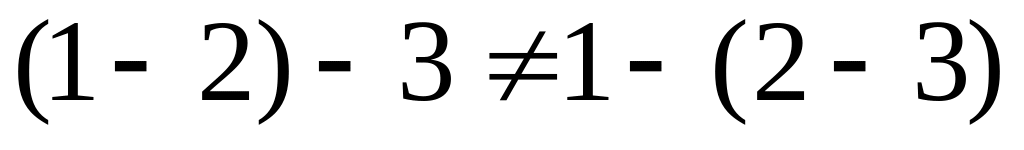 .
.(R,
 ),
где
),
где

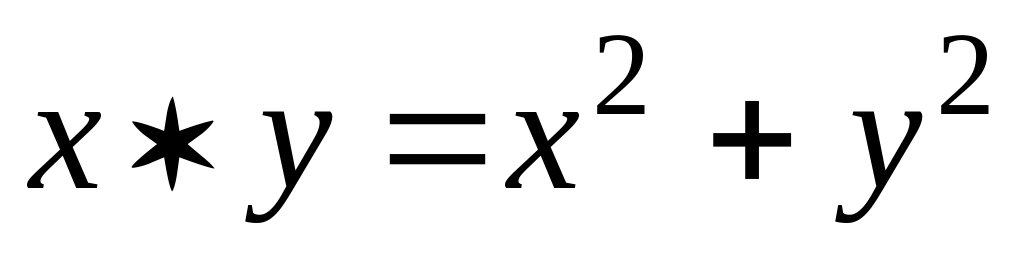 ,
такая операция
коммутативна, но не ассоциативна.
Действительно:
,
такая операция
коммутативна, но не ассоциативна.
Действительно: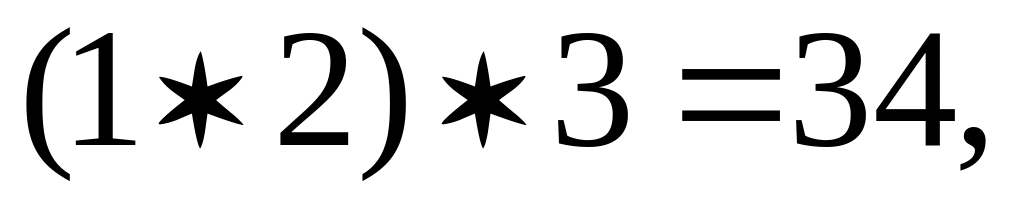
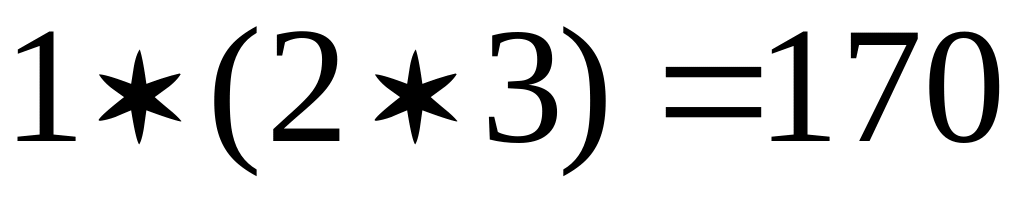 .
.Умножение матриц является ассоциативной, но не коммутативной операцией.
Теорема 1
(обобщённая
ассоциативность). Если операция
ассоциативна,
то в выражении
![]() скобки можно расставлять в любых местах.
скобки можно расставлять в любых местах.
Доказательство.
Проводится методом математической
индукции. Для
![]() утверждение повторяет определение
ассоциативности. Пусть
утверждение повторяет определение
ассоциативности. Пусть
![]() .
Рассмотрим выражения
.
Рассмотрим выражения
![]() и
и
![]() ,
,
в которых выписаны
лишь внешние скобки. Пусть![]() в силу предположения индукции эти
выражения можно переписать в виде
в силу предположения индукции эти
выражения можно переписать в виде
![]()
и
![]() ,
,
или
![]() и
и
![]()
которые равны в силу определения ассоциативности. ■
Определение 4.
Элемент
![]() называется нейтральным относительно
алгебраической операции
,
если
называется нейтральным относительно
алгебраической операции
,
если
|
(1) |
Теорема 2. Нейтральный элемент единственен.
Доказательство.
![]() (от противного). Пусть
(от противного). Пусть
![]() и
и
![]() −
два нейтральных элемента
−
два нейтральных элемента
![]()
![]() (по условию
нейтральности
(по условию
нейтральности
![]() )
и
)
и
![]() (по условию нейтральности
)
(по условию нейтральности
)
![]() .■
.■
Определение 5.
Множество
![]() с
заданной на нем бинарной ассоциативной
операцией называется полугруппой.
Полугруппа с нейтральным элементом
называется моноидом
или полугруппой
с единицей.
с
заданной на нем бинарной ассоциативной
операцией называется полугруппой.
Полугруппа с нейтральным элементом
называется моноидом
или полугруппой
с единицей.
Определение 6.
Элемент
![]() моноида
моноида
![]() называется симметричным к элементу
называется симметричным к элементу
![]() ,
если
,
если
|
(2) |
Теорема 3.
Если в моноиде для
![]() есть
симметричный элемент, то такой элемент
единственен.
есть
симметричный элемент, то такой элемент
единственен.
Доказательство.
Пусть для данного
![]() два симметричных элемента
два симметричных элемента
![]() и
и
![]() Тогда в силу (1) и (2) имеем:
Тогда в силу (1) и (2) имеем:
![]() .■
.■
Обычно умножение
называют мультипликативной
операцией, сложение – аддитивной.
В случае мультипликативной операции
результат операции
![]() называют
произведением,
нейтральный элемент – единицей
(обозначают 1), симметричный элемент к
– обратным
(пишут
называют
произведением,
нейтральный элемент – единицей
(обозначают 1), симметричный элемент к
– обратным
(пишут
![]() ).
В случае аддитивной операции результат
операции
называют суммой
(
).
В случае аддитивной операции результат
операции
называют суммой
(![]() ),
нейтральный – нулём
(обозначают 0), симметричный –
противоположным
(обозначают
),
нейтральный – нулём
(обозначают 0), симметричный –
противоположным
(обозначают
![]() ).
).
Теорема 4.
Если в моноиде
для
элементов
![]() и
и
![]() есть симметричные элементы
есть симметричные элементы
![]() и
и
![]() соответственно, то для элемента
соответственно, то для элемента
![]() также
существует симметричный элемент, равный
также
существует симметричный элемент, равный
![]()
Доказательство.
Для
доказательства теоремы необходимо
проверить условия (2):
![]() Проверим первое из этих равенств. Имеем:
Проверим первое из этих равенств. Имеем:
![]()
Аналогично проверяется второе условие из (2).■

 2
2