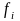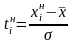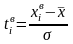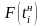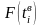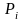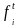7.4. Построение кривой нормального распределения.

Задача: имеется партия деталей, которые должны поставляться в интервале времени с определенной частотой в зависимости от длительности производственного цикла.

Границы интервала, час.	Частота
- - 28 28-113 113-198 198-283 283-368 368-453 453-538 538-623 623-708 708-+	0 5 12 12 15 9 9 7 2 0
Итого:	71

Порядок действий:

- определяем среднее арифметическое и среднеквадратическое отклонение;

- выполнить расчеты для нахождения теоретических частот, где 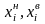нижняя и верхняя граница соответственно, и - значение функции Лапласа в интервале 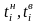. - вероятность попадания в интервал и - частота теоретического распределения.

- , - определяются по таблицам интегрированной функции Лапласа.

- оценка вероятностей попадания случайной величины в интервал определяется разностью .

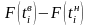- теоретическая частота определяется по формуле: . .

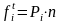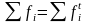7.5. Закон Пуассона (закон редких событий).

При рассмотрении маловероятных событий, которые имеют место в большой серии независимых испытаний некоторое число раз, вероятности появления этих событий подчиняются закону Пуассона или закону редких событий:

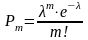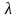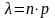, где - равна среднему числу появлений событий А в n одинаковых, независимых испытаниях, т.е. , где 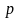- вероятность события при одном испытании, 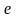=2,71828, 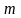- частота данного события. Математическое ожидание

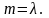
Закон Пуассона можно применять для совокупностей, достаточно больших по объему 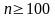. Имеющих достаточно малую долю единиц, обладающих данным признаком .

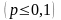Например, количество бракованных деталей, количество отказов автоматических линий и т.д.

Количество бракованных деталей	Наблюдаемая частота	Частота теоретического распределения.
0	604	606
1	306	303
2	77	76
3	12	13
4	1	2
Итого:	1000	1000

Сопоставление наблюдаемых и теоретических частот свидетельствует о достаточном соответствии эмпирического распределения распределению Пуассона.

7.6. Биноминальное распределение

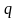Это распределение вероятностей исходов события, которые могут быть классифицированы как положительные и отрицательные: - наступление события, - не наступление события. .

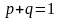Когда существует 2 события: .

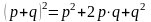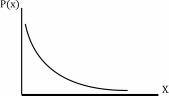
(График представить самостоятельно)

Биноминальное, нормальное, распределение Пуассона считаются главными распределениями и носят прикладной характер.

Тема №8. Критерии согласия.