24.Уравнение линии на плоскости, линии и поверхности в пространстве.

Линия в пространстве:

Точка на плоскости задается парой чисел х и у.

Линия в пространстве задается как пересечение поверхностей.

Пусть L- пересечение поверхностей П1,П2

П1: F1(x;y;z)=0

П2: F2(x;y;z)=0

L: F1(x;y;z)=0

F2(x;y;z)=0

Линия на плоскости->F(х;у)=0

Уравнение F(х;у)=0 называется уравнением линии L, если:

1)координаты любой точки М0 (х0;у0), принадлежащей линии L, являются решением этого уравнения: F(х0;у0)=0(-верное равенство)

И,обратно,

2)если х0;у0 – решение ур-я F(х;у)=0, то точке (х0;у0) принадлежит L.

Точка в пространстве -> (х;у;z)-тройка чисел

Поверхность в пространстве ->F(x;y;z)=0.

Опр.Ур-е F(x;y;z)=0 наз. Ур-ем поверхности П[пи],если:

1)если точка М0 (х0;у0;Z0) принадлежит поверхности П[пи], то х0;у0;Z0- решение этого уравнения и обратного;

2)если числа х0;у0;Z0- это решение этого ур-я, то точка с координатами (х0;у0;Z0) принадлежит поверхности П[пи].

Замечание: М(х;у) – ур-е линии, но она может быть и уравнением плоскости, когда Zне=0

25.Алгебраические линии. Алгебраические поверхности. алгебраические линии первого и второго порядков (эти линии в декартовых прямоугольных координатах определяются соответственно алгебраическими уравнениями первой и второй степени). Первого порядка: Ax + By+ Сz=0., где числа А и В-одновременно не равны 0 Второго порядка: A11x²+2А12ху+А22у² +2В1х+2В2у+С=0. Может быть в виде эллипса, гиперболы, параболы, пары мнимых прямых, паре совпадающих прямых, паре параллельных прямых. алгебраические поверхности первого и второго порядков: алгебраическое уравнение первого порядка: Ax² + By²+ Сz² +d=0. Алгебраическое уравнение второго порядка: Ax² + By²+ Сz² +Dxy+Exz+Fyz+Gx+Hy+Iz+k=0 Могут быть в виде эллипса, гиперболы, параболы,пары прямых (пересекающихся, параллельных или слившихся).

27.Нормальное уравнение прямой OP ^Ox=α OP перпендикулярно l(прямой эль) |OP|=p

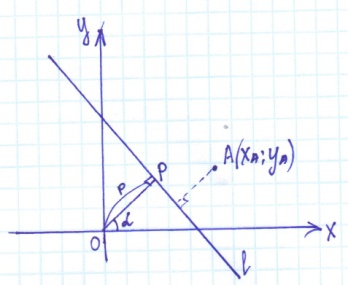l (эль): x*cos α + y*sin α –p =0 d=расстояние от A до l(эль) d=| xA*cos α + yA*sin α –p |

28. Плоскость в пространстве. В трехмерном пространстве в декартовой системе координат любая плоскость описывается линейным уравнением Ax + By + Cz + D = 0,  A² + B² + C² ≠ 0. Это уравнение называется общим уравнением плоскости. Вектор n= (A, B, C) = A·i + B·j + C·k — нормальный вектор плоскости, он перпендикулярен любой прямой, принадлежащей плоскости. Уравнение плоскости, проходящей через точку M₀(x₀,y₀,z₀) перпендикулярно вектору n = (A, B, C) имеет вид A(x −x₀)+ B(y −y₀) + C(z −z₀) = 0. Это уравнение называют уравнением плоскости, проходящей через заданную точку с заданным нормальным вектором. Линейным уравнением относительно переменных x, y, z называется уравнение вида Ax + By + Cz + D = 0, где хотя бы один из коэффициентов А, В, С отличен от нуля. Всякая плоскость в пространстве определяется линейным уравнением Уравнение (4) называется векторным уравнением плоскости.

Пусть   --- какая-нибудь точка плоскости,   --- вектор перпендикулярный плоскости. Тогда уравнение  есть уравнение этой плоскости. Коэффициенты a, b, c, в уравнении плоскости  ax+by+cz+d являются координатами вектора, перпендикулярного плоскости. Если уравнение плоскости разделить на число, равное длине вектора  , то получим уравнение плоскости в нормальной форме. Если же общее уравнение плоскости является полным ( то есть ни один из коэффициентов не равен нулю), его можно привести к виду:

                                    

называемому уравнением плоскости в отрезках. Виды уравнения плоскости в пространстве. Неполные уравнения плоскости. Если хотя бы одно из чисел А, В, С, D равно нулю, уравнение (8.2) называют неполным. Рассмотрим возможные виды неполных уравнений: 1) D = 0 – плоскость Ax + By + Cz = 0 проходит через начало координат. 2) А = 0 – n = {0,B,C} Ox, следовательно, плоскость By + Cz + D = 0 параллельна оси Ох. 3) В = 0 – плоскость Ax + Cz +D = 0 параллельна оси Оу. 4) С = 0 – плоскость Ax + By + D = 0 параллельна оси Оz. 5) А = В = 0 – плоскость Cz + D = 0 параллельна координатной плоскости Оху (так как она параллельна осям Ох и Оу). 6) А = С = 0 – плоскость Ву + D = 0 параллельна координатной плоскости Охz. 7) B = C = 0 – плоскость Ax + D = 0 параллельна координатной плоскости Оуz. 8) А = D = 0 – плоскость By + Cz = 0 проходит через ось Ох. 9) B = D = 0 – плоскость Ах + Сz = 0 проходит через ось Оу. 10) C = D = 0 -  плоскость Ax + By = 0 проходит через ось Oz. 11) A = B = D = 0 – уравнение Сz = 0 задает координатную плоскость Оху. 12) A = C = D = 0 – получаем Ву = 0 – уравнение координатной плоскости Охz. 13) B = C = D = 0 – плоскость Ах = 0 является координатной плоскостью Оуz.