
11.Матричный способ решения систем линейных уравнений .Поскольку обратнуюю матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Существуют системы альфа, бэта и т.д., которые можно заменить матричным уравнением АХ=В, ХА=В. Надо чтобы существовала обратная матрица(это будет когда она невырожденна (это квадратная матрица, определитель которой не =0)) Обратная матрица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E Решение матричных уравнений вида АХ=В и ХА=В. А, В – изв. м-цы; Х-неизв. м-ца
Рассмотрим уравнение АХ=В /*А-1слева или если XA=B то * на А-1справа
А-1(AX)=A-1B
(A-1A)X=A-1B(в силу ассоциативности умножения матриц)
EX=A-1B(по определению обратной м-цы)
X=A-1B
Вывод: Чтобы найти матрицу Х из уравнения АХ=В, надо: 1)найти A-1; 2)умножить м-цу В на А-1 слева.
Аналогично можно получить, что м-ца Х из 2-ого уравнения считается следующим образом: 1)Найти A-1; 2)Умножить В*А-1справа
12.Критерий совместности линейных уравнений Система совместна тогда и только тогда, когда rank A = rank Ā Ответ на вопрос дает теорема Кронекера-Капелли – критерий совместности системы линейных уравнений.
 Теорема.
Система из m
алгебраических уравнений с n
неизвестными имеет решение в том и
только в том случае, когда ранг матрицы
системы равен рангу ее расширенной
матрицы системы(rA =
rĀ ), где
А(αi,j)-матрица
системы, а
Ā=(А/в)-расширенная
матрица системы, в-столбец свободных
членов. Доказательство:
Слова
«в том и только в том случае» означают,
что требуется доказать 2 утверждения(прямое
и обратное). Прямое:
Система имеет решение, следовательно
rA =
rĀ. Обратное:
Если rA =
rĀ , то система
имеет решение. Докажем
прямое утверждение. Обозначим
γ1, γ2, γ3,…,γn
– решение системы. Значит при подстановке
этих чисел вместо неизвестных x1,x2,
x3,
…,xn
соответственно каждое уравнение
образуется в тождество.
Теорема.
Система из m
алгебраических уравнений с n
неизвестными имеет решение в том и
только в том случае, когда ранг матрицы
системы равен рангу ее расширенной
матрицы системы(rA =
rĀ ), где
А(αi,j)-матрица
системы, а
Ā=(А/в)-расширенная
матрица системы, в-столбец свободных
членов. Доказательство:
Слова
«в том и только в том случае» означают,
что требуется доказать 2 утверждения(прямое
и обратное). Прямое:
Система имеет решение, следовательно
rA =
rĀ. Обратное:
Если rA =
rĀ , то система
имеет решение. Докажем
прямое утверждение. Обозначим
γ1, γ2, γ3,…,γn
– решение системы. Значит при подстановке
этих чисел вместо неизвестных x1,x2,
x3,
…,xn
соответственно каждое уравнение
образуется в тождество.
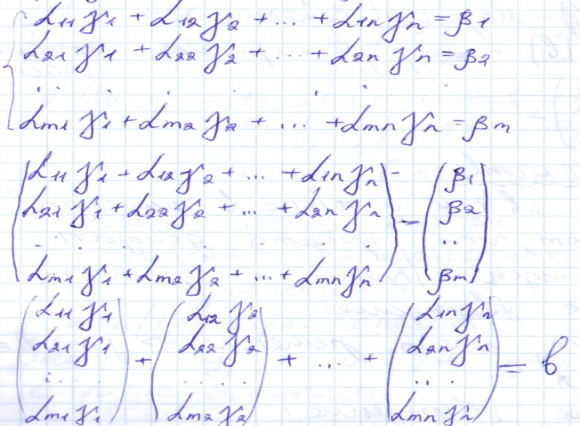 Если
сложить столбцы в левой части этого
равенства, то получится столбец – левая
часть предыдущего равенства. В каждом
столбце можно вынести число γ за скобку.
Если
сложить столбцы в левой части этого
равенства, то получится столбец – левая
часть предыдущего равенства. В каждом
столбце можно вынести число γ за скобку.
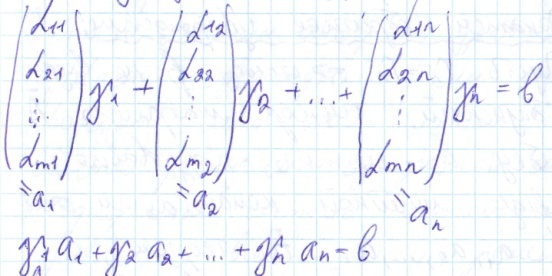
Столбцы а1, а2,…, аn – это столбцы матрицы А. Получили столбец свободных членов в есть линейная комбинация столбцов матрицы А. Значит система столбцов а1, а2,…, аn и столбец в – линейно зависимая система (по 1-му свойству линейно зависимых и линейно независимых систем: «Система столбцов линейно зависима в том и только в том случае, когда хотя бы 1 столбец есть линейная комбинация других столбцов системы».), а ранг матрицы = max числу линейно независимых столбцов, следовательно столбец в не входит в базисный минор матрицы Ā, значит базисный минор матрицы Ā находится в столбцах матрицы А, следовательно rA = rĀ. Докажем обратное утверждение: Пусть rA = rĀ , следовательно столбец в не входит в базисный минор матрицы Ā, следовательно столбец в можно представить в виде линейной комбинации столбцов а1, а2,…, аn.

Это равенство означает, что числа γ1, γ2, γ3,…,γn - это решение системы.
13. Решение систем линейных уравнений методом Гаусса. Метод Гаусса - классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
14.Однородные системы линейных уравнений.
Система линейных алгебраических уравнений называется однородной, если столбец свободных членов этой системы нулевой.
Свойства решений однородной системы: 1)однородная сист. линейных алгебраич. уравнений всегда имеет решение;0,0,…,0-решение однородной системы.
2)Если столбцы у1,у2, решения однородной с-мы,то столбец у1+у2 также является решением с-мы.;
3)Если столбец у-это решение однород.с-мы, то столбец ω (амега)у также является решением этой с-мы.
Однородная система линейных уравнений эквивалентна матричному уравнению Ах=0,где
![]()
Теорема.Однород. сист. линейных алгебраич. уравнений имеет n-r линейно независимых решений
15.Фундаментальная система решений. Любые n-r линейно независимых решений однородной системы называют фундаментальной системой решений (ФСР). Теорема «Общее существование ФСР». Любая однородная система линейных алгебраических уравнений имеет n-r линейно независимых решений, где n-число неизвестных, r-ранг матрицы системы.
16. 1.Геометрическим вектором называется направленный отрезок, который можно перемещать параллельно ему самому. Вектор-множество всех равных друг другу отрезков. Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Векторы а и в называют коллинеарными, если один из отрезков вектора а коллинеарен хотя бы одному из направленных отрезков вектора в. Если угол между векторами равен 90, то векторы называются ортогональными. Направленные отрезки называют сонаправленными если: 1)лежат на параллельных прямых и их концы лежат по 1 сторону от прямой, проходящей через их начало 2)Лежат на 1 прямой и сонаправленны с одним и тем же третьи отрезком. Равные - направленные отрезки, когда они сонаправленны и их длины равны. Отрезок АВ является направленным, если известно какая из 2-х точек А и В является началом отрезка, а какая концом. Направленные отрезки наз.противоположными, если их длины = и они противоположно направлены Длиной вектора а называют длину одного из его направленных отрезков Вектор, состоящий из направленных отрезков, начало и конец которых совпадают, называется нулевым вектором. 2.Линейные операции над векторами Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число 1)Сложение векторов Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b.
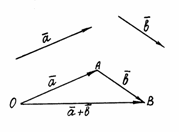
Свойства сложения: (везде вектора) 1.Коммутативность а+в=в+а 2.Ассоциативность (а+в)+с = а+(в+с) 3.нулевой вектор – нейтральный элемент по сложению а+век.0= а; 4. а+(-а)=0 2)Разность векторов. Разностью векторов а и b называется такой вектор с, такой что век.а=век.в+век.с
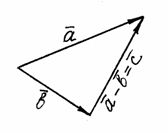
Теорема: Для любых двух векторов существует и притом единственная разность. Доказательство:(над а, в, с -ставить вектора) 1)Пусть даны вектора а и в.Покажем, что с=а+(-в) это разность векторов а и в. Рассмотрим в+с = в+(а+(-в)) = (по свойствам сложения) = в+(-в)+а = 0+а = а, следовательно с = а+в(по определению) 2)
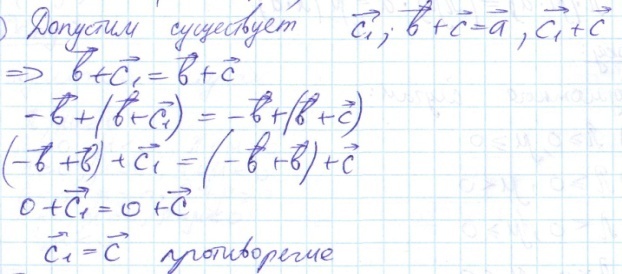
Теорема доказана. 3)Умножение вектора на число Произведением вектора а на число λ называется вектор с, такой что:(над с и а векторы) 1) |с|=|λ|*|а| 2) с↑↑а, если λ >0 c↑↓а, если λ <0 Обозначение: с= λа.
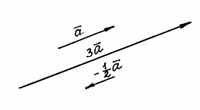
Свойства произведения вектора на число:(над а ставить вектор) Свойство 1. λ*(μ*а) = (λ*μ)*а = μ *(λ*а) Свойство 2. (λ+μ)*а = λ*а+ μ*а Свойство 3. λ*а=0 тогда и только тогда, когда λ=0 либо а=0 Свойство 4.Теорема( критерии коллинеарности векторов) Пусть а не =0 Тогда а↑↑в в том и только в том случае, когда найдется такое число α, что вектор в = α*а. Свойство 5. -а = -1*а Доказательство: Достаточно доказать, что -1*а+а=0 -1*а+а=-1*а+1*а=(-1+1)*а=0 , следовательно -1*а=-а
17. Базис векторов на плоскости и в пространстве. Разложение вектора по базису. БАЗИС В ПРОСТРАНСТВЕ: Базисом в пространстве наз. любые три некомпланарные векторы. Утверждение: Пусть векторы а,в,с – базисы, тогда для любого вектора d найдутся числа α, β, γ, такие что вектор d= α век.а + β век.в.+ γ век.с Базис на плоскости: Базисом на плоскости называют любые 2 неколлинеарных вектора. Пусть векторы а и в - базис. Векторы с, а, в – компланарны (Компланарный вектор – вектор, расположенный в параллельных плоскостях). Существуют α и β, вектор с = α век.а + β век.в (по критерию компланарности). Теорема «Критерий компланарности векторов». Пусть век.а неколлинеарен век.в. Тогда а, в, с компланарны в том и только в том случае, когда найдутся такие числа α и β такие что век.с = α век.а + β век.в.
18. Компонента вектора на прямую, её свойства. Пусть l-прямая, а-вектор
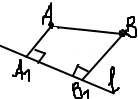 Отложим
вектор а от точки А. Из точек А и В опустим
перпендикуляры на прямую. А1В1-основание
перпендикуляра. век.а’= вектору А1В1
называется компонентой вектора а на
прямую l.
Св-ва компоненты вектора на прямую:
1)(век.а+век.в)’
= век.а’+век.в’. Компонента суммы 2-х
векторов на прямую = сумме компонент
этих векторов на прямую.;
2)(
λ век.а)= λ век.а’
Компонента
произведения вектора на число на
прямую=произведению компоненты вектора
на прямую на это число.
Отложим
вектор а от точки А. Из точек А и В опустим
перпендикуляры на прямую. А1В1-основание
перпендикуляра. век.а’= вектору А1В1
называется компонентой вектора а на
прямую l.
Св-ва компоненты вектора на прямую:
1)(век.а+век.в)’
= век.а’+век.в’. Компонента суммы 2-х
векторов на прямую = сумме компонент
этих векторов на прямую.;
2)(
λ век.а)= λ век.а’
Компонента
произведения вектора на число на
прямую=произведению компоненты вектора
на прямую на это число.
19.Проекция вектора на ось и её свойства. Осью называется прямая с выбранными на ней на ней направлением. Обозначение: ось вектора l [эль] Проекцией вектора а на ось век.l называют длину компоненты век.а на прямую l, взятую со знаком «+», если компонента и ось сонаправленны, и со знаком «-», если противоположно направлены. Обозначение: prвектора l вектора а Свойства проекции: 1)Проекция суммы = сумме проекций prвектора l (век.а+век.в)= prвектора l век. а + prвектора l век.в ; 2) prвектора l (α век.а)= α prвектора l век.а Проекция произведения вектора на число = произведению проекции этого вектора на число.
