8

Показатели вариации

Общее понятие о показателях вариации, их назначение и виды

средняя ве­личина, являясь, по определению, обобщающим показателем для всех единиц ста­тистической совокупности, не дает представления об индивиду­альных значениях варьирующего признака и о различиях между ними. В то же время именно эти различия часто представляют больший интерес для исследователя, так как они позволяют полнее раскрыть строение изучаемой совокупности и получить дополнительный материал для экономико-статистического ана­лиза.

Недостаточность средней величины для исчерпывающей ха­рактеристики совокупности можно проиллюстрировать следую­щим примером. Рассмотрим распределение зданий по количе­ству этажей в двух районах города (табл. 1). Районы А и Б отличаются друг от друга как общей численностью зданий, так и характером их распределения по количеству этажей. В районе А, например доля пятиэтажных зданий составляет 34,9%, а в районе Б - 62,3%. При этом в районе А имеются все виды зданий - от одноэтажных до девятиэтажных, в то время как в районе Б отсутствуют двух- и семиэтажные зда­ния. В то же время среднее количество этажей в одном здании в этих районах одинаково:

Следовательно, в данном случае средняя величина (средняя этажность) не дает представления об особенностях застройки каждого района. Более того, средние этажности районов А и Б обладают разной степенью типичности. В этом легко убедиться, сравнив доли пятиэтажных зданий (вариан­тов, наиболее близких к средней величине) в этих районах. По-видимому, для района Б средняя этажность 5,23 является более характерным показателем, чем для района А. Отсюда вытекает необходимость дополнять средние величины показателями, позволяющими оценить типичность этих средних путем измерения колеблемости (вариации) изучаемого признака. Использование этих показателей вариации дает возможность сде­лать статистический анализ более полным и содержательным и тем самым глубже понять сущность изучаемых общественных явлений.

Простейшим из показателей вариации является размах ва­риации. Он представляет собой разность между наибольшим и наименьшим значениями варьирующего признака:

Этот показатель дает лишь самое общее представление о ко­леблемости изучаемого признака, ибо показывает разницу только между предельными значениями вариантов. Он совер­шенно не связан с частотами в вариационном ряду, т.е. с характером распределения, а его зависимость только от крайних значений признака может придавать ему неустойчивый, слу­чайный характер. В приведенном выше примере эти показатели для обоих районов равны (R_A=9-1=8 и R_Б =9-1=8), сле­довательно, они не дают нам никакой информации об особен­ностях исследуемых совокупностей и не позволяют оценить сте­пень типичности полученных средних.

Из сказанного напрашивается вывод о том, что для харак­теристики вариации признака нужно знать не только ампли­туду (размах) его значений, но и уметь обобщить отклонения всех этих значений от какой-либо типичной для изучаемой совокупности величины. Естественно, в качестве последней уместно использовать среднюю арифметическую. Тогда харак­теристику вариации даст показатель, именуемый средним ли­нейным отклонением и представляющий собой среднюю арифметическую из абсолютных значений отклонений отдельных ва­риантов от их средней арифметической:

(простое); (взвешенное).

Необходимость использования модулей откло­нений вариантов от средней вызвана тем, что алгебраическая сумма этих отклонений равна нулю (см. свойства средней арифметической).

Рассмотрим расчет среднего линейного отклонения в рас­пределениях зданий по количеству этажей (см. табл.1):

Результаты расчета показывают, что вариация зданий по коли­честву этажей в районе Б значительно ниже, чем в районе А, т. е. район Б представляет собой более однородную совокуп­ность зданий, чем район А. Отсюда, кроме того, вытекает, что средняя этажность одного здания 5,23 более типична для района Б, чем для района А ..

Существует и другой способ осреднения отклонений вариан­тов от средней арифметической, позволяющий обойти труд­ность, обусловленную равенством нулю их алгебраической суммы. Этот очень распространенный в статистике способ сво­дится к расчету квадратов отклонений вариантов от средней с их последующим осреднением. При этом мы получаем новый показатель вариации - дисперсию, представляющую собой средний квадрат отклонений вариантов от их средней арифметической:

(простая); (взвешенная).

В экономико-статистическом анализе вариацию признака принято оценивать чаще всего с помощью среднего квадрати­ческого отклонения, представляющего собой корень квадратный из дисперсии:

(простое); 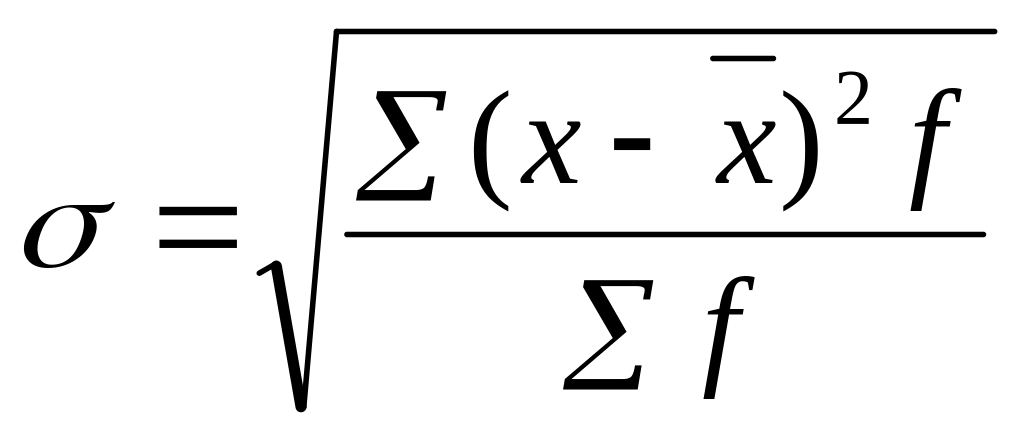(взвешенное).

Среднее квадратическое отклонение, как и среднее линейное отклонение, характеризует абсолютную колеблемость значений варьирующего признака и выражается в тех же единицах из­мерения, что и варианты.

Определим дисперсии и средние квадратические отклонения по нашему примеру:

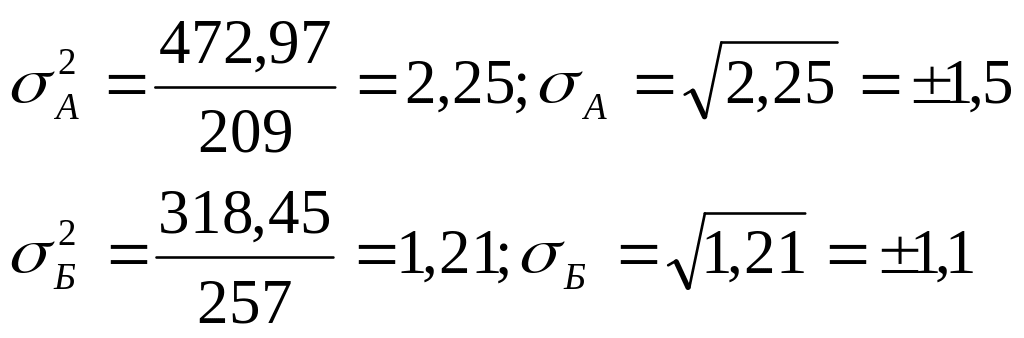
Таким образом, количество этажей в зданиях отклоняется от среднего значения (5,23) на 1,5 этажей в районе А и на 1,1 в районе Б. Этот результат подтверждает сделанный ранее вы­вод о большей однородности застройки района Б по сравнению с районом А.

В статистической практике часто возникает необходимость сравнения вариации различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, количества вносимых в почву удобрений и урожайности и т.д. Для подобных сопоставлений показатели абсолютной колеблемости признаков - среднее линейное и среднее квадратическое отклонение, конечно, не пригодны. Нельзя, в самом деле, сравнивать колеблемость стажа работы, выражаемую в годах, с колеблемостью заработной платы в рублях и копейках.

Для осуществления такого рода сравнений статистика использует относительный показатель вариации - коэффициент вариации, представляющий собой выраженное в процентах (или в виде доли) отношение среднего квадратического отклонения к средней арифметической:

такой показатель мо­жет использоваться для сравнения колеблемости разнородных признаков. Применительно к рассмотренному выше примеру коэффициенты вариации этажности районов А и Б составляют:

Наряду с этим коэффициент вариации часто используется для сравнения размеров вариации в совокупностях, отличаю­щихся друг от друга величиной средней (в совокупностях с разными уровнями).