
Ортогональный план эксперимента
Номер опыта |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
1 |
+1 |
+1 |
+1 |
1- |
1- |
+1 |
… |
+1 |
|
|
|
|
+1 |
+1 |
–1 |
1- |
1- |
–1 |
… |
–1 |
|
|
|
|
+1 |
|
0 |
|
|
0 |
… |
0 |
|
|
|
|
+1 |
0 |
|
0 |
|
0 |
… |
0 |
|
|
|
|
+1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
Таблица 3
Ортогональный план двухфакторного эксперимента
Номер опыта |
|
|||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|||||||||
1 2 3 4 5 6 7 8 9
|
+1 +1 +1 +1 +1 +1 +1 +1 +1 9 |
–1 +1 –1 +1 –1 –1 0 0 0 6 |
–1 –1 +1 +1 0 0 –1 +1 0 6 |
1/3 1/3 1/3 1/3 1/3 1/3 –2/3 –2/3 –2/3 2 |
1/3 1/3 1/3 1/3 –2/3 –2/3 1/3 1/3 –2/3 2 |
+1 –1 –1 +1 0 0 0 0 0 4 |
|
|
|
|
В
первых строчках плана от
![]() до
до
![]() факторы
факторы
![]() ,
составляют различные комбинации значений
+1 и –1. В строчках плана
,
составляют различные комбинации значений
+1 и –1. В строчках плана
![]() каждый фактор последовательно принимает
значения
каждый фактор последовательно принимает
значения
![]() и
и
![]() ,
при этом все остальные факторы равны
нулю. Последовательность постановки
опытов
может быть
случайной.
,
при этом все остальные факторы равны
нулю. Последовательность постановки
опытов
может быть
случайной.
Искомые коэффициенты регрессии определяются соотношением
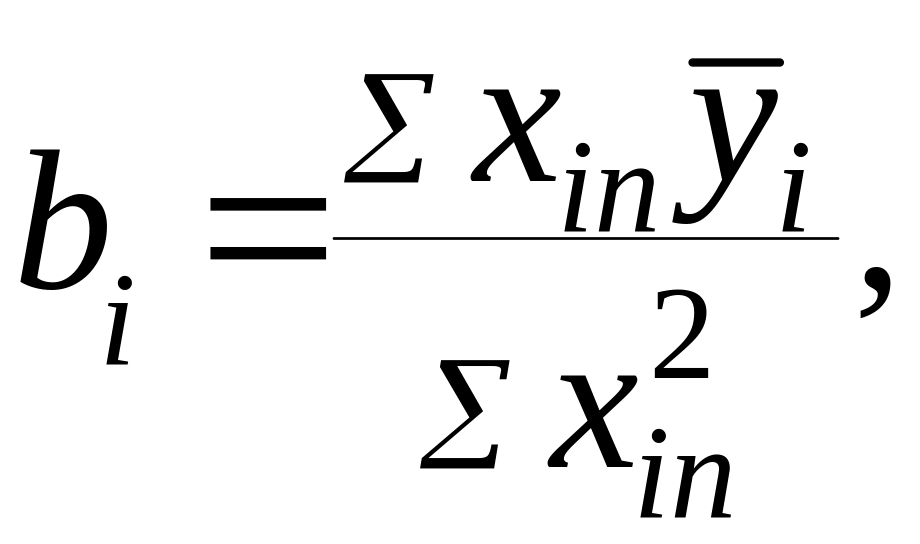
где
![]() – кодированные значения фактора для
столбца, в плане эксперимента,
соответствующего искомому коэффициенту;
– кодированные значения фактора для
столбца, в плане эксперимента,
соответствующего искомому коэффициенту;
![]() – среднее арифметическое значение
искомой величины, полученное по
результатам измерений величин
– среднее арифметическое значение
искомой величины, полученное по
результатам измерений величин
![]()
Далее
вычисляют коэффициент
![]() (
(![]() – значение коэффициента при квадратичных
факторах) и переписывают уравнение
регрессии в виде
– значение коэффициента при квадратичных
факторах) и переписывают уравнение
регрессии в виде
![]() Ошибка
опыта (дисперсия воспроизводимости)
Ошибка
опыта (дисперсия воспроизводимости)
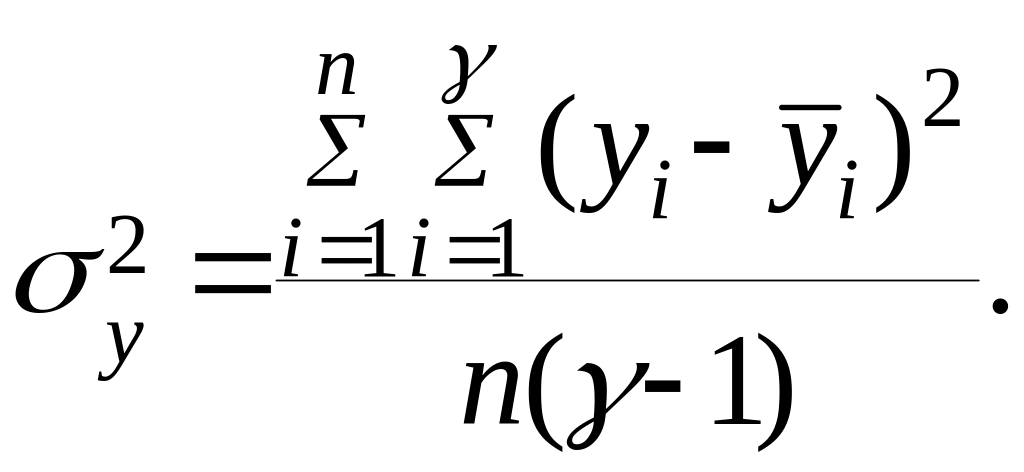
Дисперсия коэффициентов
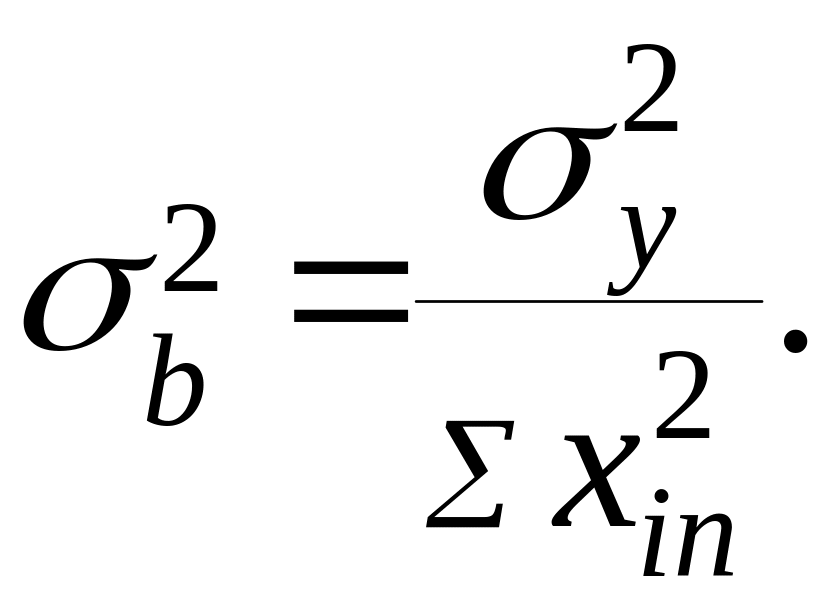
Исходя из этого, определяют значимость коэффициентов, которые должны быть больше действительного интервала их изменения:
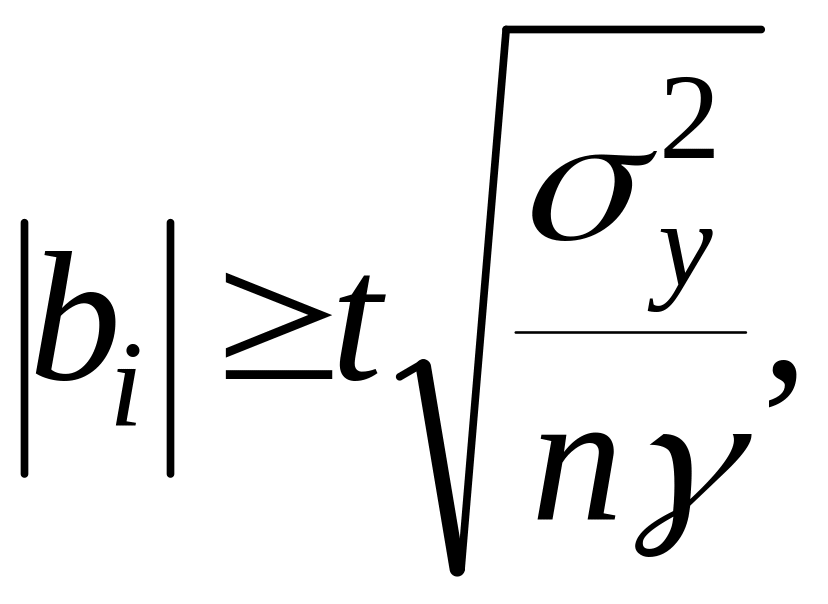
где величина принимается по таблице в зависимости от числа степеней свободы дисперсии воспроизводимости
![]()
Далее проверяют адекватность искомой функции результатам эксперимента.
Дисперсия адекватности
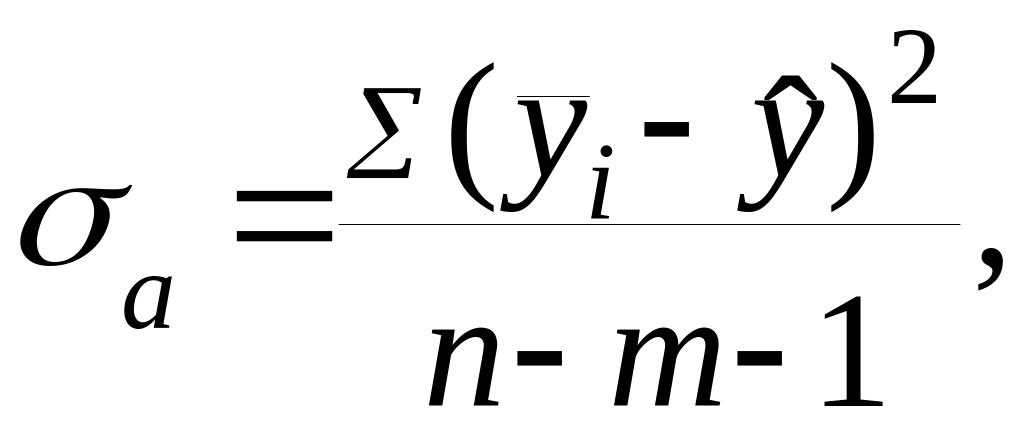
где
![]() – расчетное значение величины,
определяемое по полученной зависимости,
– расчетное значение величины,
определяемое по полученной зависимости,
![]() – число искомых коэффициентов.
– число искомых коэффициентов.
Число степеней свободы дисперсии адекватности
![]()
Адекватность проверяют по критерию Фишера
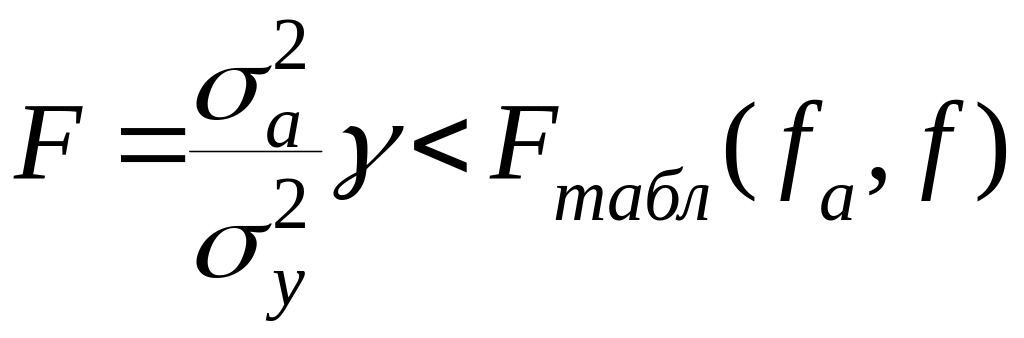 . (2)
. (2)
Далее,
используя соотношения, переходят от
найденного уравнения регрессии в
кодированной форме к искомой зависимости
в натуральных переменных. Если условие
(2) не выполняется, следует перейти к
полиному более высокой степени либо
сузить пределы изменения факторов.
Иногда достаточно найти зависимость в
виде линейного полинома. Здесь
ограничиваются постановкой опытов,
определяемых строчками плана
![]() .
Дальнейшая обработка данных остается
такой же.
.
Дальнейшая обработка данных остается
такой же.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Каким образом оценивается точность измерений?
2. Как определяется результат измерения и его точность?
3. Каким образом определяется необходимое число опытов?
4. Каким образом определяется функциональная зависимость по результатам опытов?
5. Методика построения ортогонального плана эксперимента.
6. Методика определения коэффициентов регрессии и их значимости.
7. Методика проверки адекватности искомой функции результатам эксперимента.
