11.4. Справочный материал :
Задача Штурма-Лиувилля:
- дифференциальное
уравнение
- граничные условия
.
Разыскиваются
значение параметра
(собственные числа), при которых существуют
ненулевые решения дифференциального
уравнения, удовлетворяющие граничным
условиям, а также и сами ненулевые
решения (собственные функции).
Рассматриваются и задачи Штурма-Лиувилля с граничными условиями вида
Смешанная задача для волнового уравнения на отрезке
c
однородными граничными условиями :
- дифференциальное
уравнение
;
- начальные условия
-граничные условия
.
Рассматриваются также однородные граничные условия следующих видов :
Решение этой задачи по методу Фурье получается в виде
где
- собственные функции задача Штурма-Лиувилля
с условиями, соответствующими
рассматриваемым граничным условиям;
- собственные числа
задачи Штурма-Лиувилля;
,
- коэффициенты, определяемые по начальным
условиям.
Смешанная задача для неоднородного волнового уравнения
Ее решение можно получить в виде разложения по собственным функциям задачи Штурма-Лиувилля
где
- решения задачи Коши
коэффициенты
разложений
,
Смешанная задача для уравнения теплопроводности на отрезке с однородными граничными условиями :
- дифференциальное
уравнение
;
- начальное условие
- граничные условия
или одно из
Решение этой задачи по методу Фурье получается в виде
,
где - собственные функции задачи Штурма – Лиувилля с условиями, соответствующими рассматриваемым граничным условиями;
- собственные числа
задачи Штурма-Лиувилля;
- коэффициенты, определяемые по начальным
условиям.
Смешанная задача для неоднородного уравнения теплопроводности
.
Ее решение можно получить в виде разложения по собственным функциям задачи Штурма-Лиувилля
где - решение задачи Коши
- коэффициенты
разложений
Смешанные задачи для волнового уравнения и уравнения теплопроводности с неоднородными граничными условиями
Каждая из этих задач сводится к задаче с однородными граничными условиями для функции
где
Решение получается в виде
Краевая задача для уравнения Лапласа в круговом секторе
(
- полярные координаты,
):
- дифференциальное
уравнение
,
-граничные условия
,
(11.1)
.
(11.2)
Вместо (11.2) рассматриваются и условия
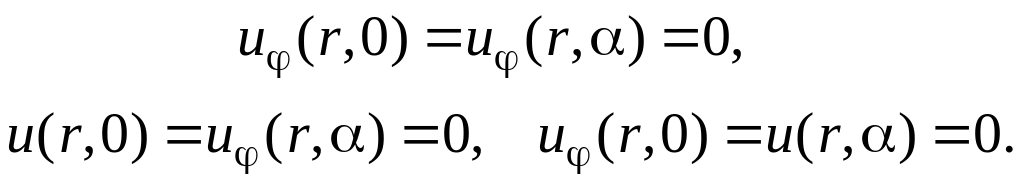(11.3)
Решение задачи по методу Фурье получается в виде
где
- собственные функции задачи Штурма-Лиувилля
для дифференциального уравнения
с условиями, соответствующими рассматриваемым граничным условиям вида (11.2) и (11.3);
- коэффициенты, определяемые по граничным условиям (11.1).
Задача Дирихле для уравнения Лапласа в круге
- полярные
координаты):
- дифференциальное уравнение ;
- граничное условие .
Решение этой задачи по методу Фурье получается в виде
где
- коэффициенты, определяемые по граничным
условиям.