
8. Понятие о напряжениях
Определение 1
♦ Напряжение — численная мера распределения внутренних усилий в сечении или величина внутреннего усилия, действующего в пределах единичной площадки.
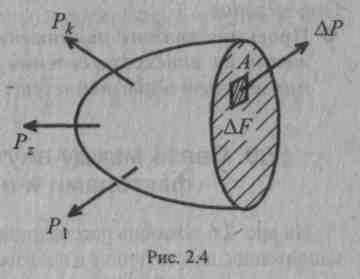
На рис. 2.4 АР— внутреннее усилие, действующее в пределах площадки ΔF.
В соответствии с определением
![]()
где рс—среднее полное напряжение, действующее в пределах площадки ΔF. Очевидно, что напряжение имеет размерность силы, деленной на площадь, т.е. размерность давления (Па, кПа, МПа и т.д.).
Опираясь на гипотезу о сплошности материала твердого тела, осуществим предельный переход
![]()
где р — истинное полное напряжение, действующее в точке А сечения.
В расчетной практике крайне редко работают с полным напряжением. Обычно полное напряжение представляют в виде геометрической суммы его проекций на два взаимно перпендикулярные направления (рис. 2.5).

На рис. 2.5 n — нормаль к плоскости сечения; В — плоскость, содержащая точку А и векторы р и n.
Определение 2
♦ Проекция полного напряжения на нормаль к плоскости сечения называется нормальным напряжением и обозначается σ (сигма).
Определение 3
♦ Проекция полного напряжения на плоскость сечения напряжения на плоскость сечения называется касательным напряжением и обозначается τ (тау).
9. Связь между внутренними силовыми факторами и напряжениями
На рис. 2.6 показана рассматриваемая часть бруса I (см. рис. 2.3) и напряжения, действующие в произвольной точке поперечного сечения.
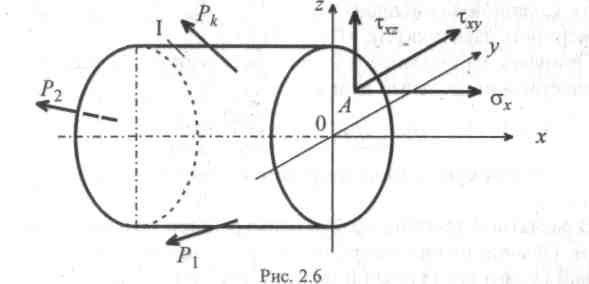
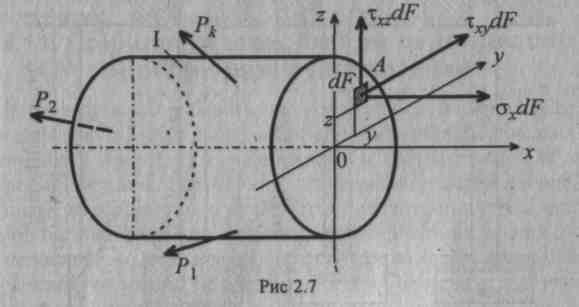
На этом рисунке касательное напряжение представлено в проекциях на координатные направления у и z.
Нормальные и касательные напряжения снабжаются индексами.
Нормальному напряжению присваивается один индекс, соответствующий наименованию оси, которая перпендикулярна сечению и одновременно параллельна линии действия σ.
Касательному напряжению присваиваются два индекса. Первый индекс соответствует наименованию оси, перпендикулярной сечению; второй — наименованию оси, параллельной линии действия данного τ.
На рис. 2.7 показана рассматриваемая часть твердого тела I и усилия, действующие в пределах площадки dF в окрестности точки А.
Вклад усилий σxdF, τxydF и τxzdF, действующих в пределах площадки dF, в величины внутренних силовых факторов составит
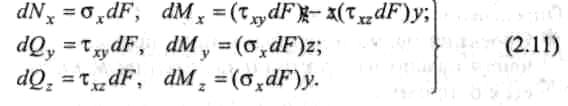
Суммируя эти величины по площади поперечного сечения F, получим окончательно
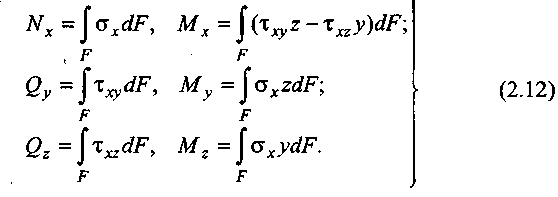
Замечание 2.4
•♦Внутренние силовые факторы NX...MZ и напряжения σ и τ, по существу, представляют собой одно и то же — количественную оценку взаимодействия двух частей твердого тела в данном сечении. Различие состоит в том, что внутренние силовые факторы — интегральная, суммарная оценка этого взаимодействия, а напряжения — локальная, местная оценка.
10. Принцип Сен-Венана
Рассмотрим вопрос о влиянии способа приложения внешней нагрузки на характер распределения внутренних усилий.
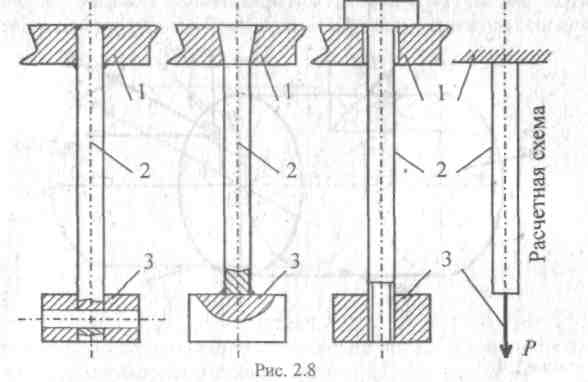
На рис. 2.8 показан стержень, к которому различными способами приложено растягивающее усилие Р.
На рис. 2.8. обозначены: 1 — опорная плита (на расчетной схеме — опора); 2 — растягиваемый стержень; 3 — груз весом Р (на расчетной схеме внешнее усилие Р).
Кроме показанных на рис. 2.8, можно предложить множество иных способов передачи стержню усилия Р. Казалось бы, все эти случаи необходимо рассматривать раздельно. Однако, как показывают расчеты точными методами теории упругости, результаты которых проверены и подтверждены экспериментально, способ приложения внешнего усилия оказывает существенное влияние на закон распределения внутренних усилий лишь в сечениях, достаточно близких к тем, в которых приложены внешние усилия.
(Рассмотрев множество подобных примеров, французский ученый Барре де Сен-Венан (1797—1886) сформулировал принцип, носящий его имя.
♦ Принцип Сен-Венана. В сечениях, достаточно удаленных от точек приложения внешних усилий, закон распределения внутренних усилий (напряжений и деформаций) не зависит от способа приложения внешних усилий.
В курсе сопротивления материалов принято считать, что способ приложения внешних усилий влияет на закон распределения внутренних усилий на расстоянии не более одного характерного размера поперечного сечения стержня от точки приложения внешнего усилия. Поскольку это расстояние достаточно мало по сравнению с длиной стержня (по определению понятия «стержень»), то в курсе сопротивления материалов наличием особых зон (зон Сен-Венана) пренебрегают. По этой причине для всех трех схем передачи стержню растягивающего усилия Р и предложена единая расчетная схема (рис. 2.8).
В зонах, примыкающих к точкам приложения внешних усилий (зонах Сен-Венана), напряжения и деформации определяют точным и методами математической теории упругости. Методы и расчетные соотношения сопротивления материалов в этих зонах дают весьма существенные погрешности.
Особенно важно помнить о наличии зон Сен-Венана при экспериментальных исследованиях, связанных с определением напряжений и деформаций в конструктивных элементах.
